This chapter introduces the fundamental concepts of physical quantities and the importance of measurement in science. It begins by defining what a physical quantity is – something that can be measured (like length, mass, time, temperature, etc.). The chapter emphasizes the difference between physical quantities and non-physical concepts.
Next, it delves into the concept of units. It explains that to express a measurement meaningfully, we need a standard unit. The chapter likely introduces the SI (International System of Units), which is the globally accepted system. Common SI units for basic quantities like meter (m) for length, kilogram (kg) for mass, second (s) for time, and kelvin (K) for temperature are usually covered.
The chapter then moves on to discuss the need for accurate measurement and the instruments used for measuring different physical quantities. This section typically includes:
- Length: Introduction to measuring length using a ruler or measuring tape, emphasizing proper alignment and reading techniques to minimize errors.
- Mass: Explanation of mass as the amount of matter and the use of a beam balance or electronic balance for its measurement.
- Time: Introduction to units of time (seconds, minutes, hours) and the use of clocks and stopwatches for measuring time intervals.
- Temperature: Defining temperature as the degree of hotness or coldness and introducing the Celsius scale as the common unit at this level. The use of a liquid-in-glass thermometer is usually explained.
The chapter might also touch upon the importance of recording measurements with correct units and the idea of estimation before actual measurement as a way to check for reasonableness. It may also briefly introduce the concept of errors in measurement and the need to minimize them through careful techniques.
In essence, this chapter lays the groundwork for understanding the language of physics by introducing the basic measurable quantities, their standard units, and the tools used to measure them accurately. It highlights the fundamental role of measurement in scientific investigation.
Test Yourself
A. Objective Questions
1. Write true or false for each statement
(a) The S.I. unit of volume is litre.
Ans:
False. The standard International System of Units (S.I.) unit for volume is the cubic meter (m³). The litre (L) is a widely used unit for volume, but it is considered a derived unit and not the fundamental S.I. unit.
(b) A measuring beaker of capacity 200 ml can measure only the volume. 200 ml of a liquid.
Ans: True.
(c) cm2 is a smaller unit of area than m2.
Ans: True.
(d) Equal volumes of two different substances have equal masses.
Ans: False.
Equal volumes of two different substances do not necessarily have equal masses. This is because different substances have different densities. Density is the mass of a substance per unit volume. If two substances have different densities, then the same volume of each substance will have different masses.
(e) The S.I. unit of density is g cm-3.
Ans: False.
The correct S.I. unit for density is kilogram per cubic meter (kg/m³).Gram per cubic centimeter (g cm⁻³) is a unit of density, but it belongs to the CGS (centimeter-gram-second) system, not the S.I. system. While g cm⁻³ is often convenient for certain applications, the S.I. standard is kg/m³.
For reference, 1 g/cm³ is equal to 1000 kg/m³.
(f) 1 g cm-3 = 1000 kg m-3.
Ans: True.
(g) The density of water is maximum at 4°C.
Ans: True.
(h) The speed 5 ms-1 is less than 25 km h-1.
Ans: True.
(i) The S.I. unit of speed is ms-1.
Ans: True
2. Fill in the blanks
(a) l m3 = ______ cm3
Ans: 106
(b) The volume of an irregular solid is determined by the method of _______________ .
Ans: displacement of liquid.
(c) Volume of a cube = _________
Ans: (one side)
(d) The area of an irregular lamina is measured by using a _________.
Ans: graph paper.
(e) Mass = density × ___________ .
Ans: volume.
(f) The S.I. unit of density is kg m-3.
Ans: kg m-3.
(g) 1 g cm-3 = ___________ kg m-3.
Ans: 1000
(h) 36 km h-1 = _____ ms-1.
Ans: 10
(i) Distance travelled d = ________ × time t.
Ans: speed v
3. Match the following

4. Select the correct alternative
(a) One litre is equal to :
- 1 cm-3
- 1 m3
- 10-3 cm3
- 10-3 m3
(b) A metallic piece displaces water of volume 15 ml. The volume of piece is :
- 15 cm3
- 15 m3
- 15 × 103 cm3
- 15 × 103 cm3
(c) A piece of paper of dimensions 1.5 m x 20 cm has area :
- 30 m2
- 300 cm2
- 0.3 m2
- 3000 m3
(d) The correct relation is :
- d = M × V
- M = d × Y
- V = d × M
- d = M + V
(e) The density of alcohol is 0.8 g cm-3. In S.I. unit, it will be :
- 0.8 kg m-3
- 0.0008 kg m-3
- 800 kg m-3
- 8 x 103 kg m-3
(f) The density of aluminium is 2.7 g cm-3 and of brass is 8.4 g cm-3. For the same mass, the volume of:
- both will be same
- aluminium will be less than that of brass
- aluminium will be more than that of brass
- nothing can be said.
(g) A block of wood of density 0.8 g cm-3 has a volume of 60 cm3. The mass of block will be :
- 60.8 g
- 75 g
- 48 g
- 0.013 g
(h) The correct relation for speed is
- Speed = distance x time
- speed = distance / time
- speed = time / distance
- speed = 1 / distance x time
(i) A boy travels a distance 150 m in 1 minute. His speed is
- 150 m s-1
- 2.5 m s-1
- 25 m s-1
- 9 m s-1
B. Short/Long Answer Questions
Question 1.
Define the term volume of an object.
Ans:
Volume refers to the measure of the space an object occupies in three dimensions. It indicates how much space is contained within the boundaries of an object. In the case of solid items, volume reflects the space filled by the material they are made of. For hollow objects or containers, it describes how much material or substance they can contain. The cubic meter (m³) is the standard unit used to express volume.
Question 2.
State and define the S.I. unit of volume.
Ans:
The cubic meter is defined as the volume occupied by a cube whose edges are each one meter in length. Imagine a box that is exactly one meter long, one meter wide, and one meter high; the space inside this box is one cubic meter. While the liter (L) is a common unit for volume, it’s equivalent to a cubic decimeter (dm³) and is a derived unit, not the fundamental S.I. unit. One cubic meter contains 1000 liters.
Question 3.
State two smaller units of volume. How are they related to the S.I. unit?
Ans:
Two smaller units of volume are:
- Cubic centimeter (cm³): This is the volume of a cube with sides each measuring one centimeter (1 cm x 1 cm x 1 cm).
- Cubic decimeter (dm³): This is the volume of a cube with sides each measuring one decimeter (1 dm x 1 dm x 1 dm).
Their relationship to the S.I. unit (cubic meter):
- Cubic centimeter (cm³):
- 1 meter (m) = 100 centimeters (cm)
- Therefore, 1 cubic meter (m³) = (100 cm) x (100 cm) x (100 cm) = 1,000,000 cm³
- Conversely, 1 cm³ = 1 x 10⁻⁶ m³
- Cubic decimeter (dm³):
- 1 meter (m) = 10 decimeters (dm)
- Therefore, 1 cubic meter (m³) = (10 dm) x (10 dm) x (10 dm) = 1,000 dm³
- Conversely, 1 dm³ = 1 x 10⁻³ m³
It’s also worth noting that 1 cubic decimeter (dm³) is equal to 1 liter (L), which is a commonly used non-SI unit of volume. So, 1 L = 10⁻³ m³.
Question 4.
How will you determine the volume of a cuboid ? Write the formula you will use.
Ans:
To find the volume of a cuboid, you’ll need to measure its length (l), breadth (b), and height (h). With these measurements, you can easily calculate the volume using the following formula:
Volume (V) = length × breadth × height
Or, expressed symbolically:
V = l × b × h
Where:
- V stands for the volume of the cuboid.
- l represents the length of the cuboid.
- b denotes the breadth (or width) of the cuboid.
- h indicates the height (or thickness) of the cuboid.
It’s crucial to ensure that all three dimensions (length, breadth, and height) are in the same unit of measurement before performing the multiplication. The final volume will then be expressed in cubic units corresponding to the units used for the dimensions (e.g., m³ if the dimensions were in meters, cm³ if in centimeters, and so on).
Question 5.
Name two devices which are used to measure the volume of an object. Draw their neat diagrams.
Ans:
two common devices used to measure the volume of an object are:
- Graduated Cylinder:
Graduated Cylinder for measuring volume
- A graduated cylinder is a tall, cylindrical container with markings along its side indicating volume measurements.
- It’s used to measure the volume of liquids accurately.
- To measure the volume of an object, you can use the water displacement method:
- Fill the graduated cylinder with a known volume of water.
- Carefully submerge the object completely in the water.
- Note the new water level.
- Measuring Beaker:
Measuring Beaker for measuring volume
- A measuring beaker is a wide, cylindrical container with a spout for pouring.
- It has markings on the side to indicate approximate volume measurements.
- While less precise than a graduated cylinder, it’s useful for rough estimates and for mixing liquids.
- Similar to the graduated cylinder, you can use the water displacement method with a beaker to determine the volume of an object.
Question 6.
How can you determine the volume of an irregular solid (say a piece of brass) ? Describe in steps with neat diagrams.
Ans:
To find the volume of an irregular solid like a piece of brass, you can use the displacement method with a graduated cylinder. Here are the steps:
Steps:
Take a graduated cylinder: Choose a graduated cylinder that is wide enough to fit the brass piece and has clear volume markings.
|——————-|
| |
| _______ |
| / \ |
| | | |
| \_______/ |
| | |
| | |
|——–|———-| <– Volume markings
| |
———————
1. Pour water and note the initial volume (V1): Carefully pour some water into the graduated cylinder. Make sure the water level is high enough to completely submerge the brass piece later. Read the water level at the bottom of the meniscus (the curved surface of the water). Record this initial volume (V1).
|——————-|
| |
| _______ |
| / \ |
| | o | | <– ‘o’ represents air bubble (avoid)
| \ /\_\ / | <– Meniscus
| \/ \/ |
|——–V———-| <– Read volume here (V1)
| |
———————
2. Carefully submerge the brass piece: Gently lower the piece of brass into the graduated cylinder containing the water. Ensure that the brass piece is fully submerged and doesn’t touch the sides of the cylinder. You can tie a thread around the brass and use it to lower it slowly to avoid splashing.
|——————-|
| |
| _______ |
| / \ |
| | /\_/\ | | <– Brass piece
| \ ( o.o ) / |
| \/ > ^ <\/ |
|——–/\/\/\——| <– New water level
| |
———————
1. Note the final volume (V2): Once the brass piece is completely submerged and the water level has settled, read the new water level at the bottom of the meniscus again. Record this final volume (V2).
|——————-|
| |
| _______ |
| / \ |
| | | |
| \_______/ |
|——–V———-| <– Read volume here (V2)
| /\_/\ |
| ( o.o ) |
| > ^ < |
———————
2. Calculate the volume of the brass piece: The volume of the irregular solid (brass piece) is the difference between the final volume (V2) and the initial volume (V1).
Volume of brass = V2 – V1
The unit of the volume will be the same as the unit of the markings on the graduated cylinder (usually milliliters or cubic centimeters).
This method works because when the irregular solid is submerged in the water, it displaces a volume of water equal to its own volume. By measuring the change in the water level, you can determine the volume of the solid.
Question 7.
You are required to take out 200 ml of milk from a bucket full of milk. How will you do it ?
Ans:
To take out approximately 200 ml of milk from a full bucket without a precise 200 ml measure, find a clean container with a known volume close to it (like a standard measuring cup or a smaller cup). If it’s slightly larger (e.g., 240 ml), estimate and pour a bit less than full. If smaller (e.g., 100 ml), fill it twice. For a container that’s a multiple (e.g., 400 ml), fill it halfway. If no marked container is available, visually estimate the amount, similar to a small glass. Remember cleanliness is key, and the result will be an approximation unless a precise measuring tool is used. Consider the purpose; if exactness is crucial, a proper measuring device is recommended.
Question 8.
Describe the method in steps to find the area of an irregular lamina using a graph paper.
Ans:
To find the area of an irregular shape using graph paper, first, place the shape on the paper and trace its outline. Then, count all the squares fully inside the outline. Next, count the squares that are more than half inside. Ignore the squares that are less than half inside. The approximate area is the sum of the fully enclosed squares and the more than half enclosed squares, multiplied by the area of one small square on the graph paper. For example, if each square is 1 cm x 1 cm, the total count gives the area in cm². Smaller squares on the graph paper will provide a more accurate measurement.
Question 9.
Define the term density of a substance.
Ans:
Density is a fundamental physical property that quantifies the concentration of mass within a given volume. Essentially, it measures how tightly matter is packed together in a substance.
Defining Density
The relationship is mathematically expressed as:
Density(ρ)=Volume(V)Mass(m)
- Mass (m): The amount of matter in the object (typically measured in kilograms, g, or lbm).
- Volume (V): The space occupied by the object (typically measured in meters3, cm3, or liters).
The standard unit for density is kilograms per cubic meter (kg/m3), though grams per cubic centimeter (g/cm3) is commonly used, especially for liquids and solids .
Conceptual Understanding
Imagine two identical boxes:
- Box A is filled with feathers.
- Box B is filled with rocks.
Both boxes occupy the same volume. However, Box B contains significantly more mass (rocks) squeezed into that space than Box A (feathers).
Therefore, the material in Box B (rocks) has a higher density than the material in Box A (feathers). Density serves as a metric for comparing different materials based on how much “heaviness” they contain per unit of spatial size. This property dictates whether an object will float or sink in a fluid, as well as its behavior in various physical processes.
Question 10.
State the S.I. and C.G.S. units of density. How are they inte related ?
Ans:
S.I. Unit: Kilogram per cubic meter (kg/m³)
C.G.S. Unit: Gram per cubic centimeter (g/cm³)
Interrelation:
1 g/cm³ = 1000 kg/m³
1 kg/m³ = 0.001 g/cm³
Question 11.
‘The density of brass is 8.4 g cm’3’. What do you mean by the statement ?
Ans:
Density (ρ) is the ratio of a substance’s mass (m) to its volume (V) , expressed mathematically as ρ=m/V.
Interpretation of the Value
A density value of 8.4 grams per cubic centimeter means that for any given quantity of pure brass:
- Mass per Unit Volume: Precisely 8.4 grams of mass is contained within every 1 cubic centimeter of space occupied by the material.
- Concentration of Matter: It quantifies how tightly the brass’s constituent atoms (copper and zinc) are packed together. A higher density indicates a greater concentration of matter in a fixed volume, suggesting that brass is a relatively heavy material compared to substances like water (1.0 g cm−3) or aluminum (2.7 g cm−3).
In practical terms, if you were to measure a brass object with a volume of 10 cm3, its total mass would be 10 cm3×8.4 g cm−3=84 grams. Density thus serves as a consistent identifier for brass, independent of the size or shape of the sample.
Question 12.
Arrange the following substances in order of their increasing density:
(a) iron
(b) cork
(c) brass
(d) water
(e) mercury
Ans:
b<a<c<d<e
Question 13.
How does the density of water changes when :
(a) it is heated from 0°C to 4°C,
(b) it is heated from 4°C to 10°C ?
Ans:
Briefly:
(a) 0°C to 4°C: Density rises (due to volume shrinkage).
(b) 4°C to 10°C: Density falls (due to volume expansion).
Explanation:
Water’s density changes uniquely with temperature. From 0°C to 4°C, it shrinks in volume upon heating, causing its density to increase, peaking at 4°C. Beyond this point, from 4°C to 10°C, water behaves typically, expanding in volume as temperature rises, which leads to a decrease in its density. This unusual characteristic, known as the anomalous expansion of water, results in water being densest at 4°C.
Question 14.
Write the density of water at 4°C.
Ans:
The density of water is at its maximum at 4°C. Its value is:
- 1000 kg/m³ (in S.I. units)
- 1.0 g/cm³ (in C.G.S. units)
Question 15.
Explain the meaning of the term speed.
Ans:
Speed is how fast something moves, calculated by the distance it covers divided by the time it takes. It’s just a number (magnitude) without direction.
Question 16.
Write the S.I. unit of speed.
Ans:
The S.I. unit of speed is the meter per second (m/s).
Question 17.
A car travels with a speed 12 m s”1, while a scooter travels with a speed 36 km h-1. Which of the two travels faster ?
Answer:
To compare the speeds, we need to have them in the same unit. Let’s convert the speed of the scooter from km/h to m/s.
To convert km/h to m/s, we multiply by 3600 s1000 m or simplify it to 185.
Speed of the scooter = 36 km/h×185
Speed of the scooter = 2×5 m/s
Speed of the scooter = 10 m/s
Now we can compare the speeds:
- Speed of the car = 12 m/s
- Speed of the scooter = 10 m/s
Since 12 m/s is greater than 10 m/s, the car travels faster.
Final Answer: The final answer is Car
C. Numericals
Question 1.
The length, breadth and height of a water tank are 5 m, 2.5 m and 1.25 m respectively. Calculate the capacity of the water tank in (a) m3 (b) litre.
Ans:
To determine the capacity of the rectangular water tank, we must first calculate its volume using the formula for a cuboid: V=l×b×h.
(a) Capacity in Cubic Meters (m3)
Given the dimensions of the tank:
- Length (l) =5 m
- Breadth (b) =2.5 m
- Height (h) =1.25 m
The volume calculation is:
Volume (V)=5 m×2.5 m×1.25 m
V=12.5 m2×1.25 m
V=15.625 m3
Thus, the capacity of the water tank in cubic meters is 15.625 m3.
(b) Capacity in Litres
To convert the volume from cubic meters to litres, we use the standard conversion factor:
1 m3=1000 litres
Multiplying the volume in m3 by 1000 gives the capacity in litres:
Capacity in litres=15.625 m3×1000m3litres
Capacity in litres=15625 litres
The capacity of the water tank in litres is 15625 litres.
Final Capacity:
- 15.625 m3
- 15625 litres
Question 2.
A solid silver piece is immersed in water contained in a measuring cylinder. The level of water rises from 50 ml to 62 ml. Find the volume of silver piece.
Ans:
The volume of the silver piece can be determined by the displacement of water in the measuring cylinder.
- Initial volume of water (V1) = 50 ml
- Final volume of water after immersing the silver piece (V2) = 62 ml
The volume of the silver piece is equal to the difference between the final and initial volumes of water.
Volume of silver piece = V2 – V1
Volume of silver piece = 62 ml – 50 ml
Volume of silver piece = 12 ml
Since 1 ml is equal to 1 cm³, the volume of the silver piece is also 12 cm³.
Final Answer: The final answer is 12 ml or 12 cm3
Question 3.
Find the volume of a liquid present in a dish of dimensions 10 cm x 10 cm x 5 cm.
Ans:
The volume of a liquid, when contained in a dish of known dimensions, is determined by the internal volume of the container it completely fills.
Given the dimensions of the cuboid dish:
- Length (l) = 10 cm
- Breadth (b) = 10 cm
- Height (h) = 5 cm
Calculation of Volume
The geometric shape is a cuboid, and its volume (V) is calculated using the formula:
V=l×b×h
Substituting the specific values of the dish:
V=10 cm×10 cm×5 cmV=100 cm2×5 cmV=500 cm3
Therefore, the volume of the liquid that completely fills the dish is 500 cubic centimeters (cm3) .
Volume Conversion
In metric units, there is a direct equivalence between the volume in cubic measure and the capacity measure:
1 cm3=1 milliliter (ml)
Applying this conversion to the calculated volume:
V=500 cm3=500 ml
The volume of the liquid in the dish is 500 ml.
Question 4.
A rectangular field is of length 60 m and breadth 35 m. Find the area of the field.
Ans:
To find the area of a rectangular field, we use the formula:
Area = Length × Breadth
Given:
Length = 60 m
Breadth = 35 m
Substitute the values into the formula:
Area = 60 m × 35 m
Area = 2100 m²
Therefore, the area of the rectangular field is 2100 square meters.
Question 5.
Find the approximate area of an irregular lamina of which boundary line is drawn on the graph paper shown in fig. 1.16. below.
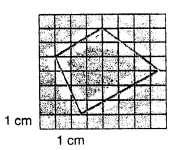
Ans:
The irregular lamina has an estimated area of approximately 16 cm². This calculation is based on the observation that there are 8 fully enclosed squares within the shape and 8 additional squares that are mostly covered—each contributing roughly 1 cm². Since each square on the graph paper represents 1 cm², the total estimated area is the sum of these, giving a total of 16 cm².
Question 6.
A piece of brass of volume 30 cm3 has a mass of 252 g. Find the density of brass in (i) g cm-3, (ii) kg m-3.
Ans:
Here is the step-by-step calculation for the density of brass, presented uniquely:
The fundamental relationship between mass, volume, and density is:
Density(ρ)=Volume(V)Mass(m)
1. Density in Grams per Cubic Centimeter (g cm−3)
We are given the following values:
- Mass of brass (m) = 252 g
- Volume of brass (V) = 30 cm3
Substituting the values into the density formula:
ρ=30 cm3252 g
ρ=8.4 g cm−3
The density of the brass is 8.4 g cm−3.
2. Density in Kilograms per Cubic Meter (kg m−3)
To express the density in the SI unit (kg m−3), we use the following conversion factors:
- 1 g=0.001 kg
- 1 cm3=(0.01 m)3=0.000001 m3
The simplest method is to use the direct conversion factor:
1 g cm−3=1000 kg m−3
Applying this factor to the calculated density:
ρ=8.4 g cm−3×(1 g cm−31000 kg m−3)
ρ=8400 kg m−3
The density of the brass is 8400 kg m−3.
Question 7.
The mass of an iron ball is 312 g. The density of iron is 7.8 g cm-3. Find the volume of the ball.
Ans:
Given:
Mass of the iron ball (m) = 312 g
Density of iron (ρ) = 7.8 g cm⁻³
We know the formula for density:
ρ = m / V
To find the volume (V), we can rearrange the formula:
V = m / ρ
Now, substitute the given values:
V = 312 g / 7.8 g cm⁻³
V = 40 cm³
Therefore, the volume of the iron ball is 40 cubic centimeters.
Final Answer: The final answer is 40 cm3
Question 8.
A cork has a volume 25 cm3. The density of cork is 0.25 g cm-3. Find the mass of cork.
Ans:
Given:
Volume of cork (V) = 25 cm³
Density of cork (ρ) = 0.25 g cm⁻³
We know the formula for density:
ρ = m / V
To find the mass (m), we can rearrange the formula:
m = ρ × V
Now, substitute the given values:
m = 0.25 g cm⁻³ × 25 cm³
m = 6.25 g
Therefore, the mass of the cork is 6.25 grams.
Final Answer: The final answer is 6.25 g
Question 9.
The mass of 5 litre of water is 5 kg. Find the density of water in g cm-3.
Ans:
Given:
Volume of water = 5
litres Mass of water = 5 kg
First, we need to convert the volume to cubic centimeters (cm³) and the mass to grams (g) to find the density in g cm⁻³.
Conversion of Volume:
We know that 1 litre = 1000 cm³
So, 5 litres = 5 × 1000 cm³ = 5000 cm³
Conversion of Mass:
We know that 1 kg = 1000 g
So, 5 kg = 5 × 1000 g = 5000 g
Now, we can calculate the density using the formula:
Density (ρ) = Mass (m) / Volume (V)
ρ = 5000 g / 5000 cm³
ρ = 1 g cm⁻³
Therefore, the density of water is 1 gram per cubic centimeter.
Final Answer: The final answer is 1 g cm−3
Question 10.
A cubical tank of side 1 m is filled with 800 kg of a liquid. Find: (i) the volume of tank, (ii) the density of liquid in kg m-3.
Ans:
Given:
The tank is cubical with a side length of 1 m.
The mass of the liquid in the tank is 800 kg.
(i) Volume of the tank:
For a cube, all sides are equal.
The volume of a cube is given by the formula: Volume = (side)³
In this case, the side of the tank is 1 m.
Volume = (1 m)³
Volume = 1 m × 1 m × 1 m
Volume = 1 m³
So, the volume of the tank is 1 cubic meter.
(ii) Density of the liquid in kg m⁻³:
The density (ρ) of a substance is given by the formula:
Density = Mass / Volume
We are given:
Mass of the liquid = 800 kg
Volume of the liquid (which is equal to the volume of the tank as it’s filled) = 1 m³
Now, we can calculate the density:
Density = 800 kg / 1 m³
Density = 800 kg m⁻³
So, the density of the liquid is 800 kilograms per cubic meter.
Final Answer: The final answer is i)1m3,ii)800kgm−3
Question 11.
A block of iron has dimensions 2 m × 0.5 m × 0.25 m. The density of iron is 7.8 g cm-3. Find the mass of block.
Ans:
The objective is to determine the mass of an iron block, given its dimensions and the density of iron. The calculation requires finding the volume first and then using the density formula, ensuring all units are consistent.
Calculation Steps
1. Determine the Volume (V)
The block is a cuboid with the following dimensions:
- Length (l) = 2 m
- Breadth (b) = 0.5 m
- Height (h) = 0.25 m
The volume is calculated as:
V=l×b×hV=2 m×0.5 m×0.25 mV=1.0 m2×0.25 m
V=0.25 m3
2. Convert Volume to Consistent Units
The density (ρ) of iron is given as 7.8 g cm−3. To use this value, the volume must be converted from cubic meters (m3) to cubic centimeters (cm3). Knowing that 1 m=100 cm, we have:
1 m3=(100 cm)3=1,000,000 cm3
Converting the volume:
Vcm3=0.25 m3×1,000,000m3cm3
V=250,000 cm3
3. Calculate the Mass (m)
The formula relating density, mass, and volume is: $$\text{Density} (\rho) = \frac{\text{Mass} (m)}{\text{Volume} (V)}$$Rearranging to solve for mass:
m=ρ×V
Substitute the values:
m=7.8cm3g×250,000 cm3
m=1,950,000 g
4. Convert Mass to Kilograms (kg)
To express the mass in the standard unit of kilograms (kg), we use the conversion factor 1 kg=1000 g:
mkg=1000kgg1,950,000 g
m=1950 kg
The mass of the iron block is 1950 kilograms.
Question 12.
The mass of a lead piece is 115 g. When it is immersed into a measuring cylinder, the water level rises from 20 ml mark to 30 ml mark.
Find:
(i) the volume of the lead piece,
(ii) the density of the lead in kg m-3.
Ans:
Given:
Mass of the lead piece (m) = 115 g
Initial water level in the measuring cylinder (V1) = 20 ml
Final water level in the measuring cylinder after immersion (V2) = 30 ml
(i) The volume of the lead piece:
The volume of the lead piece is equal to the volume of water displaced in the measuring cylinder.
Volume of lead piece = Final water level (V2) – Initial water level (V1)
Volume of lead piece = 30 ml – 20 ml
Volume of lead piece = 10 ml
Since 1 ml is equal to 1 cm³, the volume of the lead piece is also 10 cm³.
(ii) The density of the lead in kg m⁻³:
First, let’s find the density in g cm⁻³:
Density (ρ) = Mass (m) / Volume (V)
ρ = 115 g / 10 cm³
ρ = 11.5 g cm⁻³
Now, we need to convert the density from g cm⁻³ to kg m⁻³. We use the conversion factor: 1 g cm⁻³ = 1000 kg m⁻³
Density of lead in kg m⁻³ = 11.5 g cm⁻³ × 1000 kg m⁻³/g cm⁻³
Density of lead in kg m⁻³ = 11500 kg m⁻³
Final Answer: The final answer is i)10 cm3,ii)11500 kg m−3
Question 13.
The density of copper is 8.9 g cm-3. What will be its density in kg m-3 ?
Ans:
Given:
Density of copper (ρ) = 8.9 g cm⁻³
To convert the density from g cm⁻³ to kg m⁻³, we use the conversion factor: 1 g cm⁻³ = 1000 kg m⁻³
So, the density of copper in kg m⁻³ is:
ρ = 8.9 g cm⁻³ × 1000 kg m⁻³/g cm⁻³
ρ = 8900 kg m⁻³
Final Answer: The final answer is 8900 kg m−3
Question 14.
A car travels a distance of 15 km in 20 minute. Find the speed of the car in (i) km h-1, (ii) m s-1.
Ans:
To determine the car’s velocity, we use the fundamental relationship: Speed=TimeDistance. The calculation is performed using the given data: Distance (d) = 15 km and Time (t) = 20 minutes, and the result is presented in the two required units.
1. Speed in Kilometers Per Hour (km h−1)
The distance is already in kilometers (km), so we must convert the time from minutes to hours (h).
A. Convert Time to Hours
There are 60 minutes in 1 hour.
t=20 minutes=6020 hours=31 hours
B. Calculate Speed
Speed=TimeDistance=31 h15 kmSpeed=15×3 km h−1Speed=45 km h−1
2. Speed in Meters Per Second (m s−1)
To use the metric units, we must convert the distance to meters (m) and the time to seconds (s).
A. Convert Distance to Meters
d=15 km×1 km1000 m=15,000 m
B. Convert Time to Seconds
t=20 minutes×1 minute60 seconds=1,200 seconds
C. Calculate Speed
Speed=TimeDistance=1,200 s15,000 mSpeed=12150 m s−1Speed=225 m s−1
Speed=12.5 m s−1
Question 15.
How long a train will take to travel a distance of 200 km with a speed of 60 km h-1 ?
Ans:
Given:
Distance (d) = 200 km
Speed (s) = 60 km h⁻¹
We need to find the time (t) taken by the train to travel this distance.
We can use the formula: Speed = Distance / Time
Rearranging the formula to solve for time:
Time = Distance / Speed
Now, substitute the given values:
Time = 200 km / 60 km h⁻¹
Time = 200/60 hours
Time = 20/6 hours
Time = 10/3 hours
To express this time in hours and minutes:
10/3 hours = 3 and 1/3 hours
The whole number part is 3 hours.
To convert the fractional part (1/3 hour) to minutes, we multiply by 60:
(1/3) hour × 60 minutes/hour = 20 minutes
So, the train will take 3 hours and 20 minutes to travel a distance of 200 km with a speed of 60 km h⁻¹.
Final Answer: The final answer is 3 hours and 20 minutes
Question 16.
A boy travels with a speed of 10 m s-1 for 30 minute. How much distance does he travel ?
Ans:
Calculation of Distance Traveled
The following calculation determines the total distance covered by the boy using the provided speed and duration.
Given Parameters
| Variable | Value | Unit |
| Speed (s) | 10 | m/s |
| Time (t) | 30 | minutes |
Export to Sheets
Step 1: Unit Conversion (Time)
To maintain consistent units for the calculation (meters and seconds), the time must be converted from minutes to seconds:
tseconds=tminutes×1 minute60 seconds
tseconds=30 minutes×60 s/min
t=1800 seconds
Step 2: Calculate Distance in Meters
The fundamental formula relating distance, speed, and time is:
Distance (d)=Speed (s)×Time (t)
Substituting the consistent values:
d=10 m/s×1800 s
d=18000 meters
Step 3: Convert Distance to Kilometers
To express the result in the larger unit of kilometers (km), divide the meter value by 1000 (since 1 km=1000 m):
dkm=1000 m/km18000 m
d=18 km
The boy covers a total distance of 18,000 meters or 18 kilometers.
Question 17.
Express 36 km h-1 in m s-1
Ans:
To convert 36 km h⁻¹ to m s⁻¹, multiply by 3600/1000:
36×3600/1000=36×5/18=2×5=10
So, 36 km h⁻¹ = 10 m s⁻¹.
Question 18.
Express 15 m s-1 in km h-1.
Ans:
To express 15 m s⁻¹ in km h⁻¹, we need to convert meters to kilometers and seconds to hours.
We know that:
1 meter (m) = 1000/1 kilometer (km)
1 second (s) = 3600/1 hour (h)
15s/m=15×36001 h10001 km
Now, we can simplify the expression:
15×1000/1×1/3600 h/km=15×1000/3600hkm
15×10/36 h/km=15×3.6h/km
15×3.6=54
Therefore, 15 m s⁻¹ is equal to 54 km h⁻¹.
Final Answer: The final answer is 54 km h−1


