1. Force
We cannot see a force itself, but we can observe its effects.
2. Effects of Force
A force can:
Change the speed of a moving object.
Change the direction of a moving object.
Change the shape or size of an object.
3. Types of Forces
Contact Forces: Act when objects touch (e.g., muscular force, friction).
Non-Contact Forces: Act without physical contact (e.g., magnetic force, gravitational force, electrostatic force).
4. Pressure
Pressure is the force acting on a specific area.
Formula: Pressure = Force / Area
Unit: Pascal (Pa) or Newton per square meter (N/m²).
5. Pressure in Daily Life
A sharp knife cuts easily because its fine edge has a very small area, creating high pressure.
School bags have wide straps to increase the area, which reduces pressure on the shoulders.
Buildings have wide foundations to spread the force over a larger area, reducing pressure on the ground.
6. Pressure in Fluids
Pressure in liquids increases with depth.
Atmospheric Pressure is the pressure exerted by the weight of the air around us.
In short: Force is the push or pull, while pressure is the concentration of that force on an area. A smaller area results in higher pressure for the same force.
Test yourself
A. Objective Questions
1. Write true or false for each statement
(a) The S.I. unit of force is kgf.
Ans: False.
The S.I. unit of force is newton.
(b) A force always produces both the linear and turning motions.
Ans: False.
(c) Moment of force = force × perpendicular distance of force – from the pivoted point.
Ans: True.
(d) Less force is needed when applied at a farther distance from the pivoted point.
Ans:True.
(e) For a given thrust, pressure is more on a surface of large j area.
Ans:False.
For a given thrust, pressure is less on a surface of large area.
(f) The pressure on a surface increases with an increase in the thrust on the surface.
Ans: True.
(g) A man exerts same pressure on the ground whether he is standing or he is lying.
Ans: False.
A man exerts different pressure on the ground whether he is standing or he is lying.
(h) It is easier to hammer a blunt nail into a piece of wood than a sharply pointed nail.
Ans: False.
It is not easier to hammer a blunt nail into a piece of wood than a sharply pointed nail.
(i) The S.I. unit of pressure is pascal.
Ans: True.
(j) Water in a lake exerts pressure only at its bottom.
Ans: False.
(k) A liquid exerts pressure in all directions.
Ans: True.
(l) Gases exert pressure in all directions.
Ans: True.
(m) The atmospheric pressure is nearly 105 Pa.
Ans: True.
(n) Higher we go, greater is the air pressure.
Ans: False.
2. Fill in the blanks
(a) 1 kgf = 10 N (nearly).
(b) Moment of force = force × distance of force from the point of turning
(c) In a door, handle is provided farthest from the hinges.
(d) The unit of thrust is newton .
(e) Thrust is the normal force acting on a surface.
(f) Pressure is the thrust acting on a surface of unit area.
(g) The unit of pressure is pascal
(h) Pressure is reduced if area of surface increases.
(i) Pressure in a liquid increases with the depth.
(j) The atmospheric pressure on earth surface is nearly 105 Pa.
Ans:
(a) 1 kgf = 10 N (nearly).
(b) Moment of force = force × distance of force from the point of turning
(c) In a door, handle is provided farthest from the hinges.
(d) The unit of thrust is Newton .
(e) Thrust is the normal force acting on a surface.
(f) Pressure is the thrust acting on a surface of a unit area.
(g) The unit of pressure is pascal
(h) Pressure is reduced if the area of the surface increases.
(i) Pressure in a liquid increases with depth.
(j) The atmospheric pressure on the earth surface is nearly 105 Pa.
3. Match the following

4. Select the correct alternative
(a) SI. unit of moment of force ¡s
- N
- N cm
- kgfm
- N m
Ans: N m
(b) To obtain a given moment of force for turning a body, the force needed can be decreased by
- applying the force at the pivoted point
- applying the force very close to the pivoted point
- applying the force farthest from the pivoted point
- none of the above
Ans: applying the force farthest from the pivoted point
(c) The unit of thrust is
- kgf
- kg
- g
- m s-1
Ans: kgf
(d) The unit of pressure is
- N × m
- kgf
- N m-2
- kgf m2
Ans: N m-2
(e) The pressure and thrust are related as
- Pressure = Thrust
- Pressure = Thrust x Area
- Pressure = Thrust / Area,
- Pressure = Area / Thrust
Ans: Pressure = Thrust / Area,
(f) A body weighing 5 kgf, placed on a surface of area 0.1 m2, exerts a thrust on the surface equal to
- 50 kgf
- 5 kgf
- 50 kgf m-2
- 5 kgf m-2
Ans: 5 kgf
P.Q. A body weighing 5 kgf, placed on a surface of area 0.1 m2, exerts a pressure on the surface equal to
- 50 kgf
- 5 kgf
- 50 kgf m-2
- 5 kgf m-2
Ans: 50 kgf m-2
(g) The feet of lizards act like
- moving pads
- drilling pads
- suction pads
- none of the above
Ans: suction pads
(h) Pressure exerted by a liquid is due to its
- weight
- mass
- volume
- Area
Ans: weight
(i) Pressure inside a liquid increases with :
- increase in depth
- decrease in depth
- decrease in density
- none of the above
Ans: increase in depth
(j) The atmospheric pressure at sea level is nearly
- 10 Pa
- 100,000 Pa
- 100 Pa
- 10,000 Pa
Ans: 100,000 Pa
(k) Nose bleeding may occur at a high altitude because
- the atmospheric pressure decreases
- the oxygen content of atmosphere decreases
- the atmospheric pressure increasess
- there are strong air currents at the high altitude
Ans: the oxygen content of atmosphere decreases
B. Short/Long Answer Questions
Question 1. Define force. State its S.I. unit.
Ans: Force is a push or pull which changes or tends to change the state of rest or of uniform motion of a body in a straight line.The S.I. unit of force is the newton (symbol: N).
Question 2. State two effects of a force when applied on a body.
Ans:Two effects of force are:
It can change the state of motion – A football starts moving when kicked.
It can change the shape and size – Squeezing a rubber ball flattens it.
Question 3. How does the effect of force differ when it is applied on (i) a I rigid body, and (ii) a non-rigid body
Ans: When a force is applied:
(i) On a Rigid Body:It can change its state of motion (start, stop, or change speed/direction).It can make the body rotate if the force is not applied at the center of mass.The shape and size of the body do not change.
(ii) On a Non-Rigid Body:
It mainly changes the body’s shape and size (e.g., compression, stretching, or bending).A change in motion may also happen, but the key effect is the deformation of the body.
Question 4. State the effect of force F in each of the following diagram
Ans:
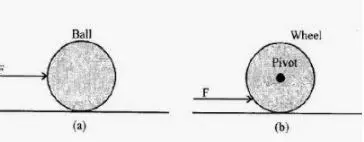
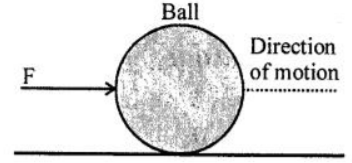
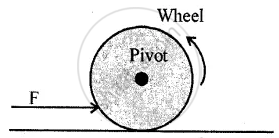
Question 5. Define the term moment of force.
Ans: Moment of force is the measure of the turning effect produced by a force about a fixed point or axis. It is calculated as the product of the force and the perpendicular distance from the pivot point to the line of action of the force.
Question 6. State the S.I. unit of moment of force.
Ans: The S.I. unit of moment of force is the newton-metre (N m).
Question 7. State two factors on which affect moment of force.
Ans: The two factors on which the moment of force depends are:
The magnitude of the applied force: A larger force produces a greater turning effect.
The perpendicular distance from the pivot: A greater distance from the pivot point results in a greater turning effect.The two factors on which the moment of force depends are:
Question 8. In Fig. a force F is applied in a direction passing through the pivoted point O of the body. Will the body rotate ? Give reason to support your answer.
Ans: No, the body will not rotate.
Reason:The applied force F passes directly through the pivot point O, so its perpendicular distance from O is zero.
Since torque (turning effect) is given by τ=F×d
where d is the perpendicular distance from pivot to the line of action of force,
here
d=0, so torque is zero.
Hence, there is no rotation.
Question 9. Write the expression for the moment of force about a given axis of rotation.
Ans: Torque measures the turning effect of a force.
It is calculated as:
Torque = Force × Perpendicular Distance
A larger force or a longer perpendicular distance creates a stronger turning effect.
Question 10. State one way to decrease the moment of a given force about a given axis of rotation.
Ans: One way to decrease the moment of a given force about a given axis of rotation is to decrease the perpendicular distance between the line of action of the force and the axis of rotation.
Explanation:The moment of a force (or torque) is calculated as the product of the force and the perpendicular distance from the axis of rotation to the line of action of the force (Moment = Force × Perpendicular Distance). Since the force is given and remains constant, reducing this perpendicular distance will directly result in a smaller turning effect or moment. For example, to loosen a nut, you apply a force at the end of a wrench. If you were to apply the same force closer to the nut (i.e., closer to the axis of rotation), it would be harder to turn because the moment would be decreased.
Question 11. State one way to obtain greater moment of a given force about a given axis of rotation.
Ans: A simple and effective way to get a greater turning effect, or moment, from a specific force is to increase the perpendicular distance between the pivot point and where the force is applied.This works because the moment of a force is not just about how hard you push or pull; it is a combination of the force’s strength and its leverage. The calculation for moment is:
Moment = Force × Perpendicular Distance
Since the force in this scenario is fixed and cannot be changed, the only variable we can adjust is the distance. By increasing this distance, we are directly multiplying the same force by a larger number, which results in a larger moment.
A common real-world example is loosening a tight bolt. If you try to turn it with a short wrench, you might struggle because the distance is small, resulting in a small turning effect. However, if you slide a long pipe over the same wrench to extend its handle, you are significantly increasing the perpendicular distance. Now, with the exact same amount of muscular force, you can produce a much greater turning moment, making it easier to loosen the bolt. This demonstrates how crucial the distance is in achieving a greater rotational effect with a constant force.
Question 12. What do you mean by the clockwise and anti-clockwise moment of force ?
Ans: Clockwise Moment:
A force causing rotation in the same direction as a clock’s hands.
Anti-clockwise Moment:
A force causing rotation opposite to a clock’s hands.
These opposing moments are used to find the net torque and check if an object is in rotational balance.
Question 13. Explain the following: (a) The spanner (or wrench) has a long handle. (b) The steering wheel of a vehicle is of large diameter. (c) The hand flour grinder is provided with a handle near the rim. (d) It is easier to open the door by pushing it at its free end. (e) A potter turns his wheel by applying a force through the stick near the rim of wheel.
Ans: (a) The spanner has a long handle.
A long handle increases the perpendicular distance between the pivot point (the nut) and the point of force application. This increases the turning effect (torque), making it easier to loosen or tighten the nut with less effort.
(b) The steering wheel of a vehicle is of large diameter.
A large diameter wheel increases the leverage. This allows the driver to turn the steering wheel and rotate the axle with a much smaller force, making steering easier.
(c) The hand flour grinder is provided with a handle near the rim.
Placing the handle near the rim maximizes the distance from the central pivot. This increases the torque for a given applied force, making it easier to rotate the heavy grinding stone.
(d) It is easier to open the door by pushing it at its free end.
Pushing at the free end, which is farthest from the hinges (the pivot), provides the greatest possible distance for force application. This maximizes the torque, making the door turn more easily.
(e) A potter turns his wheel by applying a force through the stick near the rim of the wheel.
By applying the force near the rim, the potter maximizes the distance from the central axle. This generates a higher torque with the same amount of force, allowing the heavy wheel to be spun easily and maintained at a constant speed.
Question 14. What is thrust ?
Ans:Thrust is a mechanical force that pushes an object like a plane or rocket forward. It is created when an engine expels mass, such as hot exhaust gases, backward. This action produces an equal and opposite reaction, propelling the vehicle forward, as described by Newton’s Third Law of Motion.
Question 15. State the unit of thrust .
Ans: The unit of thrust is the newton (N).
Question 16. On what factors does the effect of thrust on a surface depend?
Ans: The effect of thrust on a surface depends on:
The magnitude of the thrust (force): A larger force has a greater effect.
The area of the surface on which it acts: The same force applied over a smaller area has a greater effect.
In short, the effect of thrust depends on the force and the area over which it applied. This is why the concept of pressure (force/area) is used.
Question 17. Define the term ‘pressure’ and state its unit.
Ans: Pressure is the perpendicular force applied per unit area.
Its SI unit is the pascal (Pa).
One pascal equals one newton of force acting on one square metre of area (1 Pa = 1 N/m²).
Question 18. How is the thrust related to pressure ?
Ans: Thrust is directly related to pressure.
Pressure is the force acting per unit area.
The relationship is given by:
Thrust = Pressure × Area
or
Pressure = Thrust / Area
In simple terms, thrust is the product of pressure and the area over which it acts. A higher pressure on a given area will result in a greater thrust.
Question 19. Name two factors on which the pressure on a surface depends.
Ans: The pressure on a surface depends on:
Force Applied: The amount of push acting perpendicularly on the surface. More force results in more pressure.
Area of Contact: The size of the surface on which the force is distributed. A smaller area results in greater pressure.
Question 20. When does a man exert more pressure on the floor : while standing or while walking ?
Ans: While walking, a man exerts more pressure on the floor than while standing.
This is because pressure = force / area.
While standing, the force (his weight) is distributed over the total area of both his feet.
While walking, his weight is supported by only one foot at a time. Since the area is halved (one foot instead of two), the pressure on the floor doubles for that moment.
Question 21. Why do camels or elephants have broad feet ?
Ans: Camels and elephants have broad feet primarily to cope with their immense body weight and the soft, unstable ground they often walk on. The broadness of their feet plays a crucial role through a scientific principle called pressure.
Pressure is defined as force per unit area (Pressure = Force / Area).
An elephant or a camel exerts a very large force (its weight) downwards due to gravity. If this enormous force were applied through small, narrow feet (a small area), the pressure on the ground would be extremely high. This would cause their feet to sink deeply into soft surfaces like desert sand or muddy forest floors, making it very difficult and energy-consuming to walk.By having broad feet, they significantly increase the surface area in contact with the ground. When the same force (their weight) is spread over a larger area, the pressure exerted on the ground is greatly reduced.This is similar to how a person wearing snowshoes can walk on snow without sinking, while someone in regular boots will sink in. The snowshoe spreads the person’s weight over a larger area, reducing the pressure.
Question 22. A sharp pin works better than a blunt pin. Explain the reason.
Ans: A sharp pin exerts pressure on a very small area, creating a very high pressure. A blunt pin has a larger area, so the same force produces much less pressure. This high pressure from a sharp pin allows it to pierce materials easily.
Question 23. Why is the bottom part of the foundation of a building made wider ?
Ans: The bottom part of a building’s foundation, known as the footing, is made wider for a crucial engineering reason: to distribute the immense load of the entire structure over a larger area of soil.This fundamental principle can be understood by thinking about the relationship between pressure, force, and area.
1. The Science of Pressure Distribution:
Imagine two people walking on soft ground. One is wearing high-heeled shoes, and the other is wearing flat, wide snowshoes. The person in high heels will sink into the ground because the entire weight of their body is concentrated on the very small area of the heel. The person wearing snowshoes, however, will walk easily because their weight is spread out over a much larger area.
A building works in the exact same way. The total weight of the building—including walls, floors, furniture, and people—is a massive force pushing down. If this force were applied to the ground through a narrow strip (like a high heel), it would create an extremely high pressure on the soil.
The formula for pressure is:
Pressure = Force / Area
By making the bottom of the foundation wider, we significantly increase the area in contact with the ground. According to the formula, for the same force (the building’s weight), increasing the area results in a decrease in the pressure exerted on the soil.
2. Ensuring Stability and Preventing Failure:
Every type of soil has a specific bearing capacity—the maximum pressure it can withstand without sinking or failing. If the pressure from the building exceeds this bearing capacity, the soil will compress unevenly, leading to dangerous consequences like:
Settlement: The building sinks into the ground.
Differential Settlement: One part of the building sinks more than another, causing cracks in walls, tilting, and in extreme cases, structural collapse.
The wider footing ensures that the pressure transferred to the soil is well within its safe bearing capacity. It acts as a stable, broad base that evenly spreads the load, preventing the building from sinking and ensuring its long-term stability and safety.
Question 24. It is easier to cut with a sharp knife than with a blunt one. Explain.
Ans: A sharp knife’s thin edge focuses force onto a tiny area, creating very high pressure for easy cutting.
A blunt knife’s thicker edge spreads the same force over a larger area, resulting in lower pressure. This makes cutting difficult, requiring more force to achieve the same result.
Question 25. A gum bottle rests on its base. If it is placed upside down, how does the (i) thrust, (ii) pressure change ?
Ans: (i) Thrust:The thrust remains the same because the weight of the gum bottle (thrust due to gravity) does not change when it is turned upside down.
(ii) Pressure:The pressure increases when the bottle is placed upside down because the same thrust (weight) acts on a smaller base area, and pressure is thrust per unit area.
Question 26. Explain the following: (a) Sleepers are used below the rails. (b) A tall building has wide foundations.
Ans: (a) Sleepers are used below the rails.
Sleepers, also called railroad ties, are used below the rails for two main reasons:
To distribute the load: A train is extremely heavy. The sleepers spread the immense pressure from the rails over a larger area of the underlying ground. This prevents the rails from sinking into the ground under the weight.
To hold the rails in place: The sleepers maintain a fixed, parallel distance (gauge) between the two rails. This ensures the train’s wheels run smoothly and safely along the track.
(b) A tall building has wide foundations.
A tall building has wide foundations to increase the area of contact between the building and the ground.The total weight (force) of the building is very high.
Pressure is force divided by area (P = F/A).
By increasing the area (A) with wide foundations, the pressure (P) exerted on the ground is significantly reduced.
This prevents the building from sinking into the soil by ensuring the pressure on the ground does not exceed its safe bearing capacity.
Question 27. Describe an experiment to show that a liquid exerts pressure at the bottom of the container in which it is kept.
Ans: Aim:To show that a liquid exerts pressure at the bottom of its container.
Apparatus:Tall glass tube (open at both ends), cork, beaker, water.
Procedure:Seal the bottom of the tube with a tight-fitting cork.
Fill the tube with water.
Observation:The cork does not fall out.
Explanation:The cork remains in place because the upward force from the container’s base balances the downward pressure exerted by the water column above it.
Conclusion:Water (a liquid) exerts pressure at the bottom of the container.
Question 28. Describe a suitable experiment to demonstrate that a liquid exerts pressure sideways also ?
Ans: Aim:
To demonstrate that a liquid exerts pressure sideways.
Materials required:
A tin can with a tight-fitting lid.
A hammer and nail.
Water.
Procedure:
Make 3–4 holes on the side wall of the tin can at different heights using the nail and hammer.
Close the lid of the can and fill it completely with water.
Observe the water coming out through the holes.
Observation:
Water flows out sideways from each hole in the form of jets. The jets are perpendicular to the side wall of the can.
Conclusion:
Since water is ejected sideways through the holes, it proves that liquids exert pressure not only downwards but also sideways.
Question 29. Describe a simple experiment to show that at a given depth, a liquid exerts same pressure in all directions.
Ans: Aim: To show that at the same depth, a liquid exerts equal pressure in all directions.
Apparatus: A thin-walled, flexible rubber tube with a funnel at one end. The mouth of the funnel is closed by a rubber membrane. Water.
Procedure:
Fill the rubber tube and funnel with water.
Place the funnel at a fixed depth inside a beaker full of water.
Now, orient the funnel in different directions at that same depth—facing upwards, downwards, and sideways.
Observation:
It is observed that the rubber membrane bulges out by the same amount in every case, regardless of the funnel’s direction.
Conclusion:
The constant and equal bulging of the membrane shows that the pressure applied by the water at that specific depth is the same in all directions (downwards, upwards, and sideways).
Question 30. State two factors on which the pressure at a point in a liquid depends.
Ans: The pressure you feel at any specific point submerged in a liquid, like water at the bottom of a swimming pool or mercury in a barometer, is primarily determined by two key factors:
1. The Depth of the Point
Imagine you are swimming in a pool. When you are just below the surface, you feel a slight pressure on your eardrums. Now, if you dive down to the deep end, that pressure becomes much more intense, even painful. This is because the deeper you go, the greater the weight of the liquid column that is pushing down on you from above. It’s like having a taller stack of books pressing down; the books at the very bottom bear the most weight. In a liquid, this “weight” is the force exerted by all the liquid above that point, and it increases linearly with depth. So, pressure is directly proportional to how far the point is from the free surface.
2. The Density of the Liquid
Now, imagine two pools side-by-side: one filled with water and the other filled with thick, heavy molasses. If you were to dive to the same depth in both, you would feel a significantly greater pressure in the molasses pool. Why? Because molasses is denser than water. A denser liquid has more mass, and therefore more weight, in the same-sized column above you. This heavier column of liquid pushes down with a greater force. Therefore, for the same depth, a denser liquid will always exert a higher pressure than a less dense one.
Question 31. Describe an experiment to show that the liquid pressure at a point increases with the increase in height of the liquid column above that point.
Ans: Aim of the Experiment
To demonstrate that the liquid pressure at a point increases with the increase in the height (or depth) of the liquid column above that point.
Apparatus Required
A tall, transparent beaker or a long glass tube.
Water.
A thistle funnel with a stretched rubber membrane (like a balloon) tied tightly over its wide mouth.
A narrow, long rubber tube.
A glass tube of fine bore.
A ruler or measuring scale.
A stand with a clamp.
Procedure
Setup: Take the thistle funnel and stretch a piece of rubber membrane tightly over its wide opening, ensuring it is sealed properly. Connect the stem of the thistle funnel to one end of the long rubber tube. Connect the other end of the rubber tube to the fine glass tube.
Initial Observation: Hold the thistle funnel upright and pour some water into the glass tube. You will notice that the rubber membrane bulges out slightly. Blow gently into the open end of the glass tube. You will see the rubber membrane bulging out more. This shows that the air pressure you applied is transmitted through the water and pushes the membrane outward.
The Experiment:
Clamp the glass tube vertically to the stand. Place the ruler vertically next to it to measure the height of the water column.
Now, hold the thistle funnel such that its rubber membrane is facing upwards. Immerse it into the tall beaker filled with water. Ensure the funnel is held at a fixed depth.
Observe the water level in the glass tube. Note this initial height of the water column, h₁.
Now, slowly lower the thistle funnel deeper into the water. As you do this, you willsee that the water level in the vertical glass tube rises.
Note the new height, h₂, of the water column in the glass tube when the funnel is at a greater depth. You will find that h₂ is greater than h₁.
Observation
When the thistle funnel is lowered to a greater depth in the water, the height of the water column in the vertical glass tube increases. This indicates that the pressure acting on the rubber membrane has increased.
Explanation and Conclusion
The rubber membrane acts as a pressure sensor. When it is pushed inward by the external water pressure, it compresses the air trapped in the apparatus. This compression forces the water level in the vertical glass tube to rise. The height of this water column (h) is a direct measure of the pressure applied to the membrane.
As we increase the depth of the funnel, the height of the water column above the membrane increases. The rise in the water level in the glass tube for greater depths shows that the pressure is higher. This happens because the pressure at a point in a liquid is due to the weight of the liquid column above it. A taller column of liquid means more weight and hence, greater pressure.
Therefore, this experiment clearly verifies that the liquid pressure at a point increases with the increase in the height (or depth) of the liquid column above it.
Question 32. Which fact about liquid pressure does the diagram in fig. illustrate.
Ans: The diagram illustrates that liquid pressure increases with depth.
Question 33. Describe an experiment to show that liquid pressure depends on the density of liquid.
Ans: Apparatus Required:
A U-tube, water, salty water (or any denser liquid), and a rubber membrane or piston to separate the two liquids initially.
Procedure:
Set up a U-tube and pour water into one arm.
In the other arm, pour salty water (which has higher density than plain water) to the same initial height.
Observe the liquid levels in both arms.
Observation:
The level of salty water will be lower than that of plain water when pressure equilibrium is reached at the bottom.
Conclusion:
Since pressure at the bottom is given by
P=hρg, for the same pressure, a denser liquid (ρ larger) has a smaller height (h smaller). This shows that liquid pressure depends on the density of the liquid.
Question 34. A dam has broader walls at the bottom than at the top. Give a reason.
Ans: A dam has thicker walls at the bottom because the pressure exerted by water increases with depth.The deeper the water, the greater the pressure pushing against the dam wall. A thicker, broader base is needed to withstand this immense pressure and ensure the structure’s stability.
Question 35. What do you mean by atmospheric pressure ?
Ans: Atmospheric pressure is the force created by the weight of air in the atmosphere pressing down on the Earth’s surface. Because air has mass, gravity pulls it downward, which generates this pressure.
Question 36. Write the numerical value of the atmospheric pressure on the earth surface in pascal.
Ans: Approximately 101,325 pascals (Pa).
Question 37. We do not feel uneasy even under the enormous atmospheric pressure. Give a reason.
Ans: We do not feel atmospheric pressure because the pressure inside our bodies pushes outward with a force equal to the air pressure pushing inward. These balanced opposing forces cancel each other out, so we feel no discomfort.
Question 38. Describe a simple experiment to illustrate that air exerts pressure.
Ans: Aim: To show that air exerts pressure.
Materials needed: A glass of water and a stiff cardboard piece.
Procedure:
Fill the glass completely with water.
Place the stiff cardboard piece over the mouth of the glass, covering it completely.
Pressing the cardboard gently with your hand, quickly invert the glass.
Now, carefully remove your hand from the cardboard.
Observation: The cardboard does not fall down and the water remains in the glass.
Explanation: The air pressure acting upwards on the cardboard is greater than the pressure of the water inside the glass acting downwards. This higher external atmospheric pressure holds the cardboard in place, proving that air exerts pressure.
Question 39. bescribe the crushing tin can experiment. What do you conclude from this experiment ?
Ans: Experiment:
Take an empty tin can with a tight-fitting lid.
Add a small amount of water to it and heat it until the water boils and steam pushes the air out.
After a few minutes, securely close the lid and immediately cool the can rapidly by pouring cold water over it or immersing it in cold water.
Observation:
The can crushes inwards instantly and violently, as if squeezed by a giant hand.
Conclusion:
This experiment concludes that the pressure exerted by the atmosphere (atmospheric pressure) is very strong. When the steam inside condenses back into water, it creates a vacuum and a very low pressure inside the can. The outside atmospheric pressure, now being much greater, crushes the can. This proves that air exerts a large amount of pressure in all directions.
Question 40. Give reasons for the following : (a) A balloon collapses when air is removed from it. (b) Water does not run out of a dropper unless its rubber bulb is pressed. (c) Two holes are made in a sealed oil tin to take out oil from it.
Ans: (a) A balloon collapses when air is removed from it.
The air inside the balloon exerts pressure on its walls, keeping it inflated. When air is removed, the outside atmospheric pressure becomes greater than the pressure inside. This higher outside pressure crushes the balloon.
(b) Water does not run out of a dropper unless its rubber bulb is pressed.
Releasing the bulb reduces pressure inside, so atmospheric pressure pushes the liquid up into the dropper. To release the liquid, pressing the bulb increases pressure inside, forcing the water out.
(c) Two holes are made in a sealed oil tin to take out oil from it.
With only one hole, air cannot enter the tin as oil flows out, which creates a partial vacuum inside and stops the oil flow. A second hole lets air enter, maintaining atmospheric pressure inside and allowing smooth oil flow.
Question 41. How does the atmospheric pressure change with altitude?
Ans: Atmospheric pressure decreases with altitude.
This happens because air has weight, and the pressure is caused by the weight of the air above you. As you go higher, there is less air above you pushing down, so the weight and the pressure decrease.
The decrease is rapid at first near the ground and becomes more gradual at higher altitudes.
C. Numericals
Question 1. Find the moment of force of 20 N about an axis of rotation at distance 0.5 m from the force.
Ans: The moment of force (torque) is given by:
τ = F × d
where F = 20 N ,
d = 0.5 m .
τ = 20 × 0.5 = 10 Nm
τ=20×0.5=10 Nm
Moment of force = 10 Nm
Question 2. The moment of a force of 25 N about a point is 2.5 N m. Find the perpendicular distance of force from that point
Ans: Step 1: Recall the formula for the moment of a force
The moment M of a force
F about a point is given by:M=F×d
where:
M = moment in newton-meters (N m),
F = magnitude of force in newtons (N),
d = perpendicular distance from the point to the line of action of the force in meters (m).
Step 2: We are given:
M=2.5 N m,F=25 N
2.5=25×d
Step 3: Solve for
d=2.5 =0.1 m
Step 4: Final answer0.1
The perpendicular distance of the force from the point is 0.1 meter.
Question 3. A spanner of length 10 cm is used to open a nut by applying a minimum force of 5.0 N. Calculate the moment of force required.
Ans: Step 1: Understanding the problem
A spanner is used to turn a nut, so the force applied produces a turning effect called the moment of force (or torque).
We are given:
Length of spanner = 10 cm = 0.10 m
Minimum force required = 5.0 N
The force is applied at the end of the spanner perpendicularly to get the minimum force (so that sin θ = 1).
Step 2: Formula for moment of force
Moment of force = Force × perpendicular distance from pivot
M=F×d
Here,
F=5.0 N
d=0.10 m
Step 3: Calculation
M=5.0×0.10
M=0.50 Nm
Step 4: Final answer0.50 Nm
The moment of force required is 0.50 newton-metre.
Question 4. A wheel of diameter 2 in can be rotated about an axis passing through its centre by a moment of force equal to 2e0 N m. What minimum force must be applied on its rim?
Ans: Step 1: Interpret the problem
We have:
Diameter of wheel
d=2 in
Moment of force (torque) needed:
τ=2N m (I assume “2e0” means 2×100=2)
We want the minimum force applied at the rim to produce this torque.
Step 2: Relate torque and force
The torque is given by:
τ=F×r
where r is the radius of the wheel.
Diameter d=2 in
So radius
r=d2=1 in
Step 3: Convert radius to meters
We know
1 in=0.0254 m.
r=1 in=0.0254 m
Step 4: Solve for force
F=τr
=2 N m
0.0254 m
F≈78.74 N
Step 5: Conclusion
The minimum force applied tangentially at the rim is:78.74(Units: Newtons)
Question 5. A normal force of 200 N acts on an area of 0.02 m2. Find the pressure in pascal.
Ans: Normal force, F = 200
Area, A = 0.02 m 2
Formula: Pressure = Force Area
Calculation: P = 200 0.02 = 10000
Pa/P= 0.02 /200 =10000Pa
Answer: 10000
Question 6. Find the thrust required to exert a pressure of 50000 pascals on an area of 0.05 m2 ?
Ans: We are given:
Pressure (P) = 50,000 Pascals
Area (A) = 0.05 m²
We need to find the Thrust (F)
We know the fundamental formula for pressure:
Pressure = Thrust / Area
or
P=F/A
To find the thrust (F), we rearrange this formula:
F=P×A
Now, we substitute the given values into this equation:
F=50,000 Pa×0.05 m 2
Let’s perform the multiplication:
F=50,000×0.05
F=2,500
Since the units are Pascals (N/m²) and square meters (m²), the resulting unit for force is Newtons (N).
Therefore, the thrust required is 2,500 Newtons.
Question 7. Find the area of a body which experiences a pressure of50000 Pa by a thrust of 100 N ?
Ans: Given:
Pressure P = 50000 Pa
Thrust F = 100 N
Formula: P = F /A
Calculation: A = 100 /50000 = 0.002 m 2
Final Answer: 0.002 m 2
Question 8. of 30 cm2 Calculate the pressure in pascal exerted by a force of 300 N acting normally on an area .
Ans: Step 1: Understanding the Problem
We are given:
Force (F) = 300 N (Newton)
Area (A) = 30 cm² (square centimetres)
The force is acting normally on the area, which means it is acting perpendicularly. This is the standard condition for calculating pressure.
We need to find the Pressure (P) in pascals (Pa).
Step 2: Recalling the Formula
The fundamental formula for pressure is:
Pressure (P) = Force (F) / Area (A)
or
P = F / A
Step 3: Unit Conversion
The units given are not directly compatible with the pascal unit.
Force is in Newton (N), which is correct.
Area is in cm², but the SI unit for area is m² (square metre).
By definition, 1 Pascal = 1 Newton per square metre (1 Pa = 1 N/m²).
Therefore, we must convert the area from cm² to m².
We know that:
1 m = 100 cm
Squaring both sides:
1 m² = (100 cm)² = 10,000 cm²
So,
30 cm² = 30 / 10,000 m²
30 cm² = 0.003 m²
Step 4: Calculation
Now we substitute the values into the formula:
P = F / A
P = 300 N / 0.003 m²
P = 100,000 N/m²
Since 1 N/m² = 1 Pa,
P = 100,000 Pa
This can also be written as 1 × 10⁵ Pa.
Final Answer:The pressure exerted is 100,000 Pascals or 1 × 10⁵ Pa.
Question 9. How much thrust will be required to exert a pressure of 20,000 Pa on an area of 1 cm2.
Ans: We are given:
Pressure (P) = 20,000 Pascals (Pa)
Area (A) = 1 cm²
We need to find:
Thrust (Force, F)
Step 1:The formula for pressure is:
Pressure (P)=Force (F)/Area (A)
We can rearrange this formula to solve for Force (which is the same as Thrust in this context):
Force (F)=Pressure (P)×Area (A)
Step 2: Convert the area to the correct unit
The standard unit for area in the SI system is the square meter (m²). Our pressure is given in Pascals (Pa), and 1 Pascal is defined as 1 Newton per square meter (N/m²). Therefore, we must convert the area from cm² to m².
We know that:
1 cm = 0.01 m
So,
1 cm² = (0.01 m) × (0.01 m) = 0.0001 m²
Therefore,
Area (A) = 1 cm² = 0.0001 m²
Step 3: Substitute the values into the formula
F=P×A
F=20,000Pa×0.0001m 2
Step 4: Calculate the thrust
F=20,000×0.0001N
F=2N
Final Answer:
The thrust required is 2 Newtons.
Question 10. The base of a container measures 15 cm × 20 cm. It is placed on a table top. If the weight of the container is 60 N, what is the pressure exerted by the container on the table top ?
Ans: Step 1: Understand the problem
We are given:
Base dimensions: 15cm×20cm
Weight of container: 60N
We need to find pressure exerted on the table top.
Step 2: Recall the formula for pressure
Here, the force is the weight of the container, which acts vertically downward on the table.
Step 3: Calculate the area of the base in m2
15cm=0.15m
20cm=0.20m
Area=0.15×0.20=0.03m 2
Step 4: Apply the pressure formula
P=60/0.03=2000N/m2
2=1Pa
SoP=2000Pa
Step 5: Final answer
2000Pa
Question 11. Calculate the pressure exerted on a surface of 0.5 m2 by a thrust of 100 kgf.
Ans: The pressure is calculated using the formula:
Pressure = Thrust Area
Given: Thrust = 100 kgf
Area = 0.5 m²
Pressure = 100 0.5 = 200 kgf/m 2
Final Answer: 200 kgf/m 2
Question 12. A boy weighing 60 kgf stands oixplatform of dimensions 2.5 cm x 0.5 cm. What pressure in pascal does he exert ?
Ans: Step 1: Understand the given data
Weight of the boy = 60 kgf
In SI units,
1 kgf=9.8 N
So, 60 kgf=60×9.8=588 N
Platform dimensions: 2.5 cm×0.5 cm
Step 2: Calculate the area in m²
A=length×breadth
A=2.5 cm×0.5 cm
A=1.25 cm 2
A=1.25×10 −4 m 2
Step 3: Calculate pressure
Pressure P=Force/Area
P=588/1.25×10−4
P=588/0.000125
First, = 588×1/1.25×10−4
So,0.8×10 *4=8000
Thus,
P=588×8000
P=4,704,000 Pa
Step 4: Final answer in appropriate form4704000 Pa
This is the pressure exerted by the boy on the platform in pascals.
Question 13. Figure shows a brick of weight 2 kgf and dimensions 20 cm x 10 cm × 5 cm placed in three different positions on the ground. Find the pressure exerted by the brick in each case.
Ans: Step 1: Understand the Concepts
Weight (Force): The weight of the brick is given as 2 kgf. In the SI system, we often use Newtons (N) for force. Since 1 kgf ≈ 10 N, the weight of the brick is:
2kgf×10N/kgf=20N
This is the force (F) the brick exerts on the ground in all cases.
Pressure: Pressure (P) is defined as Force (F) per unit Area (A).
P=F/A
The pressure depends on the area of contact between the brick and the ground.
Step 2: Calculate the Areas for Each Position
The brick has dimensions:
Length (L) = 20 cm = 0.2 m
Breadth (B) = 10 cm = 0.1 m
Height (H) = 5 cm = 0.05 m
We will calculate the area of the face in contact with the ground for each case. (Converting to meters ensures our pressure will be in Pascals, Pa, which is N/m²).
Case (a): The brick is resting on its largest face.
Contact Area,
A =L×B=0.2m×0.1m=0.02m 2
Case (b): The brick is resting on its side.
Contact Area,
A =L×H=0.2m×0.05m=0.01m 2
Case (c): The brick is resting on its smallest face (on its end).
Contact Area,
A =B×H=0.1m×0.05m=0.005m 2
Step 3: Calculate the Pressure for Each Case
Using the formula
P=F/A
with
F=20N.
Pressure in Case (a):
Pa=20N/0.02
=1000Pa
Pressure in Case (b):
Pb=20N/0.01m2
=2000Pa
Pressure in Case (c):
Pc=20N/0.005m2=4000Pa
Final Answer
The pressures exerted by the brick in the three different positions are:
Case (a): 1000 Pascals
Case (b): 2000 Pascals
Case (c): 4000 Pascals