Measurements and Experimentation

The Measurements and Experimentation is foundational, establishing the critical role of measurement in science. It begins by defining a physical quantity as the product of a numerical value and a unit. This leads to the distinction between fundamental units (like those for length, mass, and time, which are independent) and derived units (like speed or density, which are combinations of fundamental units). The chapter emphasizes the importance of the internationally accepted S.I. System (Système International d’Unités) as the standard for scientific communication, contrasting it with older systems like CGS and FPS. Furthermore, it details the necessary characteristics of a good unit, ensuring it is invariable, reproducible, and unambiguous.

A major focus of the chapter is the practical aspect of measuring length and achieving high accuracy. It introduces the concept of Least Count (LC)—the smallest value an instrument can measure. While a metre scale is used for basic measurements, the chapter delves into precision instruments: the Vernier Callipers and the Screw Gauge. Students learn the principles of these instruments, how to calculate their respective least counts, and the essential procedure for dealing with zero error (positive and negative). A correct reading must always compensate for this error. Beyond length, the chapter also addresses the measurement of time, introducing the Simple Pendulum as an experimental setup to accurately determine the Time Period of oscillation.

In essence, this chapter equips students with the skills to conduct accurate experiments. It covers the theoretical framework of units and systems, the practical methods for precise measurements using specialised instruments, and the techniques for correcting experimental errors. This understanding of measurement, accuracy, and precision is vital, as it forms the basis for all subsequent experimental work in physics.

Exercise 1 (A)

Question 1.

What is meant by measurement?

Ans: 

Measurement is the fundamental action in science where you determine the size or magnitude of a physical property (like length, mass, or time). This is done by a process of comparison: the quantity being measured (the unknown) is compared against a fixed, universally accepted reference of the same nature, which we call a unit.

The outcome of this comparison is a complete physical quantity, expressed as a product: a numerical value that indicates how many times the standard unit is contained within the quantity, multiplied by the unit itself. For instance, stating an object has a mass of 5 kilograms quantifies that mass as five times the defined standard kilogram unit. This systematic quantification provides the necessary objective data for all scientific analysis and experimentation.

Question 2.

What do you understand about the Term Unit?

Ans: 

A unit is a definite magnitude of a physical quantity, such as length or mass, that is fixed by convention or law and used as a standard of comparison for all other quantities of the same type.

In simple terms, a unit is the reference point that gives meaning to a numerical value in a measurement.

Measurement=Numerical Value×Unit

For example, if a rope is 10 meters long, the unit is the meter (m), which is the universally accepted standard for measuring length. The number 10 indicates that the rope is 10 times the length of the standard unit.

Essential Characteristics of a Standard Unit

For a unit to be useful in science and everyday life, it must possess several key characteristics, which are now largely embodied by the International System of Units (SI):

1. Universally Accepted (Invariable): It must be the same everywhere in the world and accepted by the international community.
2. Well-Defined: It must be defined precisely, ideally in terms of a fundamental physical constant, so that its value does not change.
3. Reproducible: It must be possible to accurately reproduce the standard in any laboratory.
4. Incorruptible: Its value should not change with time or with changes in physical conditions like temperature or pressure.
5. Appropriate Size: It should be a suitable size for measuring the quantity in question (e.g., using a meter for a desk instead of a kilometer).

Importance of Units

Units are absolutely necessary because a numerical value alone is meaningless without a reference scale.

• Clarity and Meaning: They provide context. Saying a trip took “2” is meaningless; saying it took “2 hours” is clear.
• Consistency: They ensure that measurements are the same regardless of who performs the measurement or where it is done. This allows scientists and engineers worldwide to share, compare, and reproduce data reliably (the core of the scientific method).
• Dimensional Analysis: In calculations, units are manipulated algebraically to verify that the final answer has the correct physical meaning (e.g., velocity must have units of length divided by time, like m/s).

Question 3.

What are the three requirements for selecting a unit of a physical quantity?

Ans: 

The three primary requirements for selecting a reliable and universally accepted unit of a physical quantity are Invariance, Unambiguous Definition, and Reproducibility.

These characteristics ensure the unit serves as a consistent standard for scientific and commercial use worldwide.

1. Invariance (Stability and Universality)

The value of the unit must not change with respect to changes in physical conditions, location, or time.

• Stability: The unit should remain constant over a long period. For example, the definition of the second (the SI unit of time) is now based on a specific, unchanging transition of the cesium-133 atom, making it inherently stable.
• Universality (or Invariance with Space): The unit must remain the same regardless of where the measurement is performed (on Earth, in space, or in different labs). This ensures measurements are comparable everywhere.

2. Unambiguous Definition (Clarity)

The unit must be clearly and precisely defined so that everyone can have the exact same understanding of what it represents.

• The definition should be precise enough that it can be measured with extreme accuracy.
• Ideally, the unit should be defined in terms of fundamental physical constants of nature (like the speed of light or the Planck constant), rather than a physical artifact that can be damaged or lost.

3. Reproducibility (Practicality)

It must be possible to reproduce the unit easily and accurately in any standard laboratory, allowing for consistent measurement and calibration.

• This means that the standard quantity can be easily accessed or the procedure for generating the unit can be repeated to verify the measurement.
• A unit should also be of a convenient size for practical measurements (e.g., the kilometer is used for road distances, while the millimeter is used for mechanical drawings).

Question 4.

Name the three fundamental quantities.

Ans: 

The three most commonly referenced fundamental quantities in the field of physics, particularly in classical mechanics, are:

1. Length (Unit: meter, m)
2. Mass (Unit: kilogram, kg)
3. Time (Unit: second, s)

These three quantities are considered the basic building blocks from which all other mechanical quantities (like velocity, force, and energy) can be mathematically derived.

Question 5.

Name the three systems of units and state the various fundamentals units in them.

Ans: 

System of Units	Fundamental Quantity	Unit Name	Unit Symbol
CGS System	Centimeter	Centimeter	cm
	Gram	Gram	g
	Second	Second	s
\hline
MKS System	Meter	Meter	m
	Kilogram	Kilogram	kg
	Second	Second	s
\hline
FPS System	Foot	Foot	ft
	Pound	Pound (for mass)	lb
	Second	Second	s

Question 6.

Define a fundamental unit.

Ans:

A fundamental unit (or base unit) is a standard unit of measurement for a basic physical quantity that is:

1. Independent: It is defined on its own and does not rely on any other units for its definition.
2. Basic: It cannot be broken down into simpler units.
3. Foundation: All other units of measure (derived units) are created by algebraically combining these fundamental units.

In the globally accepted International System of Units (SI), there are seven fundamental units that form the basis for all scientific measurements.

The Seven SI Fundamental Units

Base Quantity	Fundamental Unit	Symbol
Length	Meter	m
Mass	Kilogram	kg
Time	Second	s
Electric Current	Ampere	A
Thermodynamic Temperature	Kelvin	K
Amount of Substance	Mole	mol
Luminous Intensity	Candela	cd

Key Characteristics

• Non-Derivable: You cannot express a fundamental unit (like the meter) as a combination of other fundamental units (like the second and kilogram).
• Universal Definition: Their definitions are based on invariant physical constants or phenomena (e.g., the speed of light) to ensure they are the same everywhere.
• Building Blocks: Units for complex quantities like velocity (meter/second) or force (Newton, which is kg⋅m/s2) are derived from these fundamental units.

Question 7.

What are the fundamental units in the S.I system? Name them along with their symbols.

Ans: 

The fundamental units of measurement in the International System of Units (SI) are the seven Base Units. These units are independent of each other and form the foundation from which all other SI units (derived units) are created.

7 Fundamental SI Units (Base Units)

Base Quantity	SI Unit (Name)	SI Unit (Symbol)
Length	metre (or meter)	m
Mass	kilogram	kg
Time	second	s
Electric Current	ampere	A
Thermodynamic Temperature	kelvin	K
Amount of Substance	mole	mol
Luminous Intensity	candela	cd

What are Fundamental Units?

Fundamental (or Base) Units are the set of seven basic units that are not defined in terms of any other units. They are the essential building blocks for measuring physical quantities. For example, the unit for force, the Newton (N), is a derived unit because it is defined using three fundamental units: N=kg⋅m/s2.

Question 8.

Explain the meaning of the derived unit with the help of one example?

Ans: 

A derived unit is a unit of measurement created by mathematically combining two or more fundamental (base) units. These units are used to quantify physical quantities whose definitions rely on formulas involving the base quantities. While fundamental units (such as the meter, kilogram, or second) stand on their own, derived units are built upon them using multiplication, division, or exponents.

For instance, consider the unit for Speed. Speed is defined by the formula Distance/Time. By replacing these quantities with their respective fundamental SI units, we derive the unit for speed:

Unit of Speed=Unit of Time /Unit of Distance​=second (s)meter (m)​=m/s

The m/s (meters per second) is therefore a derived unit. Similarly, the unit for Force, the Newton (N), is derived from the units of mass, length, and time: N=kg⋅m/s2. The concept of derived units allows the entire system of physical measurement to be consistently and coherently linked back to a small set of defined base units.

Question 9.

Define Standard metre.

Ans: 

The modern definition of the metre (m), the SI base unit for length, is tied to a fundamental constant of nature to guarantee extreme precision and universality. The Standard Metre is currently defined as:

This definition is unique and highly stable for the following key reasons:

1. Fixed Speed of Light: It effectively fixes the numerical value of the speed of light (c) at exactly 299,792,458 meters per second (m/s). The metre is thus not defined by a physical object (like an old metal bar) but by this universal constant.
2. Universal Reproducibility: Since the speed of light is constant everywhere, the definition ensures that the standard for the metre is universally available and highly reproducible with high accuracy.
3. Dependence on Time: The accuracy of the metre is now inherently linked to the accuracy of the SI base unit for time, the second. The second is itself defined using another unchanging atomic constant (the frequency of the cesium-133 atom).

Question 10.

Name two units of length which are bigger than a metre. How are they related to the metre?

Ans:

Two units of length that are significantly bigger than a metre are the Kilometre and the Astronomical Unit.

1. Kilometre (km):
   • The kilometre is the standard unit used for measuring large terrestrial distances, such as the distance between cities or the length of a road.
   • Relation to the Metre: A kilometre is equal to one thousand metres.
     
     1 km=1000 m
2. Astronomical Unit (AU):
   • The Astronomical Unit is a unit of distance used primarily for measuring distances within our solar system. It is defined as the average distance between the Earth and the Sun.
   • Relation to the Metre: One Astronomical Unit is approximately equal to 149.6 billion metres.
     
     1 AU≈1.496×1011 m

Question 11.

Write the names of two units of length smaller than a metre. Express their relationship with the metre.

Ans:

Two units of length smaller than a metre and their relationship with the metre are:

1. Centimetre (cm): One metre contains one hundred centimetres.
   1 cm=10−2 mor1 m=100 cm
2. Millimetre (mm): One metre contains one thousand millimetres.
   1 mm=10−3 mor1 m=1000 mm

Note: Other commonly used units smaller than a metre include the micrometre (μm) and the nanometre (nm).

Question 12.

How is nanometer related to Angstrom?

Ans:

The nanometer (nm) and the Angstrom (A˚) are both metric units of length used to measure extremely small distances, such as atomic dimensions and wavelengths of light. The relationship between them is straightforward: one nanometer is equal to ten Angstroms.

The conversion factors based on the standard unit, the meter (m), are:

• 1 nanometer (nm)=10−9 m
• 1 Angstrom (A˚)=10−10 m

Therefore, mathematically:

1 nm=10−10 m/A˚10−9 m​=10(−9)−(−10) A˚=101 A˚

This means the Angstrom is a smaller unit than the nanometer. While the nanometer is an official SI unit prefix, the Angstrom is a non-SI unit, though it is still commonly used in fields like crystallography and atomic physics because it conveniently expresses bond lengths and atomic radii.

Question 13.

Name the three convenient units used to measure length ranging from very short to very long value. How are they related to the S.I unit?

Ans:

The three convenient units of length used to measure values ranging from very short to very long, along with their relation to the S.I. unit (the meter, m), are:

Range	Unit Name (Symbol)	Used to Measure	Relation to S.I. Unit (Meter, m)
Very Short	Angstrom (A˚)	Atomic sizes, chemical bond lengths, and wavelengths of X-rays.	1 A˚=10−10 m
Intermediate	Centimeter (cm)	Everyday objects like the length of a pencil or a person’s height.	1 cm=10−2 m
Very Long	Light Year (ly)	Interstellar and astronomical distances (e.g., distance to stars).	1 ly≈9.46×1015 m

Relation to the S.I. Unit

The S.I. unit of length is the meter (m). All other units of length are defined in terms of the meter, either as decimal multiples/submultiples (using S.I. prefixes) or as separate non-S.I. units with a defined conversion factor.

1. Angstrom (A˚): This unit is a non-S.I. unit used for extremely small measurements. It is defined as exactly one ten-billionth of a meter.
   1 Angstrom=1×10−10 m
2. Centimeter (cm): This is a decimal submultiple of the S.I. unit, where the prefix centi- means one hundredth (10−2).
   1 Centimeter=1×10−2 m
3. Light Year (ly): This is a non-S.I. unit used for astronomical distances. It is defined as the distance light travels in a vacuum in one Julian year. When converted, its value is an extremely large multiple of the meter.
   
   1 Light Year≈9,460,730,472,580,800 m
   or 1 ly≈9.46×1015 m

Question 14.

Name the S.I unit of mass and define it.

Ans:

The kilogram (kg), the S.I. unit of mass, is now defined by fixing the exact numerical value of the Planck constant (h).

This modern definition sets the value of h as precisely 6.62607015×10−34 when expressed in the unit J⋅s (joule-second), which is equivalent to kg⋅m2⋅s−1. Because the values for the meter (m) and the second (s) are already established using other fundamental constants, the kilogram’s value is derived from this fixed constant. This connection is physically realized using a highly sophisticated weighing apparatus known as the Kibble balance . By basing the kilogram on a universal constant of nature, the standard is now universally stable and reproducible, overcoming the historical issue of relying on a fragile physical object (the International Prototype of the Kilogram) whose mass could change over time.

Question 15.

(a) Complete the following: 1 light year =……….m

(b) Complete the following: 1 m =……….Å

(c) Complete the following: 1 m  =……….. µ

(d) Complete the following: 1 micron =………..Å

(e) Complete the following: 1 fermi = ……….. M

Ans:

(a) 1 light year = 9.46×1015 m 

(b) 1 m = 1010 A˚ (Angstrom) 

(c) 1 m = 106 μ (micron)

(d) 1 micron (μ) = 104 A˚ (Angstrom) 

(e) 1 fermi (f) = 10−15 m

Question 16. 

State two units of mass smaller than a kilogram. How are they related to kilogram?

Ans:

Two units of mass that are smaller than a kilogram (kg) are the gram (g) and the milligram (mg).

Relation to Kilogram

1. Gram (g): The gram is one thousandth of a kilogram. This is based on the metric prefix ‘kilo’ which means 1000. The relationship is:
   1 gram=10001​ kilogramor1 g=10−3 kg
2. Milligram (mg): The milligram is one millionth of a kilogram. It is also one thousandth of a gram (the prefix ‘milli’ means 10−3). The relationship is:
   1 milligram=1,000,0001​ kilogramor1 mg=10−6 kg

Question 17. 

State two units of mass bigger than a kilogram. Give their relationship with the kilogram?

Ans:

Two units of mass larger than a kilogram (kg) are the Quintal and the Metric Tonne.

Here is their relationship with the kilogram:

1. Quintal (q)
   • Relationship: One quintal is equivalent to 100 kilograms.
   • Formula: 1 q=100 kg
2. Metric Tonne (t)
   • Relationship: One metric tonne is equivalent to 1000 kilograms.
   • Formula: 1 t=1000 kg

The Metric Tonne is often used to measure the mass of large, bulk commodities in trade and industry, such as grains, metals, or vehicle cargo.

Question 18. 

(a)Complete the following: 1 g =………kg 

(b) Complete the following : 1 mg =………kg 

(c) Complete the following: 1 quintal =………kg 

(d)Complete the following : 1 a.m.u (or u) =……..kg

Ans:

Unit	Conversion to Kilogram (kg)
(a) 1 g	10−3 kg
(b) 1 mg	10−6 kg
(c) 1 quintal	100 kg
(d) 1 a.m.u (or u)	1.6605×10−27 kg

Question 19. 

Name the S.I unit of time and define it.

Ans:

The modern definition of the second (s), the S.I. unit of time, is based on a fundamental and unchanging atomic property, which ensures its exceptional accuracy and universal consistency.

One second is formally defined as the duration of exactly 9,192,631,770 periods of the radiation produced by the transition between the two specific hyperfine energy levels of an unperturbed Caesium-133 atom in its ground state. This definition effectively fixes the numerical value of the Caesium-133 transition frequency (ΔνCs​) at 9,192,631,770 Hertz (Hz), where Hz is equivalent to s−1. By referencing a constant of nature—the resonant frequency of the Caesium-133 atom—the second is made the most stable and accurately measurable of all the fundamental S.I. units.

Question 20.

Name two units of time bigger than a second. How are they related to the Second?

Ans:

Two units of time that are bigger than a second (s) are the minute (min) and the hour (h).

Their relationship to the second, which is the SI base unit of time, is as follows:

1. Minute (min):
   • One minute is defined as a duration of 60 seconds.
   • Relation to Second: 1 min=60 s
2. Hour (h):
   • One hour is defined as a duration of 60 minutes.
   • Since 1 minute is 60 seconds, one hour is equal to 60×60=3600 seconds.
   • Relation to Second: 1 h=3600 s

Question 21. 

What is a leap year?

Ans:

A leap year is a calendar year that contains an extra day, making it 366 days long instead of the usual 365. This additional day, known as a leap day, is added to the month of February, extending it to February 29th. The purpose of a leap year is to keep our civil calendar synchronized with the solar year (the actual time it takes the Earth to complete one full orbit around the Sun).

The Earth’s orbit takes approximately 365.2422 days (or about 365 days and 6 hours). If we only used a 365-day year, we’d lose roughly six hours every year. Over a century, the calendar would drift by about 24 days, causing seasons to gradually fall out of alignment with the calendar dates. By adding a leap day almost every four years, we largely correct this accumulated discrepancy, ensuring that the seasons begin consistently around the same time each year.

The rules for determining a leap year under the Gregorian calendar (the one used by most of the world) are:

1. A year is a leap year if it is evenly divisible by 4 (e.g., 2024, 2028).
2. Exception 1: If the year is evenly divisible by 100, it is not a leap year (e.g., 1700, 1800, 1900).
3. Exception 2: If the year is evenly divisible by 400, it is a leap year (e.g., 1600, 2000, 2400).

This set of rules results in an average year length of 365.2425 days, which is extremely close to the true solar year, keeping the calendar accurate for centuries.

Question 22.

The year 2020 will have February of 29 days’. Is this statement true?

Ans:

The statement, “The year 2020 will have February of 29 days,” is True. 

Explanation

The year 2020 was a Leap Year, which means it had 366 days instead of the usual 365. This extra day is added to the calendar by extending the month of February from 28 days to 29 days.

The rules of the Gregorian calendar determine a leap year:

1. A year is typically a leap year if it is evenly divisible by 4 (which 2020÷4=505, a whole number).
2. Exception 1: Years divisible by 100 (like 1900 or 2100) are not leap years…
3. Exception 2: …unless they are also divisible by 400 (like 2000 or 2400), in which case they are leap years.

Since 2020 is divisible by 4 but not by 100, it satisfied the primary rule for a leap year, confirming that its February contained the extra day, February 29th.

Question 23.

What is a lunar month?

Ans:

A lunar month is a unit of time that is based on the Moon’s motion and its cycle of phases.

The most common and practical definition of a lunar month is the synodic month (or lunation), which is the average time it takes for the Moon to complete one cycle of its visible phases—for example, from one New Moon to the next.

Key Facts about the Lunar Month (Synodic Month)

• Duration: The average length of a synodic month is approximately 29.53 days (specifically, 29 days, 12 hours, 44 minutes, and 3 seconds).
• Basis: This duration is determined by the alignment of the Moon, Earth, and Sun. Because the Earth is constantly orbiting the Sun, the Moon has to travel an extra distance in its orbit after completing a full revolution around the Earth to “catch up” and return to the same alignment (i.e., the same phase, like New Moon).
• Calendars: Lunar calendars (like the Islamic Hijri calendar) and lunisolar calendars (like the Chinese and Jewish calendars) base their months on this cycle, typically alternating between 29 and 30 days to closely match the average 29.5 days.

Other Astronomical Lunar Months

In astronomy, there are several other precise definitions of a “month” based on different reference points:

• Sidereal Month: The time it takes for the Moon to complete one full orbit around the Earth when measured against the background of fixed stars. This is shorter than the synodic month, lasting about 27.32 days.
• Anomalistic Month: The time it takes for the Moon to return to its closest point to Earth (perigee). This cycle is important for determining the size and intensity of tides and phenomena like a Supermoon, lasting about 27.55 days.
• Draconic Month: The time it takes for the Moon to pass through the same orbital node (the points where the Moon’s orbit crosses the Earth’s orbital plane). This period is crucial for predicting eclipses and lasts about 27.21 days.

Question 24. 

(a) Complete the following: 1 nano second =……….s.

(b) Complete the following: 1 µs =……….s 

(c) Complete the following: 1 mean solar day = _______ s.

(d) Complete the following: 1 year =……….s.

Ans:

Conversion	Value in Seconds (s)
(a) 1 nano second (ns)	10−9 s
(b) 1 microsecond (μs)	10−6 s
(c) 1 mean solar day	86,400 s
(d) 1 year (≈365 days)	31,536,000 s (≈3.15×107 s)

Question 25. 

(a) Name the physical quantities which are measured in the given units:- u 

(b) Name the physical quantities which are measured in the given units:- ly 

(c) the physical quantities which are measured in the given units:- ns

(d) Name the physical quantities which are measured in the given units:- nm

Ans: 

Unit	Physical Quantity Measured
(a) u (or amu)	Mass (specifically, atomic/molecular mass)
(b) ly (Light Year)	Length or Distance (specifically, astronomical distances)
(c) ns (nanosecond)	Time
(d) nm (nanometer)	Length

Question 26. 

(a) Write the derived unit of speed

(b) Write the derived unit of force

(c) Write the derived unit of work

(d) Write the derived unit of the pressure

Ans:

The derived units in the International System of Units (SI) for the given quantities are:

Quantity	Derived Unit (Special Name)	Derived Unit (in Base Units)
(a) Speed	None (N/A)	metre per second (m/s or m⋅s−1)
(b) Force	Newton (N)	kilogram metre per second squared (kg⋅m/s2 or kg⋅m⋅s−2)
(c) Work	Joule (J)	kilogram metre squared per second squared (kg⋅m2/s2 or N⋅m)
(d) Pressure	Pascal (Pa)	kilogram per metre per second squared (kg/(m⋅s2) or N/m2)

Explanation

Derived units are defined by multiplying or dividing SI base units (like metre, kilogram, second) according to the physical formula:

• Speed: Speed=Distance/Time. The unit is metre/second.
• Force: Force=Mass×Acceleration. Since Acceleration is m/s2, the unit is kg⋅m/s2, which is named the Newton (N).
• Work: Work=Force×Distance. The unit is Newton×metre (N⋅m), which is named the Joule (J).
• Pressure: Pressure=Force/Area. The unit is Newton/metre2 (N/m2), which is named the Pascal (Pa).

Question  27.

(a) How are the following derived units related to the fundamental unit?

Newton

(b) How are the following derived units related to the fundamental unit?

watt

(c) How are the following derived units related to the fundamental unit?

joule

(d) How are the following derived units related to the fundamental unit?

Pascal

Ans: 

Derived Unit	Quantity	Relationship to Fundamental Units	Formula Basis
(a) Newton (N)	Force	kg⋅m⋅s−2	Force=mass×acceleration
(b) Watt (W)	Power	kg⋅m2⋅s−3	Power=timework​
(c) Joule (J)	Energy or Work	kg⋅m2⋅s−2	Work=force×distance
(d) Pascal (Pa)	Pressure	kg⋅m−1⋅s−2	Pressure=areaforce​

Question  28. 

(a) Name the physical quantity related to the following unit :- km2

(b) Name the physical quantity related to the following unit:-Newton

(c) Name the physical quantity related to the following unit :- Joule

(d) Name the physical quantity related to the following unit: Pascal

(e) Name the physical quantity related to the following unit:- watt

Ans:

(a) km2 is the unit for Area (km2 stands for square kilometre). 

(b) Newton (N) is the unit for Force.

(c) Joule (J) is the unit for Energy or Work. 

(d) Pascal (Pa) is the unit for Pressure. 

(e) Watt (W) is the unit for Power.

Exercise 1 (A)

Question 1. 

The fundamental unit is:-

1. Newton
2. Pascal
3. hertz
4. second

Question 2.

Which of the following unit is not a fundamental unit:

1. metre
2. Litre
3. second
4. kilogram

Question 3.

The unit of time is :

1. light year
2. parsec
3. leap year
4. angstrom

Question 4.

1 Å is equal to :

1. 0.1 nm
2. 10-10 cm
3. 10-8 m
4. 104 µ

Question 5.

ly is the unit of:-

1. time
2. length
3. mass
4. none of this

*******Exercise 1 (A)

Question 1.

(a) The wavelength of light of a particular colour is 5800 Å. Express it in nanometre.

(b)The wavelength of light of a particular colour is 5800 Å. Express it in metre.

Ans:

The wavelength of light is 5800 A˚. Here are the conversions:

(a) Expressed in Nanometres (nm)

The relationship is 1 A˚=0.1 nm.

Wavelength=5800 A˚=580 nm

(b) Expressed in Metres (m)

The relationship is 1 A˚=10−10 m.

Wavelength=5800 A˚=5.8×10−7 m

(Calculation Note: 5800×10−10 m=5.8×103×10−10 m=5.8×10(3−10) m=5.8×10−7 m.)

Question 2.

The size of bacteria is 1 µ. Find the number of bacteria present in 1 m length.

Ans:

The total number of bacteria that fit along the 1 m length is 106, or one million.

Question 3.

The distance of a galaxy is 5·6 × 1025 m . Assuming the speed of light to be 3 × 108 ms−1. Find the time taken by light to travel this distance . 

[Hint : Time taken = Distance travelled speed

Ans:

The time (t) light takes to cover a specific distance (D) is fundamentally calculated by dividing that distance by the speed of light (v), following the basic formula:

t=vD​

Given Parameters

• Distance to the Galaxy (D): 5.6×1025 m
• Speed of Light (v): 3×108 m/s

Step-by-Step Calculation

The values are substituted into the formula for time:

t=3×108 m/s5.6×1025 m​

To simplify, the numerical coefficients are separated from the powers of ten:

t=(35.6​)×10(25−8) s

Performing the division and simplifying the exponent yields:

t≈1.866…×1017 s

Final Conclusion

The calculated time required for light to travel the distance of 5.6×1025 m is approximately 1.87×1017 seconds.

This incredibly long duration is immense, translating to nearly 5.9 billion years, highlighting the vast scale of astronomical distances.

Question 4.

The wavelength of light is 589 nm. What is its wavelength in Å?

Ans:

The wavelength of the light, λ, is 589 nm. To find its value in A˚ (Angstrom), we use the established conversion factor between nanometers (nm) and Angstroms (A˚).

Conversion Factor

Both the nanometer and the Angstrom are units used to measure extremely small lengths, such as the wavelength of light. Their relationship is:

1 nm=10 A˚

Calculation

To convert the wavelength from nm to A˚, we multiply the value by 10:

λ=589 nmλ=589×10 A˚λ=5890 A˚

Result

The wavelength of light is 5890 A˚.

Question 5.

The mass of an oxygen atom is 16.0 u. Express it in kg.

Ans:

The mass of the oxygen atom, 16.0 u, can be expressed in kilograms (kg) using the conversion factor for the unified atomic mass unit (u).

Conversion

The relationship between the atomic mass unit (u) and the kilogram (kg) is:

1 u≈1.661×10−27 kg

Calculation

To find the mass in kilograms, multiply the given mass in u by the conversion factor:

Mass in kg=16.0 u×(1.661×10−27 ukg​)

Mass in kg≈2.658×10−26 kg

Rounding to three significant figures, the same as the input mass:

Mass in kg≈2.66×10−26 kg

The mass of an oxygen atom is approximately 2.66×10−26 kilograms.

Question 6. 

It takes 8 min for light to reach from the sun to the earth surface . If the speed of light is taken to be 3 ×108  m/s−1 , find the distance from the sun to the earth in km .

Ans:

Here is the calculation to determine the distance from the Sun to the Earth, based on the travel time of light.

The fundamental relationship governing this calculation is: Distance=Speed×Time.

1. Standardize the Time Unit (Minutes to Seconds) 

To ensure dimensional consistency with the speed of light (which is given in meters per second), the travel time must be converted from minutes to seconds:

Time (t)=8 minutes×60 minute seconds​=480 seconds

2. Compute the Distance in Meters (m)

Using the established values: the time (t=480 s) and the speed of light (v=3×108 m/s):

D=v×tD=(3×108 m/s)×480 sD=1440×108 m

D=1.44×1011 m

3. Convert Distance to Kilometers (km)

The final distance is required in kilometers, so the value in meters is divided by 1000 (since 1 km=1000 m):

Dkm​=103 m/km1.44×1011 m​Dkm​=1.44×10(11−3) kmDkm​=1.44×108 km

The distance between the Sun and the Earth is 1.44×108 kilometers (or 144 million kilometers).

Question 7. 

‘The distance of a star from the earth is 8.33 light minutes.’ What do you mean by this statement? Express the distance in meters.

Ans:

This statement, ‘The distance of a star from the earth is 8.33 light minutes,’ means that light, traveling at its tremendous speed, takes 8.33 minutes to cover the distance between that star and the Earth.

It is defined as the distance light travels in a vacuum over the course of one minute. This unit is used to express vast astronomical distances in a way that is easier to grasp than using excessively large numbers of kilometers or miles.

Distance in Meters

To express this distance in meters, we use the formula:

Distance(D)=Speed of Light(v)×Time(t)

We need to use the standard SI units for this calculation, so we’ll use:

• Speed of light (v): 3.00×108 m/s
• Time (t): 8.33 minutes

1. Convert Time to Seconds

First, convert the time from minutes to seconds:

t=8.33 min×60 mins​=499.8 s

2. Calculate Distance

Now, substitute the values into the distance formula:

D=(3.00×108 m/s)×499.8 s

D=1499.4×108 m

3. Express in Scientific Notation

Finally, convert the result to standard scientific notation:

D=1.50×1011 m

The distance of the star from the Earth is approximately 1.50×1011 meters.

Exercise 1 (B)

Question 1. 

Explain the meaning of the term ‘least count of an instrument’ by taking a suitable example.

Ans:

The Least Count (LC) of an instrument is the smallest measurement that can be accurately measured or resolved by that instrument. It represents the precision of the measuring device.

In simpler terms, it is the value of the smallest division marked on the instrument’s scale. Any measurement taken using that instrument can only be considered reliable up to that minimum value.

Example: A Standard Meter Ruler

A common plastic or wooden ruler is a good example of how least count is determined.

Instrument Details

• Main Scale Divisions: A standard meter ruler is typically marked with centimeters (cm) and millimeters (mm).
• The space between two consecutive centimeter markings is 1 cm.
• Each centimeter is further divided into smaller markings, which are millimeters. The smallest interval between two adjacent markings on the ruler is 1 mm.

Least Count

The least count of the ruler is the value of its smallest division:

Least Count (LC)=1 mm or 0.1 cm

Implication

This means that when using a standard ruler:

1. You can confidently measure a length, say, to 15.3 cm.
2. You cannot accurately measure a length like 15.35 cm because the instrument lacks the resolution (the smallest division) to resolve the second decimal place (the 0.05 cm or 0.5 mm value).
3. Any recorded measurement will have an uncertainty equal to the least count (e.g., 15.3 cm±0.1 cm).

A smaller least count indicates a more precise instrument (e.g., a Vernier caliper has a LC of 0.1 mm, making it ten times more precise than a standard ruler).

Question 2. 

A boy makes a ruler with graduations in cm on it, (i.e. 100 divisions in 1 m). To what accuracy  can this ruler measure? How can this accuracy be increased?

Ans:

The accuracy (specifically, the precision) to which a ruler can measure is determined by its Least Count (LC), which is the value of its smallest graduation.

1. Measurement Accuracy

The ruler has 100 divisions in 1 m (or 100 cm).

• Length of the smallest division (Least Count):
  LC=Number of DivisionsTotal Length​=100100 cm​=1 cm
• Accuracy: The ruler can measure with an accuracy of ±1 cm. This means any measurement taken with it can only be reliably estimated to the nearest centimeter.

2. Increasing Accuracy

The accuracy of this ruler can be increased by reducing its least count.

• Method: To reduce the least count, the boy must increase the number of graduations (divisions) within the 1 m length.
• Example: If the boy marks 1000 divisions in 1 m (i.e., marking every millimeter), the new least count would be:
  New LC=1000100 cm​=0.1 cm (or 1 mm)

This new ruler would measure to an accuracy of ±0.1 cm, which is ten times greater than the original ruler.

Question 3.

A boy measures the length of a pencil and expresses it to be 2.6 cm. What is the accuracy of his measurement? Can he write it as 2.60 cm?

Ans:

The accuracy of the boy’s measurement of 2.6 cm is determined by the precision of the instrument he used, which is indicated by the number of decimal places recorded.

Accuracy of Measurement

The measurement 2.6 cm has two significant figures, with the last digit (the 6) being the estimated one. Assuming he used a standard centimetre ruler or scale (which typically has divisions up to the 1 mm mark, or 0.1 cm), the least count of the instrument would be 0.1 cm.

The accuracy (or more precisely, the absolute error or uncertainty) is usually taken as half the least count for readings taken between the marks, or ± the full least count for readings taken directly on a mark. In this context, the reading 2.6 cm implies that the measurement is accurate to the first decimal place:

Accuracy=±0.1 cm

This means the actual length of the pencil lies between 2.5 cm and 2.7 cm.

Can he write it as 2.60 cm?

No, he cannot write the measurement as 2.60 cm.

• Writing 2.60 cm implies an accuracy of ±0.01 cm (one-hundredth of a centimetre), meaning the measuring instrument has a least count of 0.01 cm (or 0.1 mm), such as a Vernier Callipers.
• Since his initial reading of 2.6 cm only expresses accuracy to the 0.1 cm place, adding the final zero (2.60) would incorrectly suggest that he used a more precise instrument, like a Vernier Callipers, and that he is certain the length is exactly 2.60 cm and not, for example, 2.59 cm or 2.61 cm.

Question 4. 

Define the least count of vernier callipers. How do you determine it?

Ans:

The Least Count (LC) of a Vernier Callipers is the smallest distance or length that can be accurately measured using the instrument. It represents the limit of the instrument’s precision. 

Determining the Least Count

The Least Count is calculated using the difference between the smallest division on the main scale and the smallest division on the Vernier scale.

The formula to determine the Least Count is:

LC=1 MSD−1 VSD

Where:

• MSD is the value of one Main Scale Division (the smallest marking on the main scale).
• VSD is the value of one Vernier Scale Division (the value corresponding to the smallest marking on the Vernier scale).

In practice, VSD is often not directly known. The LC is more practically calculated using the following derived formula:

LC=Total number of divisions on the Vernier scaleValue of the smallest Main Scale Division​

If, for example, 10 Vernier Scale Divisions (VSD) are equal in length to 9 Main Scale Divisions (MSD), and the MSD value is 1 mm, the calculation is:

LC=101 mm​=0.1 mm or 0.01 cm

Question 5.

Define the term ‘Vernier constant’.

Ans:

The term ‘Vernier constant’ is synonymous with the Least Count (LC) of a Vernier Callipers.

The Vernier Constant is defined as the difference between the value of one Main Scale Division (1 MSD) and the value of one Vernier Scale Division (1 VSD).

It represents the smallest distance or length that can be accurately measured by the Vernier Callipers. 

Formula

The Vernier Constant (VC) is mathematically expressed as:

VC=1 MSD−1 VSD

Alternative Definition

In practical terms, it is the ratio of the smallest division on the main scale to the total number of divisions on the Vernier scale:

VC=Total number of divisions on Vernier ScaleSmallest value on Main Scale​

Question 6.

When is a vernier Callipers said to be free from zero error?

Ans:

A Vernier Callipers is said to be free from zero error when the zero mark of the Vernier scale perfectly coincides with the zero mark of the Main scale when the jaws of the callipers are brought into gentle contact.

In this ideal condition, the instrument registers a reading of exactly zero when the measured object’s size is zero. If any other Vernier scale mark coincides, or if the zeros do not align, a zero error is present.

Question 7.

What is meant by zero error of vernier callipers ? How is it determined? Draw neat diagrams to explain it. How is it taken in account to get the correct measurement?

Ans:

The Zero Error (ZE) of a Vernier Callipers is a systematic error that occurs when the jaws are fully closed, and the zero mark of the Vernier scale does not precisely align with the zero mark of the Main scale. This indicates the instrument has a built-in offset.

Types and Determination

Type of Zero Error	Alignment Condition	Determination of n	Zero Error (ZE) Formula
Positive (+ZE)	Vernier zero is to the right of the Main scale zero.	n = The coinciding Vernier Scale Division (VSD)	+ZE=+n×LC
Negative (−ZE)	Vernier zero is to the left of the Main scale zero.	n = The coinciding Vernier Scale Division (VSD)	−ZE=−(N−n)×LC (Where N is total $\text{VSD}$s)

Correction

To obtain the true measurement, a Zero Correction (ZC) is applied. The ZC is always the negative of the ZE:

Zero Correction (ZC)=−(Zero Error)

The Correct Reading is then found by:

Correct Reading=Observed Reading+Zero Correction

• If ZE is Positive (+n×LC), the ZC is Negative, so you subtract the error.
• If ZE is Negative (−(N−n)×LC), the ZC is Positive, so you add the correction.

Question 8.

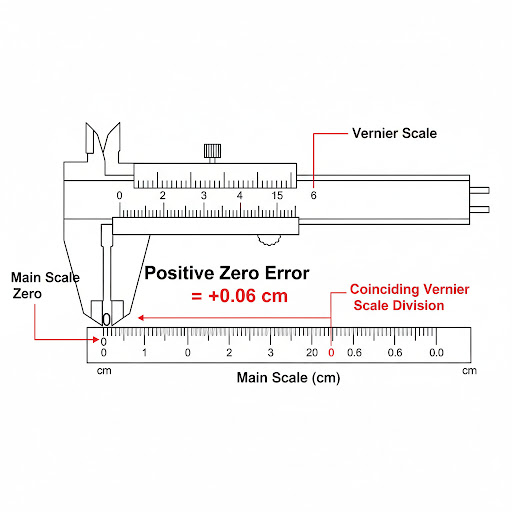
A vernier caliper has a zero error of + 0.06 cm. Draw a neat labelled diagram to represent it.

Ans:

A vernier caliper has a zero error of + 0.06 cm. Draw a neat labelled diagram to represent it.

Question 9.

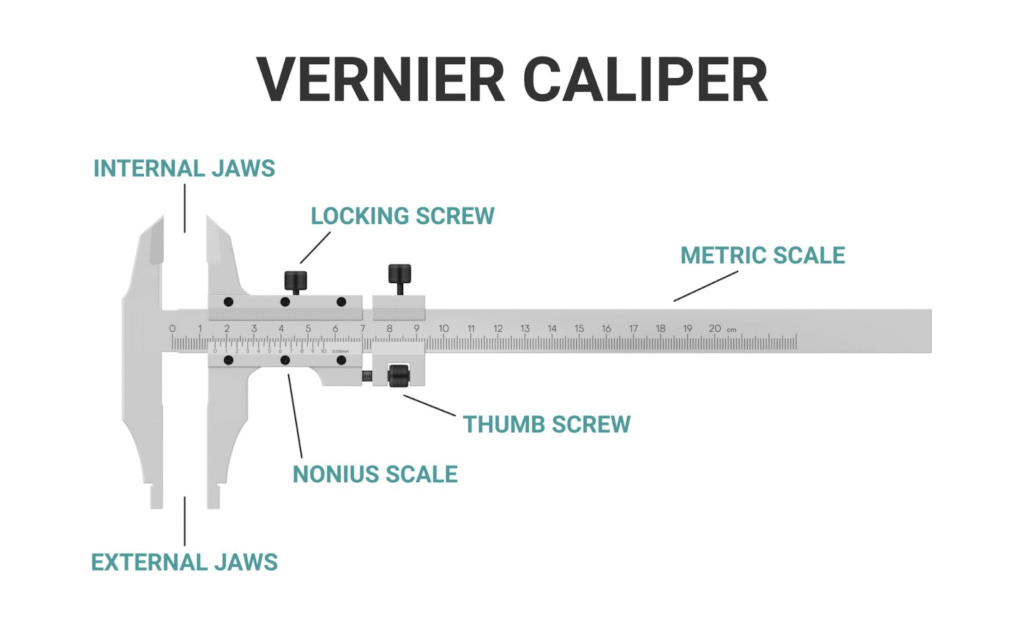
Draw a neat and labelled diagram of vernier callipers. Name its main parts and state their functions.

Ans:

Here are the main parts of a Vernier Callipers and their functions:

Main Parts and Functions:

1. Main Scale (Fixed):
   • Function: This is a fixed scale, typically graduated in centimeters and millimeters. It provides the primary reading of the measurement, similar to a ruler.
2. Vernier Scale (Movable):
   • Function: This scale slides along the main scale. It has divisions that are slightly smaller than the main scale divisions, allowing for more precise readings than the main scale alone. It helps determine the fractional part of the smallest main scale division.
3. External Measuring Jaws (Lower Jaws):
   • Function: These are the larger, flat jaws used to measure the external diameter or width of an object. The object is placed between these jaws.
4. Internal Measuring Jaws (Upper Jaws):
   • Function: These are the smaller, pointed jaws used to measure the internal diameter of hollow objects (like the inside of a pipe or a beaker).
5. Depth Bar/Rod (or Depth Probe):
   • Function: This thin rod extends from the end of the movable jaw as it slides. It is used to measure the depth of holes or steps in an object.
6. Locking Screw:
   • Function: Once an object is correctly positioned and the jaws are set, this screw is tightened to fix the movable jaw in place, preventing it from slipping and ensuring an accurate reading can be taken.
7. Fine Adjustment Screw:
   • Function: On some Vernier Callipers, this screw is used for making very small, precise movements of the movable jaw to ensure accurate contact with the object being measured.

Question 10.

State three uses of the vernier callipers.

Ans:

Vernier callipers are essential tools for precise dimensional measurement in science, engineering, and workshops. They are highly valued for their versatility, as they can perform three distinct types of measurements on an object: 

1. Outer Dimensions: They measure the external length, width, or diameter of a solid object (like a rod or block) by clamping it between the two large, main jaws.
2. Inner Dimensions: They accurately determine the internal diameter (or bore) of a hollow object (such as a tube or container) using the smaller, upper jaws.
3. Depth: They measure the depth of a recess or a blind hole using the thin measuring strip or tail that extends from the back end of the instrument’s main body.

Question 11.

Name the two scales of vernier callipers and explain how it is used to measure length correctly up to 0.01 cm.

Ans:

The two scales of a Vernier Callipers are the Main Scale and the Vernier Scale.

I. The Two Scales

1. Main Scale (MS): This is the fixed scale on the main body of the instrument. It is marked like a standard ruler, typically graduated in centimeters (cm) with the smallest division being 1 mm (or 0.1 cm). This scale provides the initial reading.
2. Vernier Scale (VS): This is the sliding scale attached to the movable jaw. It is a shorter scale with divisions that are slightly smaller than the divisions on the main scale. Its purpose is to provide an accurate fraction of the smallest Main Scale Division, increasing the instrument’s precision.

II. Measuring Length up to 0.01 cm

The ability to measure accurately up to 0.01 cm is due to the instrument’s Least Count (LC).

Least Count (LC)=0.01 cm

This precision is achieved because the Vernier Scale is constructed so that a specific number of its divisions (N) match (N−1) divisions on the Main Scale. For a standard metric Vernier Callipers, 10 VSD often equal 9 MSD, and since 1 MSD=0.1 cm:

LC=1 MSD−1 VSD=Number of divisions on VSValue of 1 MSD​=100.1 cm​=0.01 cm

The Reading Procedure

The final length measurement (TR) is determined by combining the readings from both scales:

Total Reading (TR)=MSR+(VSC×LC)

1. Main Scale Reading (MSR): This is the reading on the Main Scale immediately before the zero mark of the Vernier Scale. This gives the measurement up to the first decimal place (e.g., 2.3 cm).
2. Vernier Scale Coincidence (VSC): This is the number of the division on the Vernier Scale that exactly aligns with any division on the Main Scale.
3. Fractional Part: The VSC is multiplied by the Least Count (0.01 cm) to get the fractional part of the measurement (e.g., if VSC=4, the fractional part is 4×0.01=0.04 cm).
4. Final Result: The MSR and the fractional part are added to give the final reading with two decimal places of precision (e.g., 2.3 cm+0.04 cm=2.34 cm).

This method allows the user to accurately resolve a distance that is smaller than the smallest division on the main scale.

Question 12. 

Describe in steps, how would you use vernier callipers to measure the length of a small rod?

Ans:

1. Preparation and Zero Error Check

1. Determine Least Count (LC): Find the smallest distance the caliper can measure. This is usually LC=Number of Vernier Scale DivisionsSmallest Main Scale Division​.
2. Check Zero Error: Gently close the external measuring jaws until they touch.
   • If the zero mark of the Vernier Scale (VS) perfectly aligns with the zero mark of the Main Scale (MS), there is no zero error.
   • If they do not align, note the zero error (Z) and its sign (positive or negative) for correction later.

2. Taking the Measurement

1. Position the Rod: Loosen the locking screw and slide the movable jaw open. Place the rod snugly between the external measuring jaws (the larger, lower jaws). The rod’s length should be aligned with the body of the caliper.
2. Secure the Rod: Gently slide the movable jaw until the jaws make firm, but not excessively tight, contact with the ends of the rod. Lock the movable jaw in place using the clamping screw.
3. Read the Main Scale (MSR): Observe the position of the zero mark of the Vernier Scale. The Main Scale Reading (MSR) is the value of the last division on the main scale that is fully visible immediately to the left of the Vernier Scale zero mark.

3. Reading and Calculation

1. Read the Vernier Scale (VSR): Look carefully along the Vernier Scale and identify the division line that exactly coincides (lines up perfectly) with any division line on the Main Scale. Note the number of this coinciding division (N). This is the Vernier Scale Coinciding Division.
2. Calculate Vernier Scale Reading (VSR): The VSR is calculated by multiplying the coinciding division number (N) by the Least Count (LC).
   VSR=N×LC
3. Calculate Observed Length (Lobs​): Add the Main Scale Reading (MSR) and the Vernier Scale Reading (VSR).
   Lobs​=MSR+VSR
4. Calculate True Length (Ltrue​): Apply the zero correction to the observed length.
   Ltrue​=Lobs​−(Zero Error)
   (Note: If the zero error is positive, you subtract; if the zero error is negative, subtracting the negative value is the same as adding the magnitude).
5. Repeat: Take the measurement at least three times at different points along the rod (if possible) and calculate the average true length for maximum accuracy.

Question 13. 

(a) Name the part of the vernier callipers which is used to measure the following

External diameter of a tube 

(b) Name the part of the vernier callipers which is used to measure the following

Internal diameter of a mug 

(c) Name the part of the vernier callipers which is used to measure the following

Depth of a small bottle 

(d) Name the part of the vernier callipers which is used to measure the following

Thickness of a pencil.

Ans:

The Vernier Caliper is a versatile precision instrument designed to measure various dimensions of an object. Here are the specific parts used for the measurements listed:

(a) External diameter of a tube

The part used is the Lower Jaws (or External Measuring Jaws). These large jaws are used to grip the outside surfaces of an object to measure its length or external diameter.

(b) Internal diameter of a mug

The part used is the Upper Jaws (or Internal Measuring Jaws). These smaller jaws are inserted inside a hollow object (like a mug or a tube) and expanded to measure the inner diameter.

(c) Depth of a small bottle

The part used is the Depth Measuring Blade (or Depth Rod). This thin rod extends from the back end of the main scale as the jaws are opened and is lowered into a cavity (like a bottle or a hole) to measure its depth.

(d) Thickness of a pencil

The part used is the Lower Jaws (or External Measuring Jaws). Just like the external diameter, the thickness of a pencil is an external dimension measured by clamping the object between these two jaws.

Question 14.

(a) Explain the terms : Pitch . How are they determined?

(b) Explain the terms : Least count of a screw gauge. How are they determined?

Ans:

(a) Pitch of the Screw Gauge

The Pitch of a screw gauge is the linear distance moved by the screw (spindle) along the main scale when the circular scale (thimble) is given one complete rotation (360$^\circ$).

Determination of Pitch

The pitch is determined by:

1. Noting a starting position on the main scale.
2. Giving the circular scale a certain number of full rotations (N, typically 5 or 10).
3. Observing the total linear distance (D) moved by the screw on the main scale for these N rotations.
4. The pitch (P) is then calculated as:
   Pitch (P)=Number of full rotations (N)Distance moved on the Main Scale (D)​

• For most standard laboratory screw gauges, the pitch is 1 mm or 0.5 mm.

(b) Least Count of the Screw Gauge

The Least Count (LC) of a screw gauge is the smallest linear distance that can be accurately measured by the instrument. It is the distance the screw moves when the circular scale is rotated through one division.

Determination of Least Count

The least count is determined by dividing the Pitch by the total number of divisions on the circular scale.

Least Count (LC)=Total Number of Divisions on the Circular ScalePitch of the Screw Gauge​

• Example: If the Pitch is 1 mm and the circular scale has 100 divisions:
  LC=1001 mm​=0.01 mm
• The least count defines the precision of the instrument. Standard screw gauges typically have a least count of 0.01 mm (or 0.001 cm).

Question 15. 

How can the least count of a screw gauge be decreased?

Ans:

The least count (LC) of a screw gauge, which represents the smallest measurable distance, is determined by the following formula:

Least Count (LC)=Number of Divisions on the Circular Scale (N) / Pitch (P)​

To decrease the least count—thereby making the instrument more precise—one must either decrease the numerator (Pitch) or increase the denominator (Number of Circular Scale Divisions).

Methods to Decrease the Least Count

There are two primary ways to design a screw gauge with a smaller least count:

1. Decrease the Pitch of the Screw:
   • Pitch (P) is the linear distance the screw moves along the main scale for one complete rotation of the circular scale.
   • By using a finer screw thread, the pitch can be reduced (e.g., from 1 mm to 0.5 mm).
   • Effect: Since LC is directly proportional to P, reducing the pitch directly decreases the least count.
2. Increase the Number of Divisions on the Circular Scale:
   • The Circular Scale Divisions (N) are the markings around the circumference of the thimble. These commonly range from 50 to 100.
   • By increasing the total number of divisions (e.g., from 100 to 200) while keeping the pitch constant.
   • Effect: Since LC is inversely proportional to N, increasing the number of divisions directly decreases the least count.

For example, a standard screw gauge with a 1 mm pitch and 100 divisions has an LC of 1001 mm​=0.01 mm. If the number of divisions is increased to 200, the LC becomes 2001 mm​=0.005 mm, increasing the precision.

Question 16.

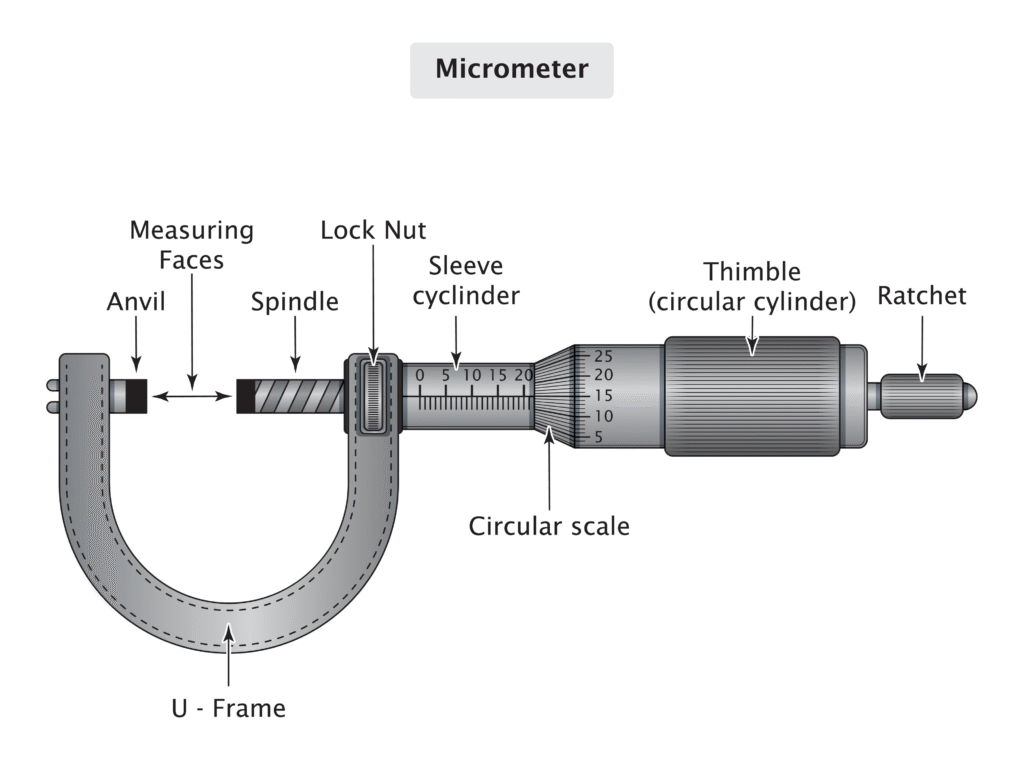
Draw a neat and labelled diagram of a screw gauge. Name its main parts and state their functions.

Ans:

Diagram of a Screw Gauge

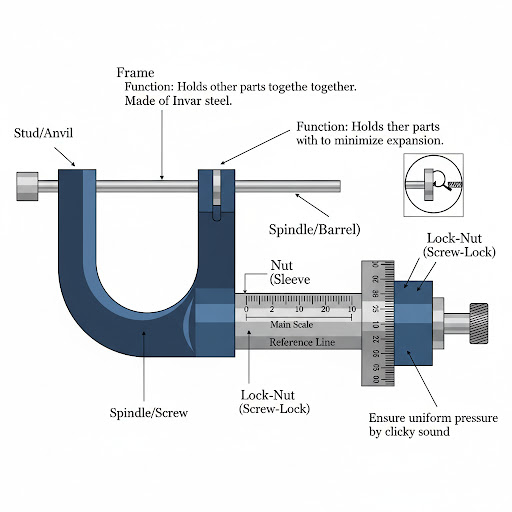
Main Parts and Their Functions

Here are the main components of a screw gauge and their respective functions:

1. U-Shaped Frame:
   • Function: This rigid, C-shaped metal frame holds all other parts of the screw gauge together. It’s often made of Invar steel or other low thermal expansion materials to minimize measurement errors due to temperature changes.
2. Stud (Anvil):
   • Function: A highly polished, flat-faced end attached to one side of the U-frame. It remains stationary and provides a fixed point against which the object to be measured is pressed by the spindle.
3. Spindle (Screw):
   • Function: A highly polished, flat-faced rod that moves perpendicularly towards or away from the stud. It has a precisely cut screw thread that engages with the nut (sleeve). The object to be measured is placed between the stud and the spindle.
4. Nut (Sleeve/Barrel):
   • Function: A hollow cylindrical part that is fixed to the U-frame. It contains the internal threading (nut) with which the spindle’s screw threads engage. The Main Scale (or Pitch Scale) is marked on the sleeve.
5. Main Scale (Pitch Scale):
   • Function: Marked along the length of the sleeve, usually in millimeters (mm). It measures the linear distance moved by the spindle when the thimble is rotated. Each division typically represents 1 mm or 0.5 mm.
6. Thimble (Head):
   • Function: A hollow cylinder that fits over the sleeve and rotates the spindle. Its beveled edge carries the Circular Scale (or Head Scale). As the thimble rotates, the spindle moves linearly.
7. Circular Scale (Head Scale):
   • Function: Marked around the circumference of the beveled edge of the thimble, typically divided into 50 or 100 equal parts. It is used to read fractional parts of the smallest main scale division, providing high precision.
8. Ratchet Stop:
   • Function: Located at the end of the thimble, this mechanism ensures that uniform pressure is applied to the object being measured, regardless of the user’s force. When the spindle touches the object and further rotation would apply excessive force, the ratchet slips with an audible “click,” preventing damage to the object or the instrument and ensuring repeatable readings.
9. Lock-Nut (Screw Lock):
   • Function: A small knurled nut located near the sleeve. Once the measurement is taken and the thimble is in position, the lock-nut can be tightened to prevent the spindle from moving, thereby preserving the reading while it’s being noted down.

Question 17.

State one use of a screw gauge.

Ans:

A key use of a screw gauge

is to accurately measure the diameter of thin wires.

It is a precision instrument designed to measure dimensions with an accuracy typically up to 0.01 mm (or 0.001 cm), which is vital for accurately determining the cross-sectional area of a wire in physics experiments.

The primary formula for reading a screw gauge is:

Total Reading=Main Scale Reading+(Circular Scale Reading×Least Count)±Zero Correction

The ability of the screw gauge to translate small linear displacements of the screw into much larger, readable rotations on the circular scale is what allows for this exceptional precision, making it superior to a Vernier caliper for measuring very small dimensions like the thickness of a sheet of paper or the diameter of a fine thread.

Question 18.

State the purpose of the ratchet in a screw gauge.

Ans:

The purpose of the ratchet (or ratchet stop) in a screw gauge is to ensure consistent and uniform measuring pressure is applied to the object.

Here’s a breakdown of its function:

1. Prevents Over-tightening: It acts as a safety device or limiting device. As you rotate the ratchet, it moves the spindle toward the object. Once the measuring faces make firm contact and the correct amount of force is reached, the ratchet mechanism will slip and produce a distinct clicking sound.
2. Ensures Accuracy: By clicking, it prevents the user from applying excessive force. This is critical because applying too much pressure can deform the object (especially if it is soft, like a thin metal sheet or paper), leading to an inaccurate measurement.
3. Standardizes Measurement: It makes measurements repeatable and consistent across different users. Regardless of the operator’s strength, the clicking sound confirms that the predetermined, correct pressure has been applied for a valid reading.

Question 19.

What do you mean by zero error of a screw gauge? How is it accounted for?

Ans:

The zero error of a screw gauge is the non-zero reading shown by the instrument when the measuring faces (the spindle and the anvil) are brought into contact with each other, meaning the actual distance being measured is zero.

In an ideal screw gauge, when the spindle and anvil touch, the zero mark of the circular scale should perfectly coincide with the datum line (or index line) of the main scale. If it doesn’t, there’s a zero error.

Types of Zero Error

There are two types of zero error, and the type depends on the position of the circular scale’s zero mark relative to the datum line.

Error Type	Condition (Zero mark of Circular Scale)	Formula for Zero Error (ZE)
Positive (+ZE)	Is below the datum line.	ZE=+(Coinciding Circular Scale Division×LC)
Negative (−ZE)	Is above the datum line.	ZE=−(Total Divisions−Coinciding Circular Scale Division)×LC

• LC stands for Least Count of the screw gauge.
• Total Divisions is typically 50 or 100, depending on the instrument.

How Zero Error is Accounted For

To obtain the Correct Reading (Actual Measurement), the zero error must be algebraically subtracted from the Observed Reading.

The correction is applied using the following formula:

Correct Reading=Observed Reading−Zero Error

This is equivalent to:

Correct Reading=Observed Reading+Zero Correction

where Zero Correction is simply the negative of the Zero Error (ZC=−ZE).

• For a Positive Zero Error (e.g., ZE=+0.03 mm): The correction is negative, so you subtract the value from the observed reading.
  Correct Reading=Observed Reading−(+0.03 mm)
• For a Negative Zero Error (e.g., ZE=−0.02 mm): The correction is positive, so you add the magnitude of the error to the observed reading.
  Correct Reading=Observed Reading−(−0.02 mm)=Observed Reading+0.02 mm

Question 20.

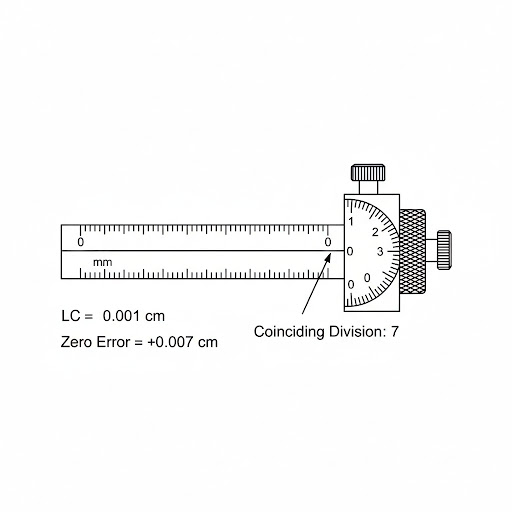
A screw gauge has a least count 0.001 cm and zero error +0.007 cm. Draw a neat diagram to represent it.

Ans:

Given:

• Least Count (LC) = 0.001 cm
• Zero Error (ZE) = +0.007 cm

A positive zero error means that when the measuring jaws are closed, the zero mark of the circular scale is below the datum line (or index line) of the main scale. The value of +0.007 cm tells us that the 7th division of the circular scale is coinciding with the datum line.

Here’s a diagram representing a screw gauge with a positive zero error of +0.007 cm:

Question 21.

What is a backlash error? Why is it caused? How is it avoided?

Ans:

A backlash error is a form of systematic error found in instruments that use a screw and nut mechanism, such as a screw gauge or spherometer.

What is Backlash Error?

Backlash error refers to the lost motion or delay in the movement of the measuring element (the spindle) when the direction of rotation of the thimble (or screw head) is suddenly reversed.

When you reverse the rotation, the thimble will turn by a small amount, but the spindle will remain stationary until the play or slack between the screw threads and the nut is taken up. This results in an inaccurate reading because the scale reading changes even though the physical position of the measuring tip has not moved for that portion of rotation.

Why is it Caused?

The primary cause of backlash error is wear and tear of the screw threads over time.

• Wear and Tear: Prolonged use causes the threads of the screw and the nut to wear down, which increases the clearance or gap (play) between them.
• Loose Fit: This clearance means that when the direction of rotation is changed, the screw has to rotate by a certain angle to bridge this gap before it can push or pull the nut (and thus the spindle) in the new direction.

How is it Avoided?

Backlash error cannot be corrected by an algebraic formula like zero error, but it can be avoided (or minimized) by adopting a specific measuring technique:

• Rotate in One Direction Only: For any single set of measurements (to measure the object and to find the reading), the screw should always be rotated in one direction—typically the direction that makes the spindle advance.
• If Direction Change is Necessary: If you accidentally overshoot the correct position and must reverse the rotation, you should turn the screw well beyond the final reading, stop, and then approach the final reading again by turning the screw in the desired (and consistent) direction. This ensures the screw threads are firmly engaged against one side of the nut’s threads when the final reading is taken.

Question 22.

Describe the procedure to measure the diameter of a wire with the help of a screw gauge.

Ans:

1. Determine the Screw Gauge Constants

First, find the two essential constants of the instrument:

• Pitch (P): The linear distance moved by the spindle for one complete rotation of the circular scale.
  P=Number of complete rotationsDistance moved by screw​
• Least Count (LC): The smallest distance that can be measured accurately with the screw gauge.
  LC=Total number of divisions on the circular scalePitch​

2. Check for and Record Zero Error

Before measuring the wire, check for instrumental error:

1. Bring the flat end of the screw (spindle) and the fixed stud (anvil) into contact by turning the ratchet head until it clicks gently (this ensures correct pressure).
2. Observe the position of the zero mark of the circular scale relative to the datum line (index line) of the main scale.
3. Calculate the Zero Error (ZE):
   • No Zero Error: If the zero mark of the circular scale coincides exactly with the datum line, then ZE=0.
   • Positive Zero Error (+ZE): If the zero mark is below the datum line, note the division (n) that coincides with the datum line.
     ZE=+(n×LC)
   • Negative Zero Error (-ZE): If the zero mark is above the datum line, note the division (m) that coincides with the datum line.
     ZE=−(Total Divisions−m)×LC

3. Measure the Diameter of the Wire

1. Place the Wire: Slightly open the jaws and place the wire between the spindle and the anvil, perpendicular to the main scale.
2. Tighten the Screw: Turn the ratchet head until the wire is gently but firmly held (listen for the clicks).
3. Record Readings:
   • Main Scale Reading (MSR): Note the reading on the main scale (pitch scale) that is just visible before the edge of the circular scale.
   • Circular Scale Reading (CSR): Note the circular scale division (C) that coincides with the datum line.
4. Calculate Observed Reading: The total observed reading (Diameter, Dobs​) is calculated as:
   Dobs​=MSR+(C×LC)
5. Repeat: Measure the diameter at several different points along the length of the wire, and at different orientations (by rotating the wire) to account for any non-uniformity. Calculate the average of these observed readings.

4. Apply Zero Correction

Finally, obtain the actual, correct diameter (Dcorrect​) by applying the zero correction to the average observed reading:

Dcorrect​=Dobs​−Zero Error

Question 23.

(a) Name the instrument which can accurately measure the following

The diameter of a needle

(b) Name the instrument which can accurately measure the following

The thickness of a paper

(c) Name the instrument which can accurately measure the following

The internal diameter of the neck of a water bottle

(d) Name the instrument which can accurately measure the following

The diameter of a pencil.

Ans:

Part	Object to be Measured	Instrument	Reason
(a)	The diameter of a needle	Screw Gauge (or Micrometer)	It has the highest precision (least count typically 0.001 mm or 0.01 mm), suitable for very small diameters.
(b)	The thickness of a paper	Screw Gauge (or Micrometer)	Paper is very thin, requiring the high precision of the screw gauge.
(c)	The internal diameter of the neck of a water bottle	Vernier Caliper	It is equipped with upper jaws specifically designed to measure internal diameters.
(d)	The diameter of a pencil	Vernier Caliper	It offers better precision (least count typically 0.1 mm or 0.01 cm) than a meter scale and is ideal for measuring small external diameters.

Question 24.

Which of the following measures a small length to high accuracy : metre rule , vernier callipers or screw gauge?

Ans:

he most accurate instrument among the metre rule, vernier callipers, and screw gauge for measuring small lengths is the screw gauge 🔩.

The degree of accuracy, or precision, in any measuring device is directly related to its least count (LC)—the smallest measurement unit the instrument can reliably read. A smaller least count signifies higher precision.

Here is a breakdown of the typical precision for the three instruments:

Instrument	Typical Least Count (LC)
Metre Rule	1 mm (or 0.1 cm)
Vernier Callipers	0.1 mm (or 0.01 cm)
Screw Gauge	0.01 mm (or 0.001 cm)

The screw gauge is the most precise because its least count of 0.01 mm is significantly smaller than that of the vernier callipers (0.1 mm) and the metre rule (1 mm). This high resolution allows it to measure dimensions like the diameter of a thin wire or the thickness of a paper sheet with the greatest fidelity.

Question 25.

(a) Name the instrument which has the least count 0.1 mm

(b) Name the instrument which has the least count 1 mm

(c) Name the instrument which has the least count 0.01 mm

Ans:

The instrument name for each specified least count is as follows:

(a) The instrument which has the least count of 0.1 mm (or 0.01 cm) is the Vernier Callipers.

(b) The instrument which has the least count of 1 mm (or 0.1 cm) is the Metre Rule (or a standard scale/ruler).

(c) The instrument which has the least count of 0.01 mm (or 0.001 cm) is the Screw Gauge (or Micrometer).

Exercise 1 (B)

Question 1. 

The least count of a vernier calipers is :

1. 1 cm
2. 0.001 cm
3. 0.1 cm
4. 0.01 cm

Question 2. 

A microscope has its main scale with 20 divisions in 1 cm and vernier scale with 25 divisions, the length of which is equal to the length of 24 divisions of main scale. The least count of microscope is

1. 0.002 cm
2. 0.001 cm
3. 0.02 cm
4. 0.01 cm

Question 3. 

The diameter of a thin wire can be measured by

1. A vernier calipers
2. A metre rule
3. A screw gauge
4. none of these

Exercise 1 (B)

Question  1. 

A stopwatch has 10 divisions graduated between the 0 and 5 s marks. What is its least count?

Ans:

The least count (LC) of an instrument is the smallest value that can be measured by it, which is the value of one division on its scale.

To find the least count of the stopwatch, we use the following formula:

Least Count=Number of Divisions in that IntervalValue of Smallest Graduated Interval​

From the given information:

• The interval is between the 0 s and 5 s marks, so the value of the smallest graduated interval is 5 s.
• The number of divisions graduated between these marks is 10.

Substituting these values:

Least Count=10 divisions5 s​=0.5 s/division

The least count of the stopwatch is 0.5 seconds.

Question  2.

A vernier has 10 divisions and they are equal to 9 divisions of the main scale in length. If the main scale is calibrated in mm, what is its least count?

Ans:

To find the Least Count (LC) of the Vernier Callipers, we use the relationship between the Vernier Scale Division (VSD) and the Main Scale Division (MSD).

Formula and Calculation

The least count of a Vernier Callipers is given by the formula:

LC=1 MSD−1 VSD

Alternatively, it can be calculated as:

LC=Number of divisions on Vernier ScaleSmallest division on Main Scale​

1. Given Values

• Smallest Main Scale Division (MSD): Since the main scale is calibrated in mm, the smallest division is 1 mm.
• Number of Vernier Scale Divisions (N): N=10 divisions.

2. Least Count Calculation

Using the simpler alternative formula:

LC=N1 MSD​LC=101 mm​LC=0.1 mm

Alternative Calculation (Using the relationship 10 VSD=9 MSD)

1. Find 1 VSD:
   10 VSD=9 MSD
   1 VSD=109​ MSD=0.9 mm
2. Apply the LC formula:
   LC=1 MSD−1 VSD
   LC=1 mm−0.9 mm
   LC=0.1 mm

The least count of the Vernier Callipers is 0.1 mm (or 0.01 cm).

Question  3. 

A microscope is provided with a main scale graduated with 20 divisions in 1 cm and a vernier scale with 50 divisions on it of length same as 49 divisions of main scale. Find the least count of the microscope.

Ans:

The least count of the microscope is 0.001 cm.

Here is the step-by-step calculation:

1. Determine the Value of One Main Scale Division (MSD)

The main scale is graduated with 20 divisions in 1 cm.

Value of 20 MSD=1 cm

Value of 1 MSD=201 cm​=0.05 cm

2. Determine the Least Count (LC) Formula

The least count for a vernier instrument is the difference between the value of one Main Scale Division and the value of one Vernier Scale Division (VSD).

LC=1 MSD−1 VSD

3. Relate MSD and VSD

The problem states that 50 divisions on the vernier scale have the same length as 49 divisions of the main scale:

50 VSD=49 MSD

Therefore, the value of one VSD is:

1 VSD=5049​ MSD

4. Calculate the Least Count (LC)

Substitute the value of 1 VSD into the least count formula:

LC=1 MSD−5049​ MSD

LC=(1−5049​) MSD

LC=(5050−49​) MSD

LC=501​ MSD

Now, substitute the numerical value for 1 MSD:

LC=501​×0.05 cm

LC=500.05 cm​

LC=0.001 cm

The least count of the microscope is 0.001 cm.

Question  4. 

A boy uses vernier callipers to measure the thickness of his pencil. He measures it to be 1.4 mm. If the zero error of vernier callipers is +0.02 cm, what is the correct thickness of the pencil?

Ans:

The final measurement is obtained by adjusting the initial reading for the instrument’s zero error. The relationship is expressed as:

Correct Measurement=Observed Reading−Zero Error

1. Unit Consistency

First, convert the observed reading to the desired final unit, centimeters (cm).

• Observed Reading (initial unit): 1.4 mm
• Conversion: 1.4 mm=1.4×0.1 cm=0.14 cm

2. Final Calculation

Substitute the measured values and the calculated positive zero error (ZE=+0.02 cm) into the correction formula:

Correct Thickness=0.14 cm−(+0.02 cm)Correct Thickness=0.14 cm−0.02 cmCorrect Thickness=0.12 cm

3. Result in Millimeters

To present the result with one decimal place in millimeters, convert the corrected value:

Correct Thickness=0.12 cm=0.12×10 mm=1.2 mm

The correct thickness of the pencil is 0.12 cm (or 1.2 mm).

Question  5. 

A vernier caliper has its main scale graduated in mm and 10 divisions on its vernier scale are equal in length to 9 mm. When the two jaws are in contact, the zero of the vernier scale is ahead of the zero of the main scale and the 3rd division of the vernier scale coincides with a main scale division.

Find : (i) The least count and

         (ii) The zero error of the vernier callipers.

Ans:

To solve this problem, we’ll first find the least count (LC) and then use the given information about the zero position to find the zero error (ZE).

(i) Least Count (LC)

The least count is calculated using the difference between the smallest main scale division (MSD) and the smallest vernier scale division (VSD).

1. Main Scale Division (MSD): The main scale is graduated in mm, so:
   1 MSD=1 mm
2. Vernier Scale Division (VSD): It’s given that 10 divisions on the vernier scale (VSD) are equal in length to 9 mm on the main scale (MSD).
   10 VSD=9 MSD
   1 VSD=109​ MSD=0.9 mm
3. Least Count Formula:
   LC=1 MSD−1 VSD
   LC=1 mm−0.9 mm
   LC=0.1 mm

(ii) Zero Error (ZE)

The zero error is determined by the position of the vernier scale zero relative to the main scale zero when the jaws are in contact.

1. Determine the Type of Zero Error:
   • The problem states, “the zero of the vernier scale is ahead of the zero of the main scale.” This means the vernier zero has moved past the main scale zero, indicating a Positive Zero Error (+ZE).
2. Determine the Coinciding Division:
   • The 3rd division of the vernier scale coincides with a main scale division.
   • Coinciding Vernier Scale Division (n) =3
3. Zero Error Formula (for Positive Error):
   ZE=+(n×LC)
   ZE=+(3×0.1 mm)
   ZE=+0.3 mm

Final Answer Summary:

(i) The least count is 0.1 mm.

(ii) The zero error is +0.3 mm.

Question  6. 

The main scale of a vernier caliper is calibrated in mm and 19 divisions of main scale are equal in length to 20 divisions of the vernier scale. In measuring the diameter of a cylinder by this instrument, the main scale reads 35 divisions and the 4th division of vernier scale coincides with a main scale division. Find

(i) Least count and (ii) Radius of a cylinder.

Ans:

Given Data:

• 1 Main Scale Division(MSD)=1 mm (since the main scale is calibrated in mm).
• 20 Vernier Scale Divisions(VSD)=19 MSD.
• Main Scale Reading(MSR)=35 divisions =35.0 mm.
• Vernier Scale Coincidence(VSC)=4.
• Zero error is not mentioned, so it is assumed to be zero.

(i) Least Count (LC)

The least count is the difference between 1 MSD and 1 VSD.

From the relation 20 VSD=19 MSD, we get 1 VSD=2019​ MSD.

LC​=1 MSD−1 VSD=1 MSD−2019​ MSD=201​ MSD​

Since 1 MSD=1 mm:

LC=201​×1 mm=0.05 mm

(ii) Radius of a Cylinder

First, find the Diameter (D) using the formula:

Diameter=MSR+(VSC×LC)

D​=35.0 mm+(4×0.05 mm)=35.0 mm+0.20 mm=35.20 mm​

Next, calculate the Radius (R):

Radius(R)=2Diameter​

R=235.20 mm​=17.60 mm

Question  7.

In the vernier callipers, there are 10 divisions on the vernier scale and 1 cm on the main scale is divided into 10 parts. While measuring the length, the zero of the vernier lies just ahead of the 1.8 cm mark and the 4th division of vernier coincides with a main scale division.

(a) Find the length.

(b) If the zero error of vernier callipers is -0.02 cm, What is the correct length ?

Ans:

# Given values

MSR = 1.8  # Main Scale Reading in cm

VSC = 4    # Vernier Scale Coincidence

MSD = 0.1  # Main Scale Division in cm (1 cm / 10 divisions)

N = 10     # Number of divisions on Vernier Scale

ZE = -0.02 # Zero Error in cm

# 1. Calculate the Least Count (LC)

LC = MSD / N

print(f”Least Count (LC): {LC}”)

# 2. Calculate the Measured Length (L_obs)

L_obs = MSR + (VSC * LC)

print(f”Measured Length (L_obs): {L_obs}”)

# 3. Calculate the Correct Length (L_correct)

L_ Correct = L_obs – ZE

print(f”Correct Length (L_correct): {L_correct}”)

Code output

Least Count (LC): 0.01

Measured Length (L_obs): 1.84

Correct Length (L_correct): 1.86

Question 8.

While measuring the length of a rod with vernier callipers, below shows the position of its scales. What is the length of the rod?

Ans:

To find the length of the rod, you need to calculate the Observed Length using the Main Scale Reading (MSR), Vernier Scale Coincidence (VSC), and Least Count (LC).

1. Determine Instrument Constants

The image shows a standard Vernier Callipers setup. You must first deduce the Least Count (LC).

• Smallest Main Scale Division (MSD): The main scale divisions are typically in millimeters. Assuming a standard scale, the smallest division is 1 mm or 0.1 cm.
• Vernier Scale Divisions (N): The image shows 10 divisions on the Vernier Scale.
• Least Count (LC):
  LC=NSmallest MSD​=100.1 cm​=0.01 cm

2. Record the Readings

• Main Scale Reading (MSR): This is the reading on the main scale just before the zero mark of the Vernier scale.
  • The Vernier zero is past the 3.2 cm mark but hasn’t reached the 3.3 cm mark.
  • MSR=3.2 cm
• Vernier Scale Coincidence (VSC): This is the Vernier scale division that perfectly coincides with any main scale division.
  • Observing the image, the 6th division on the Vernier scale lines up exactly with a main scale division.
  • VSC=6

3. Calculate the Length

The Observed Length (Lobs​) is calculated as:

Lobs​=MSR+(VSC×LC)

Substituting the values:

Lobs​=3.2 cm+(6×0.01 cm)Lobs​=3.2 cm+0.06 cmLobs​=3.26 cm

The length of the rod is 3.26 cm. (This value assumes the Vernier Callipers has no zero error.)

Question  9. 

The pitch of a screw gauge is 0.5 mm and the head scale is divided in 100 parts. What is the least count of a screw gauge?

Ans:

The least count (LC) of a screw gauge is 0.005 mm.

The least count is defined as the pitch (the linear distance moved by the screw for one full rotation) divided by the total number of divisions on the circular scale.

LC=Number of Circular Divisions / Pitch​

Using the provided values:

LC=1000.5 mm​=0.005 mm

Question  10. 

The thimble of a screw gauge has 50 divisions. The spindle advances 1 mm when the screw is turned through two revolutions.

(i) What is the pitch of the screw gauge?

(ii) What is the least count of the screw gauge?

Ans:

The pitch and least count (LC) are fundamental constants of a screw gauge that determine its precision.

Pitch of the Screw Gauge

The pitch is the linear distance the screw’s spindle advances when the thimble completes one full rotation.

• Calculation:
  Pitch=Number of Full Rotations / Distance Advanced​=21 mm​=0.5 mm

Least Count (LC) of the Screw Gauge

The least count is the smallest length the instrument can measure and is calculated by dividing the pitch by the total number of divisions on the thimble.

• Calculation:
  LC=Number of Divisions on Thimble / Pitch​=500.5 mm​=0.01 mm

Question  11. 

The pitch of a screw gauge is 1 mm and the circular scale has 100 divisions. In measurement of the diameter of a wire, the main scale reads 2 mm and 45th mark on the circular scale coincides with the base line. Find

(i) The least count and

(ii) The diameter of the wire.

Ans:

(i) Least Count (LC)

The Least Count of a screw gauge is the ratio of the pitch to the total number of divisions on the circular scale.

LC=Number of Circular Scale Divisions /Pitch​

Given:

• Pitch =1 mm
• Circular Scale Divisions =100

LC=1001 mm​=0.01 mm

(ii) Diameter of the Wire

The total measured reading (diameter) is the sum of the Main Scale Reading and the Circular Scale Reading, assuming there is no zero error (since none was specified).

Diameter=Main Scale Reading (MSR)+(Circular Scale Coincidence (CSC)×LC)

Given:

• MSR=2 mm
• CSC=45th mark
• LC=0.01 mm

Diameter=2 mm+(45×0.01 mm)

Diameter=2 mm+0.45 mm

Diameter=2.45 mm

Question  12. 

When a screw gauge with a least count of 0.01 mm is used to measure the diameter of a wire, the reading on the sleeve is found to be 1 mm and the reading on the thimble is found to be 27 divisions.

(i) What is the diameter of the wire in cm?

(ii) If the zero error is +0.005 cm, what is the correct diameter?

Ans:

The measurement utilized a screw gauge with a Least Count (LC) of 0.01 mm (Sleeve Reading=1 mm and Thimble Reading=27), and the instrument has a Positive Zero Error (ZE) of +0.005 cm.

(i) Observed Diameter of the Wire

The measured length before correction, or Observed Diameter (Dobs​), is calculated by combining the main scale (sleeve) and circular scale (thimble) readings:

Dobs​=Sleeve Reading+(Thimble Reading×LC)

1. Calculation in mm:
   Dobs​=1 mm+(27×0.01 mm)
   Dobs​=1 mm+0.27 mm=1.27 mm
2. Conversion to cm (1 cm=10 mm):
   Dobs​=101.27 mm​=0.127 cm

The observed diameter of the wire is 0.127 cm.

(ii) Correct Diameter of the Wire

To find the true length, the Correct Diameter (Dcorrect​) is determined by algebraically subtracting the Zero Error from the observed reading:

Dcorrect​=Dobs​−Zero Error

Since the zero error is positive (ZE=+0.005 cm), the correction involves subtracting 0.005 cm from the measured value:

Dcorrect​=0.127 cm−(+0.005 cm)

Dcorrect​=0.127 cm−0.005 cm=0.122 cm

The correct diameter of the wire is 0.122 cm.

Question  13. 

A screw gauge has 50 divisions on its circular scale and its screw moves by 1 mm on turning it by two revolutions. When the flat end of the screw is in contact with the stud, the zero of the circular scale lies below the base line and the 4th division of the circular scale is in line with the base line. Find

(i) The pitch,

(ii) The least count and

(iii) The zero error of the screw gauge

Ans:

Given Data

• Number of divisions on circular scale (N) =50
• Distance moved by screw =1 mm for 2 revolutions
• Zero of circular scale is below the base line (indicating Positive Zero Error)
• Coinciding circular scale division (n) =4th

(i) Pitch

The pitch (P) is the distance moved by the screw for one complete revolution.

P=Number of complete rotations / Distance moved by screw​

P=2 revolutions / 1 mm​=0.5 mm

(ii) Least Count

The least count (LC) is the pitch divided by the total number of divisions on the circular scale.

LC=Number of divisions on circular scale / Pitch​

LC=500.5 mm​=0.01 mm

(iii) Zero Error

Since the zero of the circular scale lies below the base line, the instrument has a Positive Zero Error (ZE).

ZE=+(Coinciding Circular Scale Division×LC)

ZE=+(4×0.01 mm)

ZE=+0.04 mm

Question 14. 

Fig., below shows the reading obtained while measuring the diameter of a wire with a screw gauge. The screw advances by 1 division on the main scale when the circular head is rotated once.

Find:

(i) Pitch of the screw gauge,

(ii) Least count of the screw gauge and

(iii) The diameter of the wire.

Ans:

(i) Pitch of the Screw Gauge

The Pitch is the linear distance moved by the screw when the circular scale is rotated by one full rotation.

Given in the question: “The screw advances by 1 division on the main scale when the circular head is rotated once.”

From the main scale in the figure: The smallest division visible is 1 mm.

Pitch=1 Main Scale Division (MSD)=1 mm

(ii) Least Count of the Screw Gauge

The Least Count (LC) is the smallest distance that can be accurately measured by the screw gauge. It is calculated by:

LC=Total number of divisions on the circular scale (CSD)Pitch​

From the figure, the circular scale has 100 divisions (the markings are from 0 to 90 and back to 0, implying 100 divisions in total).

LC=1001 mm​

LC=0.01 mm

(iii) The Diameter of the Wire

The total reading (TR) or diameter is the sum of the Main Scale Reading (MSR) and the Circular Scale Reading (CSR).

TR=MSR+CSR

TR=MSR+(VSC×LC)

1. Main Scale Reading (MSR): The last complete division visible on the main scale before the edge of the circular scale.
   MSR=4 mm
2. Circular Scale Coincidence (VSC): The circular scale division that aligns with the main scale’s reference line (the index line).
   VSC=80
   (The mark is between 80 and 90, exactly at the 80th mark).
3. Circular Scale Reading (CSR):
   CSR=VSC×LC
   CSR=80×0.01 mm=0.80 mm
4. Total Reading (Diameter):
   Diameter=4 mm+0.80 mm
   Diameter=4.80 mm

Question  15.

A screw has a pitch equal to 0.5 mm. What should be the number of divisions on its head so as to read correctly up to 0.001 mm with its help?

Ans:

This is determined using the fundamental relationship between the tool’s precision (Least Count), its thread size (Pitch), and the number of divisions on the rotating scale.

Calculation

The formula linking these values is:

Least Count (LC)= Number of Divisions (N) / Pitch​

To find the required number of divisions (N), we rearrange the formula:

N=Least Count (LC) / Pitch​

Given Values:

• Pitch =0.5 mm
• Required LC=0.001 mm

Substitution:

N=0.001 mm / 0.5 mm​

N=500

Therefore, the circular head must be divided into 500 equal parts to obtain the desired precision.

Exercise 1 (C)

Question  1. 

What is a simple pendulum? Is the pendulum used in a pendulum clock a simple pendulum? Give reason to your answer.

Ans:

A simple pendulum is an idealized model consisting of a point mass (called the bob) suspended by a massless, inextensible string from a fixed support. It is a theoretical construct used to study periodic motion, where the only forces acting are gravity and the tension in the string. The period of oscillation for a simple pendulum depends only on the length of the string and the acceleration due to gravity, provided the angle of swing is small. 

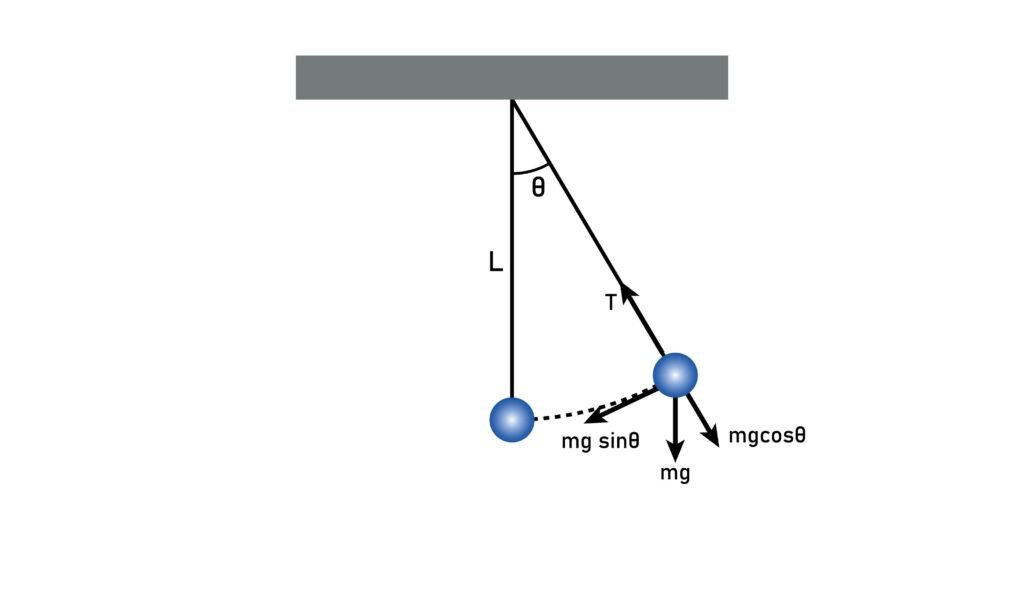
Pendulum Clock and Simple Pendulum

The pendulum used in a pendulum clock is not a simple pendulum; it is a compound pendulum (or physical pendulum).

Reason

• Mass Distribution: A simple pendulum assumes all the mass is concentrated at a single point (the bob), and the rod/string has zero mass. In contrast, the pendulum of a clock has a heavy metal bob suspended by a rod (not a massless string), and the mass of this rod is not negligible.
• Center of Mass: For the simple pendulum model to be strictly accurate, the dimensions of the bob must be much smaller than the length of the string. In a clock pendulum, the mass is distributed throughout the large bob and the rod, meaning the motion is governed by its overall center of mass and moment of inertia, not just the point mass at the end.

Question  2.

(a) Define the terms : oscillation 

(b) Define the term amplitude.

(c) Define the term frequency.

(d) Define the terms : time period as related to a simple pendulum.

Ans:

Here are the definitions of the terms related to a simple pendulum and periodic motion:

(a) Oscillation

An oscillation is a single complete to-and-fro motion of a body from its mean (equilibrium) position, through one extreme position, back through the mean position to the other extreme position, and finally returning to its mean position.

(b) Amplitude

The amplitude (A) is the maximum displacement of an oscillating body (like a pendulum bob) from its mean (equilibrium) position to one of its extreme positions. It is a measure of the energy or intensity of the oscillation.

(c) Frequency

The frequency (f) is the number of complete oscillations (or cycles) performed by an oscillating body per unit of time (usually per second).

• Its SI unit is the hertz (Hz), where 1 Hz=1 oscillation per second.

(d) Time Period

The time period (T), as related to a simple pendulum, is the time taken by the pendulum to complete one full oscillation (one to-and-fro movement).

• It is the reciprocal of frequency: T=1/f.
• Its SI unit is the second (s).

Question  3. 

Draw a neat diagram of a simple pendulum. Show on it the effective length of the pendulum and its one oscillation .

Ans:

Here is a neat diagram of a simple pendulum, illustrating its effective length and one complete oscillation.

---

Key Components Illustrated:

• Fixed Support: The point from which the pendulum is suspended.
• Massless, Inextensible String: The ideal string that does not stretch and has negligible mass.
• Point Mass Bob (M): The idealized mass concentrated at a single point at the end of the string.
• Effective Length (L): This is the crucial measurement for a simple pendulum. It is the distance measured from the point of suspension to the center of gravity of the bob.
• Mean Position (Equilibrium Position): The central position where the bob rests when not oscillating.
• Extreme Positions (A and B): The maximum displacement positions on either side of the mean position.

One Complete Oscillation:

An arrowed path demonstrates one complete oscillation of the pendulum. This is defined as the bob starting from one extreme position (e.g., A), moving through the mean position to the other extreme position (B), and then returning back to the initial extreme position (A).

A→Mean Position→B→Mean Position→A

Alternatively, it can be defined as moving from the mean position to one extreme, then to the other extreme, and back to the mean position.

Mean Position→A→Mean Position→B→Mean Position

The diagram also indicates that the angle of swing (δ) is small, which is a condition for the pendulum’s motion to be considered simple harmonic.

Question  4.

Name two factors on which the time period of a simple pendulum depends. Write the relation for the time period in terms of the above named factors.

Ans:

The period of oscillation for an ideal simple pendulum is governed by two key parameters: its length and the local gravitational acceleration.

Governing Factors

1. Pendulum Length (L):
   • This is the distance measured from the pivot point (suspension) to the central point of the bob’s mass.
   • Relation: The time period (T) is directly proportional to the square root of the length (T∝L). This means a longer pendulum takes more time to complete one swing. 
2. Acceleration due to Gravity (g):
   • This represents the strength of the gravitational field where the pendulum is located.
   • Relation: The time period (T) is inversely proportional to the square root of gravity (T∝1/g). If gravity is stronger, the restoring force is greater, and the pendulum swings back faster, resulting in a shorter period.

Time Period Formula

The precise mathematical relationship for the time period (T) under the condition of small angle swings is:

T=2πgL​

This formula shows that the period is independent of the bob’s mass and the amplitude of the swing (provided the amplitude is small).

Question  5. 

Name two factors on which the time period of a simple pendulum does not depend.

Ans:

The time period of a simple pendulum does not depend on two main factors:

1. Mass of the bob: The period is the same whether the suspended mass is large or small.
2. Amplitude of the swing: Provided the angle of swing is small (usually less than 10∘ to 15∘), the time period is independent of how far the bob swings.

Question  6. 

How is the time period of a simple pendulum affected, if at all, in the following situations:

The length is made four times.

The acceleration due to gravity is reduced to one-fourth.

Ans:

Question  7.

How are the time period T and frequency f of an oscillation of a simple pendulum related ?

Ans:

The time period (T) and the frequency (f) of a simple pendulum’s oscillation have a reciprocal relationship. They are inversely proportional.

Defining the Relationship

The relationship means that one is the inverse of the other:

T=1 / f

and

f=1 / T

Key Terms

• Time Period (T): The duration (in seconds) required for the pendulum to complete one cycle (one full back-and-forth swing).
• Frequency (f): The rate at which oscillations occur, defined as the number of cycles completed in one second (measured in Hertz, Hz, or s−1).

Question  8. 

How do you measure the time period of a given pendulum? Why do you note the time for more than one oscillation?

Ans:

It’s found by timing many swings and calculating the average time per swing.

Measuring the Time Period

1. Set Up: Suspend the pendulum bob and gently release it from a small angle (amplitude).
2. Timing: Start a stopwatch precisely as the bob passes a fixed reference point (like the center or an end point).
3. Count: Count the number of full oscillations, n (usually 20 to 50).
4. Record: Stop the stopwatch exactly when the n-th oscillation is completed and record the total time, t.
5. Calculate: Determine the period using the formula:
   T=nt​

Why Use Multiple Oscillations?

The time is noted for multiple oscillations to reduce human error and increase the accuracy of the measurement.

• Error Distribution: Human reaction time introduces slight errors when starting and stopping the stopwatch (δt). By measuring the time for 20 swings, this error is spread out, making the error in the final period δT=20δt​, significantly smaller.
• Precision: Since the period is typically short (e.g., 2 s), measuring a longer total time (e.g., 40 s) ensures that the recorded time spans a larger interval, allowing the resolution of the stopwatch to provide a more reliable average value for a single period.

Question  9. 

How does the time period (T) of a simple pendulum depend on its length (l)? Draw a graph showing the variation of T2 with l. How will you use this graph to determine the value of g (acceleration due to gravity)?

Ans:

The time period (T) of a simple pendulum is directly proportional to the square root of its length (l), provided the angular displacement is small.

T∝l

The mathematical relationship is given by the formula:

T=2πgl​

Graph: Variation of T2 with l

To obtain a linear relationship suitable for graphing, we square the time period formula:

T2=4π2(gl​)

This equation is in the linear form y=mx, where:

• y=T2
• x=l
• m=g4π2​ (The slope)

A graph plotting T2 on the y-axis against l on the x-axis will be a straight line passing through the origin, with a positive slope.

Determining the Value of g

The value of the acceleration due to gravity (g) can be determined from the slope (m) of the T2 vs. l graph.

1. Calculate the Slope (m): Choose two distinct points (l2​,T22​) and (l1​,T12​) on the straight line and calculate the slope:
   m=Slope=l2​−l1​T22​−T12​​
2. Relate Slope to g: Since the theoretical slope is m=g4π2​, we can rearrange this equation to solve for g:
   g=Slope4π2​

By substituting the experimentally determined slope into this equation, the local value of the acceleration due to gravity can be accurately calculated.

Question  10. 

Two simple pendulums A and B have equal lengths, but their bobs weigh 50 gf and 100 gf, respectively. What would be the ratio of their time periods? Give reasons for your answer.

Ans:

The ratio of the time periods of pendulum A to pendulum B will be 1:1. The time period of a simple pendulum is independent of the mass (or weight) of its bob. The formula for the time period (T) is T=2πgL​​, which depends only on the length (L) and the acceleration due to gravity (g). Since both pendulums A and B have equal lengths and are subject to the same acceleration due to gravity (assuming they are in the same location), their time periods must be equal, regardless of the difference in their bob’s weight (50 gf vs 100 gf). Thus, the ratio TA​:TB​ is 1:1.

Question  11. 

Two simple pendulums A and B have lengths 1.0 m and 4.0 m, respectively, at a certain place. Which pendulum will make more oscillations in 1 min? Explain your answer.

Ans:

The relationship between the time period (T) and the length (L) of a simple pendulum is T∝L​. Since frequency (f) is the reciprocal of the period (f=1/T), the frequency is inversely proportional to the square root of the length (f∝1/L​). Pendulum A (length 1.0 m) will make more oscillations in 1 minute than Pendulum B (length 4.0 m). Because Pendulum A is four times shorter than Pendulum B in length, its period will be 4​=2 times shorter, and therefore its frequency will be 2 times greater. Since frequency is the number of oscillations per second, the pendulum with the greater frequency (Pendulum A) will complete more oscillations in the given time frame of one minute.

Question 12. 

State how does the time period of a simple pendulum depends on 

(a) length of pendulum, 

(b) mass of bob, 

(c) amplitude of oscillation and 

(d) acceleration due to gravity.

Ans:

Factor	Dependence of Time Period (T)	Explanation
(a) Length (L)	Directly proportional to the square root of the length (T∝L​).	A longer pendulum has a longer period and swings slower.
(b) Mass of Bob (m)	Independent.	Changing the mass of the bob does not change the time period (assuming the bob is a point mass and the rod is massless).
(c) Amplitude (a)	Independent (for small angles).	As long as the initial angle is small (less than about 10∘), the period remains constant.
(d) Acceleration due to Gravity (g)	Inversely proportional to the square root of gravity (T∝1/g​).	Where gravity is stronger (larger g), the period is shorter, and the pendulum swings faster.

Question  13. 

What is a second’s pendulum?

Ans:

A second’s pendulum is simply a specialized simple pendulum with a precisely defined time period (T) of exactly two seconds. This means it takes one full second for the pendulum bob to complete a half-swing, traveling from one extreme end of its arc to the opposite extreme end, and another second to make the return swing, resulting in one complete oscillation every two seconds. This specific period makes it historically useful for basic timekeeping. 

Question  14. 

State the numerical value of the frequency of oscillation of a second’s pendulum. Does it depend on the amplitude of oscillations?

Ans:

The frequency of oscillation for a second’s pendulum is 0.5 Hz (or 0.5 oscillations per second), because its time period (T) is, by definition, exactly 2 seconds (T=1/f). The frequency does not depend on the amplitude of the oscillations, provided the pendulum swings with a small amplitude (typically less than 10∘ or 15∘), as its motion approximates simple harmonic motion under that condition.

Exercise 1 (C)

Question 1.

If the length of a simple pendulum is made one-fourth, then its time period becomes

1. Four times
2. One-fourth
3. Double
4. Half

Question  2.

The time period of a pendulum clock is : 

1. 1 s
2. 2 s
3. 1 min
4. 12 h

Question  3.

The length of a second’s pendulum is nearly : 

1. 0.5 m
2. 9.8 m
3. 1.0 m
4. 2.0 m

Exercise 1 (C)

Question 1. 

A simple pendulum completes 40 oscillations in one minute. 

Find its

(a) Frequency and (b) Time period.

Ans:

This seems to be the output of a calculation based on an implied scenario. Assuming the context is a simple pendulum experiment where a total of 40 oscillations (n) were timed over a Total Time of 60 seconds (t), here is the concise result and calculation:

(a) Frequency (f)

Frequency is the number of oscillations per unit of time.

f=Total Time (t) / Number of Oscillations (n)​

f=60 s / 40​= 3 / 2​ Hz

f≈0.67 Hz

(b) Time Period (T)

The Time Period is the time taken for one oscillation and is the reciprocal of the frequency.

T=Number of Oscillations (n) / Total Time (t)​=f1​

T=40 / 60 s​=2 / 3​ s

T=1.5 s

Question 2. 

The time period of a simple pendulum is 2 s. What is its frequency? What name is given to such a pendulum? 

Ans:

A pendulum with a time period (T) of 2 s is termed a Seconds Pendulum. This name is derived from the fact that it requires exactly one second to swing from one extreme point to the other (a half-oscillation), completing the full back-and-forth cycle in two seconds. The frequency (f) of this pendulum is the reciprocal of its time period, following the relation f=1/T. By calculation, a 2 s period yields a frequency of 0.5 Hz (1/2 s=0.5 Hz), meaning the device completes half an oscillation every second.

Question 3. 

A second pendulum is taken to a place where acceleration due to the gravity falls to one-fourth. How is the time period of the pendulum affected, if at all? Give reasons. What will be its new time period?

Ans:

Question 4. 

Find the length of a second’s pendulum at a place where g = 10 m s-2 (Take π = 3.14)

Ans:

Question 5. 

Compare the time periods of the two pendulums of lengths 1 m and 9 m.

Ans:

Question 6.

A pendulum completes 2 oscillations in 5 s. What is its time period? If g = 9.8 m s-2, find its length.

Ans:

Question 7. 

The time periods of two simple pendulums at a place are in the ratio 2:1. What will be the corresponding ratio of their lengths?

Ans:

Question 8.

It takes 0.2 s for a pendulum bob to move from the mean position to one end. What is the time period of the pendulum?

Ans:

The time taken for a pendulum bob to move from its mean position to one extreme end is exactly one-quarter (1 / 4​) of its total time period (T).

Given the time for this 1/ 4 oscillation is 0.2 s, the full time period is calculated by multiplying this duration by four:

Time Period (T)=4×(Time for mean to extreme)

T=4×0.2 s

T=0.8 s

The time period of the pendulum is 0.8 seconds.

Question 9. 

How much time does the bob of a second’s pendulum take to move from one extreme of its oscillation to the other extreme?

Ans:

The bob of a seconds pendulum takes 1.0 second to move from one extreme of its oscillation to the other extreme.

Explanation

A seconds pendulum is defined as a simple pendulum whose time period (T) is exactly 2 s. The time period is the time required for one full, complete oscillation.

A complete oscillation involves four quarter-swings:

1. One extreme to the mean position.
2. Mean position to the opposite extreme.
3. Opposite extreme back to the mean position.
4. Mean position back to the starting extreme.

The time taken to move between the two extreme positions (from one end to the other) is exactly half (21​) of the total time period.