Pressure in Fluids and Atmospheric Pressure

This chapter reveals that fluids—both liquids and gases—exert pressure in all directions, a force that is both invisible and powerful. The pressure within a liquid is not uniform; it increases significantly with depth. This is because the weight of the liquid above pushes down on the layers below. A liquid at a greater depth must support more weight, resulting in higher pressure. This principle explains why dams are built with thicker walls at the bottom and why a person feels more pressure in their ears when diving deep underwater. Furthermore, this liquid pressure depends only on the height of the liquid column and its density, not on the shape or surface area of the container. This is why water seeks its own level, and it forms the basis for the interconnected vessels principle.

The transmission of this pressure leads to a crucial application: Pascal’s Law. This law states that a change in pressure applied to an enclosed fluid is transmitted undiminished to every portion of the fluid and the walls of the container. We harness this principle in hydraulic machines like lifts and brakes. By applying a small force to a small-area piston, we create a pressure that is transmitted to a larger-area piston, which then generates a massive output force. This allows us to multiply force dramatically, making it possible to lift heavy cars in a garage with minimal effort.

Shifting from liquids to gases, the chapter explores atmospheric pressure. Our atmosphere is a vast ocean of air, and its weight creates a pressing force on everything at the Earth’s surface. This is demonstrated by classic experiments, such as the mercury barometer invented by Torricelli, which measures this pressure. We don’t feel this colossal force because the pressure inside our bodies balances it. This atmospheric pressure is utilized in everyday tools like drinking straws and syringes; when we suck out the air, the outside atmospheric pressure pushes the liquid up to fill the vacuum. The chapter also explains that this air pressure decreases as we ascend to higher altitudes, as there is less air above us pushing down, which is why aircraft cabins must be pressurized.

Exercise 4 (A)

Question  1. 

Define the term thrust. State its S.I. unit.

Ans:

Thrust is a mechanical force that describes a powerful, directed push. It is the reaction force exerted by an object when it expels mass at high speed, propelling itself in the opposite direction.

In simpler terms, thrust is the driving push that moves a vehicle like a rocket or a jet plane forward. It is generated according to Newton’s third law; as the engine forces exhaust gases backward, the gases push the engine (and the vehicle attached to it) forward with an equal force. This forward force is thrust.

The S.I. unit of thrust is the newton (N). Since thrust is a type of force, it is measured in newtons, which is defined as the force needed to accelerate a one-kilogram mass at a rate of one meter per second squared (1 N = 1 kg·m/s²).

Question  2. 

What is meant by pressure? State its S.I. unit.

Ans:

Pressure describes how concentrated a force is over a specific area. It’s the measure of how much push or squeeze is being applied onto a surface.

Think of it this way: the same total force can feel very different depending on how much space it’s spread over. For instance, the force of your body weight is the same whether you stand on the ground in flat shoes or in high heels. But in high heels, that same force is concentrated into a much smaller area, resulting in a much higher pressure—which is why the heels sink into soft ground more easily.

In scientific terms, pressure is calculated as the amount of force acting perpendicularly on a surface, divided by the area of that surface.

Its S.I. unit is the pascal (Pa). One pascal is defined as a force of one newton pushing on an area of one square metre.

1 pascal (Pa)=1 newton per square metre (N/m²)

Question  3. 

(a) What physical quantity is measured in bar?

 (b) How is the unit bar related to the S.I. unit pascal?

Ans:

(a) Physical Quantity Measured in Bar

The unit bar is used to measure pressure.

Pressure, in simple terms, is the amount of force applied over a specific area. You encounter it in everyday life, such as when checking the air pressure in a car tire or hearing a weather report about atmospheric pressure.

(b) Relationship Between Bar and Pascal

The relationship between the bar and the pascal is direct and fixed:

1 bar is exactly equal to 100,000 pascals.

We can express this as:
1 bar = 10⁵ Pa

This shows that the bar is a much larger unit than the pascal. One pascal is a very small amount of pressure, so using the bar (or the kilopascal, kPa) is often more practical for measuring common pressures like tire inflation or atmospheric conditions. For example, standard atmospheric pressure is about 1.013 bar, which is a much more convenient number than 101,300 pascals.

Question  4. 

Define one pascal (Pa), the S.I. unit of pressure.

Ans:

Think of pressure as a measure of how concentrated a force is over a certain area.

With that in mind, we define the pascal (Pa) by building it from its fundamental units. It is the pressure that results when a force of one newton is spread evenly over a surface area of exactly one square meter.

Since a newton is a relatively small unit of force (roughly the weight of a small apple), and a square meter is a sizable area, one pascal represents a very gentle, barely noticeable pressure. It is the gentle, distributed push you would feel if that single apple were laid flat across the surface of a large coffee table.

In its simplest terms: One pascal is one newton per square meter.

Question  5. 

State whether thrust is a scalar or vector?

Ans:

Thrust is a vector quantity.

The reason for this is that thrust is not just about an amount; it is a force that acts in a specific direction.

To understand why:

• A scalar quantity is defined only by its magnitude (size or amount). Examples include mass, time, and temperature. Saying “the engine produces 50,000 Newtons of thrust” gives the magnitude.
• A vector quantity must be fully described by both magnitude and a direction. To completely describe thrust, you must state both its amount and the direction it is applied. For example, “the rocket engines produce 50,000 Newtons of thrust directed downward to lift the spacecraft upward.”

Question 6.

State whether pressure is a scalar or vector?

Ans:

Pressure is classified as a scalar quantity.

The reason for this lies in its definition. Pressure is defined as the magnitude of the force component acting perpendicularly (normal) on a surface, divided by the area of that surface.

While force is a vector (having both magnitude and direction), pressure itself does not have a specific directional property associated with its nature. It simply transmits its magnitude equally in all directions at a point within a fluid at rest.

Think of it this way: when you inflate a balloon, the air pressure inside pushes outward against the inner walls equally in every direction. It does not push only left or only down. This isotropic (same in all directions) behavior is a definitive characteristic of a scalar quantity. It possesses magnitude but no single, defined direction.

Question 7. 

Differentiate between thrust and pressure.

Ans: 

Feature	Thrust	Pressure
Definition	The force acting perpendicularly (normal) to a surface.	The thrust or force acting per unit area of a surface.
Formula	Thrust = Force (F)	Pressure = Area / Thrust​ or P=A /F​
Nature	Vector quantity (has both magnitude and direction).	Scalar quantity (has only magnitude).
SI Unit	Newton (N), as it is a force.	Pascal (Pa) or N/m2.
Effect	The total force exerted on the surface.	The effect or intensity of the force on a unit area. A small area results in high pressure for the same thrust.
Examples	The upward force exerted by a fluid on a submerged object (Upthrust/Buoyant force); the force that propels a rocket or jet engine.	The force on the blade of a sharp knife (small area = high pressure); atmospheric pressure; the pressure inside an inflated balloon.

Question 8. 

How does the pressure exerted by thrust depend on the area of surface on which it acts? Explain with a suitable example.

Ans:

The pressure exerted by a thrust depends inversely on the area of the surface on which it acts. This means that for a constant thrust, a smaller contact area results in significantly higher pressure, while a larger contact area results in much lower pressure.

This relationship is best understood through the formula:
Pressure = Thrust / Area

You can see that pressure and area are on opposite sides of the fraction. If the Area in the denominator gets smaller, the overall value of Pressure gets larger, provided the Thrust (the force applied perpendicularly) remains the same.

A Concrete Example: The Knife’s Edge

Consider the simple action of cutting a vegetable.

A sharp knife has a blade that tapers to a very fine edge. This means the cutting edge has an extremely small surface area. When you apply a downward thrust (force) with the knife, all of that force is concentrated onto that tiny edge. The resulting pressure becomes immense—so high that it easily overcomes the strength of the vegetable’s fibers, allowing the blade to slice through cleanly.

Now, imagine trying to cut the same vegetable with a dull knife. A dull knife has a wider, rounded edge, meaning it has a much larger surface area in contact with the vegetable. If you apply the same amount of thrust as you did with the sharp knife, this force is now spread out over this larger area. The resulting pressure is therefore much lower. It is insufficient to sever the fibers effectively, and the knife will tend to crush or bruise the vegetable rather than cutting it smoothly.

Thus, the same thrust produces a world of difference in outcome solely because of the surface area it acts upon. This inverse relationship is why all cutting and piercing tools—from needles and nails to axes and spears—are designed with a sharp point or edge.

Question 9. 

Why is the tip of an allpin made sharp?

Ans:

The sharp tip of a pin is a brilliant exploitation of a simple principle of physics: concentrating force to overcome resistance.

Think of the difference between trying to push a blunt thumbtack into a corkboard and a sharp one. The blunt one will press against a wide area of the cork’s surface, and the cork fibers, sharing the push among themselves, resist easily. The sharp pin, however, is a trick of geometry. It gathers the entire pushing force from your hand and focuses it onto a single, minuscule point at its tip.

This incredible concentration of energy is like the difference between pressing a block of wood against your skin and pressing a needle. The block spreads the force harmlessly, while the needle’s point applies the same total force to such a tiny area that it effortlessly pierces the surface.

For a pin, this means it can part the woven threads of fabric or push aside the particles of a wall with minimal effort from the user. The sharpness ensures that all the energy from your push is used not to just press broadly, but to cut and separate at a microscopic level, allowing the pin to slide in smoothly and hold its place.

Question 10. 

(a) Explain the following statement: It is easier to cut with a sharp knife than with a blunt one.

(b) Explain the following statement:Sleepers are laid below the rails.

Ans:

(a) 

This difference comes down to how force is concentrated. When you push down on a knife, you apply a certain amount of force.

A sharp knife has a very fine edge, meaning the blade tapers down to an extremely thin line. This tiny edge is the only part that makes contact with the object you’re cutting. As a result, all the downward force from your hand is focused onto a miniscule area. This intense concentration of force creates immense pressure at the point of contact, allowing the blade to pierce and separate the material with ease.

A blunt knife, in contrast, has a wider, rounded edge. The same amount of force from your hand is now spread out over a much larger surface area. This drastically reduces the pressure exerted on the material. Instead of slicing through cleanly, the blade tends to crush and tear its way through, requiring significantly more effort.

Think of it like the difference between pressing a pin and a bottle cap into your skin with the same force. The pin’s point concentrates the force to create high pressure and pierces easily, while the bottle cap spreads the force out, creating low pressure and causing no puncture.

(b) Sleepers are laid below the rails.

Sleepers (or railroad ties) are the horizontal slabs of wood or concrete placed underneath and across the steel rails. Their primary job is to distribute weight and prevent sinking.

A train is an immensely heavy object. Without sleepers, the narrow steel rails would bear the entire weight of the passing train, concentrating it on two very thin lines. On soft ground like soil or gravel, this enormous pressure would cause the rails to sink, bend, and become misaligned, making the track unstable and dangerous.

The sleepers solve this by acting as a stable, wide foundation. They lie perpendicular to the rails, effectively “catching” the load from the rails and spreading it out over a much wider area of the ground beneath. This distribution dramatically reduces the pressure on the ground, preventing the rails from sinking and ensuring the track remains level, secure, and able to handle the train’s weight safely.

In essence, sleepers function like snowshoes for a train track. Just as snowshoes stop a person from sinking into soft snow by spreading their weight, sleepers stop the rails from sinking into the ground by spreading the train’s weight.

Question 11. 

What is a fluid?

Ans:

A fluid is a substance that cannot resist a changing shape when it is met with a force. Its primary nature is to yield and to flow. This category of matter includes both liquids and gases.

What truly defines a fluid is the relationship between its molecules and how they respond to pressure. Unlike in a solid, where molecules are locked in a fixed structure, the molecules in a fluid are mobile. They can slide past one another with relative freedom.

When you apply a push or a shear force to a fluid, it does not develop a permanent resistance. Instead, it contorts and moves, continuously deforming for as long as the force is applied. A liquid, like water, will flow to fill the bottom of a container, adopting its shape while retaining a nearly fixed volume. A gas, like air, will expand to fill every available space, its volume changing readily.

In essence, a fluid is any substance that offers no lasting opposition to a change in its form. It is defined by its readiness to travel, to adapt, and to be reshaped by the slightest imbalance in force, making all liquids and gases kin in their behavior.

Question 12. 

What do you mean by the term fluid pressure?

Ans:

Think of fluid pressure as a hidden, constant push that a fluid—which can be either a liquid or a gas—exerts on every single surface it touches. It is a silent force that acts in all directions at once.

This pressure originates from the countless, tiny particles that make up the fluid. These particles are never still; they are in a state of continuous, frantic motion. In a liquid, they slide and jostle past one another. In a gas, they fly around at high speeds.

As these particles move, they constantly collide with each other and with any object placed within the fluid. Each collision delivers a tiny, individual push. Fluid pressure is the combined effect of a vast number of these microscopic collisions happening every second. It is the total force of all these tiny pushes spread over a specific area.

A key feature of this pressure is that it pushes equally in all directions at a given point. If you submerge your hand in water, you feel this push against your palm, the back of your hand, and your fingers simultaneously. It’s not a one-directional force like wind; it is a truly surrounding squeeze.

The strength of this push isn’t constant everywhere. It increases with depth. The deeper you go into a fluid, the greater the weight of the fluid above you, and the more intensely the particles are squeezed together, leading to more forceful collisions. This is why a scuba diver feels the increasing squeeze on their eardrums as they descend, or why a dam must be much thicker at its base than at the top to withstand the greater push from the deep water.

Question 13. 

How does the pressure exerted by a solid and fluid differ?

Ans:

The way a solid and a fluid exert pressure stems from a fundamental difference in their physical structure, leading to two distinct behaviors.

A solid exerts pressure in a defined, directional manner. Because a solid has a rigid structure, any force applied to it is transmitted in a specific direction. For instance, the pointed heel of a shoe applies pressure straight down onto a floor. The force is confined to the area of contact and points in the direction it was pushed. The pressure exists only where the solid makes contact and is directed along the line of the applied force.

A fluid (which includes both liquids and gases), in contrast, exerts pressure in all directions at any given point. This is because the molecules in a fluid are not locked in place but move freely. When a force is applied, it is transmitted equally in all directions by these mobile particles. When you are submerged in water, you feel the water’s push against your front, back, sides, and everywhere on your body simultaneously. This pressure isn’t just downward; it’s omnidirectional. Furthermore, fluid pressure increases with depth, as the weight of the fluid above creates a greater force, which is then transmitted in all directions.

In essence, the key difference is this: A solid presses down along a specific path, while a fluid presses inward from all sides at once. A solid’s pressure is directional and localized, but a fluid’s pressure is encompassing and pervasive.

Question 14.

Describe a simple experiment to demonstrate that a liquid enclosed in a vessel exerts pressure in all directions.

Ans:

The Balloon and Water Fountain Experiment

This experiment visually shows water being forced out from all sides of a flexible container, proving the liquid’s internal pressure is omnidirectional.

You will need:

1. A large, sturdy, transparent plastic bag (like a freezer bag).
2. Water.
3. A few rubber bands.
4. A sharp pushpin or thumbtack.
5. A tray or a basin to catch water.

A helper (optional but useful).

Procedure:

1. Prepare the “Vessel”: Take the plastic bag and fill it about three-quarters full with water. Seal the top of the bag tightly, squeezing out the excess air, and secure it with a rubber band to prevent any leaks.
2. Create the “Walls”: Your sealed, water-filled bag now represents the enclosed vessel.
3. Demonstrate the Pressure:
   • Hold the bag upright over the tray. With your other hand, quickly and carefully poke a hole in the front of the bag with the pushpin. Observe a stream of water jetting out forwards.
   • Now, while the first hole is still leaking, poke a second hole in the top of the bag. You will immediately see a new stream of water shooting upwards.
   • Next, poke a hole in one side of the bag. A stream will jet out sideways.
   • Finally, poke a hole in the bottom. A strong stream will flow downwards.

Observation:

You will see distinct jets of water spurting out from every single hole you create, regardless of its position—top, bottom, front, back, or sides. The water is not just falling out due to gravity; it is being actively pushed out by the pressure within the bag. The upward jet from the top hole is the most conclusive, as it proves the pressure is not just downward (from gravity) but acts forcefully in all directions, even against gravity.

Conclusion:

The water inside the sealed bag exerts a force perpendicular to the inner surface of the bag at every point. Because the bag is flexible, this force results in water being ejected from any opening made in the container. The fact that jets appear from holes in the top, sides, and bottom simultaneously proves that the enclosed liquid exerts pressure in all directions equally.

Question 15.

State three factors on which the pressure at a point in a liquid depends.

Ans:

The pressure experienced at any specific location within a liquid, like water in a tank or the ocean, is determined by three key elements:

1. The Vertical Height of Liquid Above: The most direct influence is the depth of the point itself. The deeper you go, the greater the weight of the liquid column pressing down from above. A point at the bottom of a deep swimming pool feels far more pressure than a point just below the surface, because it supports a much taller column of water.
2. The Density of the Liquid: The substance of the liquid itself is crucial. A denser liquid, like seawater, has more mass packed into the same volume compared to a lighter liquid like freshwater. This means that at an identical depth, the heavier liquid will exert a stronger push because the column of liquid above the point simply weighs more.
3. The Local Strength of Gravity: The force that gives the liquid its weight is gravity. The pressure we calculate is directly dependent on the value of gravitational acceleration (g). If you could take a container of water to the Moon, where gravity is weaker, the pressure at the bottom would be significantly less because the liquid column would be lighter. On a larger planet with stronger gravity, the same depth would produce a much higher pressure.

Question 16. 

Write an expression for the pressure at a point inside a liquid. Explain the meaning of the symbols used.

Ans:

The pressure at a specific point submerged in a liquid is given by the expression:

P = P₀ + ρgh

Here is the meaning of each symbol in this relationship:

• P: This represents the total pressure at the point inside the liquid. It is the combined force per unit area experienced at that exact location, measured in pascals (Pa).
• P₀: This is the external pressure applied at the liquid’s surface. Most commonly, this is the atmospheric pressure pushing down on the liquid from above. However, it could be any pressure, such as that from a piston in a closed container.
• ρ (the Greek letter ‘rho’): This symbolizes the density of the liquid. It tells us how much mass of the liquid is packed into a given volume. A denser liquid, like mercury, will create a greater increase in pressure with depth than a less dense one, like water.
• g: This is the acceleration due to gravity. Its constant pull downward is what gives the weight to the column of liquid above the point, and is thus fundamental to the pressure we calculate.
• h: This denotes the vertical depth of the point from the liquid’s surface. It is not the length of the container, but the straight-down distance from the surface to the point in question. The pressure increases linearly as you go deeper.

In essence, the formula P = P₀ + ρgh tells us that the total pressure at a point is the sum of the pressure already on the liquid’s surface plus the pressure exerted by the weight of the liquid column directly above that point.

Question 17. 

Deduce an expression for the pressure at depth inside a liquid.

Ans:

Imagine a point submerged deep within a stationary liquid. To find the pressure at this point, we don’t just consider the liquid directly above it; we must account for the entire column of fluid pressing down from the surface.

Let’s visualize a cylindrical column of the liquid with a flat top and bottom, both of area A. The top of this cylinder is right at the free surface of the liquid, open to the atmosphere. The bottom is at the depth *h* where we want to find the pressure.

This column of liquid is at rest. Therefore, all the forces acting upon it must be in equilibrium.

Three primary vertical forces act on our imaginary cylinder:

1. Atmospheric Force, F₁: At the top surface, the atmosphere is pressing down. This force is the atmospheric pressure (P₀) multiplied by the area:
   • F₁ = P₀ A
2. Weight of the Liquid, W: The cylinder itself has weight. Its volume is the area of the base multiplied by the height (A × h). If the liquid has a density ρ, then its mass is ρ × (A h). Therefore, its weight is:
   • W = ρ (A h) g
3. Upward Force from the Liquid Below, F₂: The liquid beneath the cylinder must push upward to support the weight of the cylinder and the force from the atmosphere above it. This upward push is the pressure (P) at depth *h* multiplied by the area of the base. This is the force we are ultimately solving for:
   • F₂ = P A

Since the fluid is in equilibrium, the upward force must perfectly balance the sum of the two downward forces.

Balancing the Forces:
F₂ = F₁ + W

Substituting the expressions we have:
P A = (P₀ A) + (ρ A h g)

Notice that the cross-sectional area A is a common factor in every term. We can divide the entire equation by A to eliminate it, which is a powerful simplification showing that the pressure is independent of the shape or area we imagine.

This leaves us with the fundamental expression for pressure at depth in a liquid:

P = P₀ + ρ g h

Where:

• P is the total pressure at the depth *h*.
• P₀ is the pressure at the liquid’s surface (usually atmospheric pressure).
• ρ is the density of the liquid.
• g is the acceleration due to gravity.
• h is the vertical depth from the surface.

This result shows that the pressure increases linearly with depth, driven directly by the weight of the fluid column above it, and is always greater than the surface pressure P₀.

Question 18. 

How does the pressure at a certain depth in sea water differ from that at the same depth in river water? Explain your answer.

Ans:

The pressure at a specific depth is fundamentally the weight of the water column above that point pressing down. While the depth is identical in both the sea and the river, the key difference lies in the nature of that water column.

Seawater is not pure water; it has a significant amount of salts and minerals dissolved in it. This makes it denser and heavier for a given volume. Imagine two identical columns, one filled with seawater and the other with fresh river water. The column of seawater would simply weigh more.

This difference in weight is what creates the difference in pressure. At the same depth, you are supporting a taller, heavier stack of water in the ocean than you are in the river. The seawater is essentially a heavier fluid, and so it presses down with greater force at every level.

You can think of it like the difference between standing under a tall column of light foam versus a tall column of heavy mud. Even if the columns are the same height, the mud, being denser, would push down on you with much greater force. Similarly, the denser seawater exerts a stronger push, or higher pressure, than river water at the same depth.

Question 19. 

Pressure at the free surface of a water lake is P1, while at a point at depth h below its free surface is P2. (a) How are P1 and P2 related? (b)Which is more P1 or P2?

Ans:

(a) The relationship between the pressure at the free surface (P1) and the pressure at a depth h (P2) is direct and additive. The pressure P2 is equal to the surface pressure P1 plus the pressure exerted by the weight of the water column above that point. This is mathematically expressed as:

P₂ = P₁ + ρgh

where:

• ρ is the density of water,
• g is the acceleration due to gravity, and

(b) Based on the relationship above, P₂ is greater than P₁. This is because P₂ includes the surface pressure P1 and the additional pressure from the water above it (ρgh), which is always a positive quantity. The deeper you go, the more water lies above, and thus the greater the pressure.

Question 20. 

Explain why a gas bubble released at the bottom of a lake grows in size as it rises to the surface of the lake.

Ans:

Imagine you are at the bottom of a deep lake. The weight of all the water above you is pressing down, creating immense pressure. This pressure acts like an invisible, squeezing force on everything at that depth, including a tiny gas bubble just released from the lake bed.

This bubble is mostly empty space filled with air. The high pressure at the bottom forcefully compresses this air, packing the gas molecules tightly together and making the bubble start small.

As the bubble begins its journey upwards, it moves through layers of water that have less and less water above them. With each foot it rises, the weight of the water pressing down from above decreases. This means the squeezing pressure surrounding the bubble is steadily weakening.

The gas molecules inside the bubble have a natural tendency to move apart and fill the space available. They were previously held in a cramped state by the strong external pressure. As this external “squeeze” relaxes during the ascent, the trapped air can finally expand. The energized gas molecules push outward against the now-weaker water pressure, forcing the bubble’s flexible skin to stretch and its volume to increase.

In essence, the bubble grows because the confining force that kept it small is being steadily lifted on the way up. The rising bubble is like a compressed spring that is gradually released; the energy was always there, waiting for the pressure to drop so it could expand and claim more space.

Question  21. 

A dam has broader walls at the bottom than at the top. Explain.

Ans:

A dam is built with thick, sprawling walls at its base and a narrower top because it must hold back an immense, heavy substance that pushes sideways with far greater force at the lowest depths.

Think of the body of water behind the dam not as a single, solid mass, but as a stack of individual layers. The weight of all the water from the surface down to the bottom accumulates, pressing down. This vertical weight translates into a horizontal push against the dam wall.

This sideways pressure is not the same at every depth. The water at the very surface presses with almost no force. But just a few meters down, the push becomes noticeable. At the very bottom of the reservoir, the water must support the weight of the entire column of water above it. This creates an intense outward pressure that is strongest at the deepest point.

A dam must be stable and resist toppling over from this powerful push. The massive, broad base serves two critical functions. First, the sheer volume of material provides the strength to withstand the immense pressure trying to rupture the wall at its lowest point. Second, the wide foundation anchors the entire structure, preventing the dam from being tipped forward by the water’s force. The shape is essentially a wedge, with the thick end facing the source of the pressure, ensuring it remains firmly planted.

In essence, the dam’s design mirrors the pressure profile of the water itself. It is a direct and logical response to a force that grows steadily stronger with depth, ensuring the structure remains immovable against the tremendous weight it contains.

Question  22. 

Why do sea divers need special protective suit?
Ans:

Sea divers wear protective suits not as a mere uniform, but as a mobile life-support system that recreates the essential conditions of the surface world. The deep ocean is a fundamentally hostile environment for humans, and the suit is our crucial barrier against its three primary assaults: cold, pressure, and physical danger.

The first and most immediate threat is cold. Water draws heat away from the body nearly 25 times faster than air. Even in tropical waters, the temperature a few meters below the surface can be shockingly low, quickly sapping a diver’s body heat and leading to dangerous hypothermia. The protective suit, especially a wetsuit, fights this by trapping a thin layer of water between the diver’s skin and the neoprene rubber. The diver’s body warms this trapped water, and the insulating material of the suit drastically slows down the process of heat loss, turning the water itself into a warm, stable barrier.

The second, more insidious threat is pressure. For every 10 meters a diver descends, the pressure increases by one atmosphere. This immense squeeze doesn’t just compress the air in their lungs; it compresses the entire body. Without a suit, this pressure would be directly transmitted to the diver’s skin and tissues. A well-fitted suit, particularly a rigid drysuit, creates a protective layer that helps the body resist and manage this crushing force, acting as a flexible exoskeleton against the weight of the ocean.

Finally, the suit provides essential physical protection. The underwater world is not a smooth, empty swimming pool. It is full of potential hazards—razor-sharp coral, jagged rocks, stinging jellyfish, or abrasive surfaces on shipwrecks. A simple scrape that would be minor on land can become a serious, infection-prone wound in the saltwater environment. The tough material of the dive suit acts as a robust shield, preventing cuts, scrapes, and stings that could otherwise cut a dive short or lead to a medical emergency.

In essence, the diver’s suit is a portable pocket of human habitability, allowing us to briefly visit a world we were not built to inhabit. It keeps us warm, helps our bodies cope with crushing pressure, and shields our fragile skin from a landscape of hidden dangers.

Question  23. 

State the laws of liquid pressure.

Ans:

The laws that govern how pressure behaves within a liquid are fundamental to understanding fluid mechanics. They can be summarized as follows:

1. The Law of Depth: Pressure within a liquid increases with depth. The deeper you go, the greater the weight of the liquid above you, resulting in higher pressure.
2. The Law of Equality at a Level: At any point within a body of liquid at rest, the pressure is the same in all directions. Furthermore, all points lying on the same horizontal level inside the liquid experience the same pressure.
3. The Law of Direction: The pressure exerted by a liquid is always perpendicular (at a right angle) to the surface of the object or container it is in contact with. It does not push sideways against the walls.
4. The Law of Container Shape: The pressure at a given depth depends only on the depth and the density of the liquid; it is completely independent of the shape, size, or volume of the container.
5. The Law of Transmitted Force (Pascal’s Law): When pressure is applied to a confined liquid at any point, it is transmitted equally and undiminished in all directions throughout the liquid. This principle is what allows hydraulic systems to multiply force.

Question  24. 

A tall vertical cylinder filled with water is kept on a horizontal table top. Two small holes A and B are made on the wall of the cylinder, A near the middle and B just Below the free surface of water. State and explain your observation.

Ans:

Observation: You would observe that the water jet streaming from hole B (just below the surface) is slow, weak, and travels only a short distance horizontally before curving down to the table. In contrast, the water jet from hole A (near the middle) is fast, forceful, and shoots out to a significantly longer horizontal distance.

Explanation:

The reason for this striking difference lies in how water pressure within the cylinder changes with depth.

Imagine the water in the cylinder as a column. The weight of all the water above a certain point pushes down on the water below it. This creates pressure.

• At hole B, very close to the surface, there is only a small amount of water above it pushing down. Therefore, the pressure at point B is low.
• At hole A, near the middle of the cylinder, a much taller column of water sits above it. The weight of this column creates a high pressure at point A.

When the holes are opened, this internal pressure is what propels the water outwards. The water is pushed out more forcefully from the high-pressure region than from the low-pressure one.

This difference in force translates directly to the speed of the exiting water. The high pressure at A forces the water out with a high initial speed, allowing it to travel a long, flat arc. The low pressure at B results in a slow, sluggish flow that cannot overcome the pull of gravity for long and falls almost straight down.

In essence, the water jet at the bottom “wins” the race in distance and force, not because of its position, but because it carries the energy of the greater weight of water pressing down from above.

Question  25. 

(a)How does the liquid pressure on a diver change if: the diver moves to the greater depth

(b) How does the liquid pressure on a diver change if : The diver moves horizontally?

Ans:

(a) When the diver moves to a greater depth:

The liquid pressure on the diver increases significantly.

This happens because a diver submerged in water is supporting the weight of all the water directly above them. Imagine the water as a tall, heavy column standing on the diver’s shoulders. As the diver swims deeper, the height of this water column increases, making it taller and heavier.

Since pressure is caused by the weight of the fluid, carrying this heavier “column” of water results in a greater force being exerted on every part of the diver’s body. The deeper the diver goes, the more water there is above them, and the more intensely the water presses in from all directions.

(b) When the diver moves horizontally:

The liquid pressure on the diver remains the same, provided they are moving at a constant depth.

This is because the pressure in a liquid at rest depends only on the depth below the surface and the density of the liquid, not on horizontal position. Whether the diver is one meter away from their starting point or ten meters away, if they are swimming along at the same depth, the height of the water column above them remains unchanged.

The water is pushing down on them with the same force regardless of their horizontal location. Therefore, the squeezing pressure they feel from the water does not change as they move sideways.

Question  26. 

State Pascal’s law of transmission of pressure.

Ans:

The Fundamental Rule of Contained Fluids

Imagine you have a fluid—a liquid or a gas—that is perfectly trapped inside a container without any air bubbles. This fluid isn’t just sitting there passively; it has a special rule governing how it handles any pressure you apply to it.

This rule states that when you apply a squeezing force (pressure) at any single point on a confined fluid that is not moving, this change in pressure is not absorbed in just that one spot. Instead, the fluid acts as a perfect messenger, transmitting that exact same pressure change to every other part of the container’s walls and to every single molecule within the fluid itself. The strength of this pressure is felt equally in all directions, throughout the entire system.

In its simplest terms: A push you give at one end is felt as an identical push everywhere else, instantly and without loss.

The Magic in Action: A Practical Example

The real power of this principle is how it allows us to multiply force. Think of a simple hydraulic car jack.

1. It consists of two cylinders connected by a pipe and filled with oil. One cylinder has a small piston (let’s say 1 square centimeter), and the other has a large piston (say 100 square centimeters).
2. When you push down on the small piston with a force equivalent to 1 kilogram, you are applying pressure to the oil.
3. According to the principle, this exact same pressure is transmitted undiminished to the large piston.
4. Here’s the transformation: The pressure (force per unit area) arriving at the large piston is the same, but because its area is 100 times larger, the total force it pushes upward with is 100 times greater.

So, your 1 kg of force on the small piston becomes 100 kg of lifting force on the large piston. You’ve traded a small movement over a long distance on your end for a massive force over a short distance on the other end. This is the secret behind hydraulic machinery like brakes, excavators, and presses, where a small input force is used to generate a tremendously powerful output.

Question  27. 

Name two applications of Pascal’s law.

Ans:

1. Industrial Hydraulic Press for Molding Plastics
A primary application is found in large-scale industrial presses used for molding thermoplastics and composite materials. The system uses a confined fluid and two pistons of vastly different sizes. A comparatively small force applied to the small piston generates immense pressure in the fluid. According to Pascal’s law, this pressure is transmitted undiminished to a much larger piston. The large piston then exerts a massive, uniform force, pressing the raw plastic granules inside a mold. This ensures the material is compressed evenly into every detail of the mold cavity, creating consistently dense and intricately shaped plastic components.

2. Hydraulically-Adjustable Hospital Beds
The principle is crucial in the operation of hydraulically adjustable hospital beds. These beds use a network of fluid-filled cylinders connected by narrow pipes. When a caregiver activates a pump or control valve, it applies pressure to the fluid at one end of the system. This pressure transmits instantly throughout the confined fluid, as per Pascal’s law, causing pistons within the cylinders to extend or retract. This action smoothly and quietly lifts, lowers, or articulates different sections of the bed mattress. This allows for precise patient positioning for medical procedures, comfort, or safe entry and exit, all powered by the efficient transmission of fluid pressure.

Question  28. 

Explain the principle of a hydraulic machine. Name two devices which work on this principle.

Ans:

The Core Principle: Power Through Liquid Push

At its heart, a hydraulic machine works by using a liquid’s unique property to transfer and multiply force. Unlike air, a liquid is very difficult to squeeze into a smaller space; it is essentially incompressible. When you push on a liquid in a closed container, it doesn’t absorb the energy by compressing. Instead, it transmits that push, or pressure, equally and instantly in all directions.

Think of it like a water-filled balloon. If you press on one spot, the bulge and the pressure immediately move to another part of the balloon.

This is the key: A force applied to one part of a confined liquid shows up as pressure everywhere, allowing you to redirect that force to another location.

The Force Multiplier Effect

This is where the real power comes in. Most hydraulic machines use two pistons of different sizes, housed in connected cylinders filled with fluid.

1. This creates pressure in the fluid.
2. Because the pressure is the same everywhere, that same pressure now acts on a much larger piston.
3. Since Force = Pressure x Area, the larger piston has a much larger area. With the same pressure, it generates a much larger output force.

It’s a trade-off: the larger piston will move a shorter distance than the smaller one, but it will do so with massively increased force. You are essentially trading “distance moved” for “power gained.”

Question  29. 

Name and state the principle on which a hydraulic press works. Write one use of hydraulic press.

Ans:

The core idea behind every hydraulic press is a fundamental rule of fluid behavior known as Pascal’s Principle.

This principle explains that a liquid trapped in a sealed space does not compress easily. When you push on it by applying pressure at one point, that push travels undiminished through every part of the liquid. The fluid acts as a perfect messenger for force.

A hydraulic press puts this idea into practice with a simple yet powerful design. It uses two cylinders—one significantly wider than the other—linked together and filled with a sturdy oil. If you exert a modest force on the smaller piston, it creates pressure within the oil. Because the liquid cannot be squeezed into a smaller space, this same pressure is delivered entirely to the face of the larger, second piston.

Here is where the magic of scale happens. Pressure is defined as force spread over an area. The larger piston presents a much greater surface area for the fluid to push against. Since it experiences the same pressure as the small piston, the total upward force it can produce is multiplied dramatically. This mechanical advantage allows a person to generate a crushing force capable of bending steel.

A common industrial application of this power is in vehicle recycling yards. Hydraulic presses are the muscle behind car crushers, which efficiently flatten end-of-life automobiles into dense, stackable bundles of scrap metal, making transportation and processing far more efficient.

Question  30. 

The diagram below in Fig. 4.12 shows a device which makes the use of the principle of transmission of pressure.

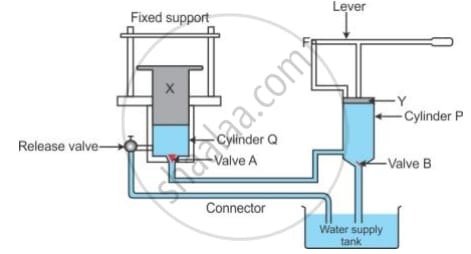
1. Name the parts labelled by the letters X and Y.

2. Describe what happens to valves A and B and to the quantity of water in the two cylinders when the lever arm is moved down.

3. Give reasons for what happens to valves A and B in part (ii).

4. What happens when the release valve is opened?

5. What happens to valve B in cylinder P when the lever arm is moved up?

6. Give a reason for your answer in part (v).

7. State one use of the above device.

Ans:

1. Name the parts labelled by the letters X and Y.

• X: Load Piston or Ram (the part that lifts the load in Cylinder Q).
• Y: Pump Piston (the part moved by the lever in Cylinder P).

2. Describe what happens to valves A and B and to the quantity of water in the two cylinders when the lever arm is moved down.

• Valve A: It opens.
• Valve B: It closes.
• Water in Cylinder P: Decreases, as it is forced out.
• Water in Cylinder Q: Increases, as water is forced into it from Cylinder P.

3. Give reasons for what happens to valves A and B in part (ii).

• The downward movement of the lever increases the pressure in Cylinder P.
• This high pressure forces Valve B to close (to prevent water from returning to the supply tank) and simultaneously forces Valve A to open, allowing the pressurized water to flow into Cylinder Q.

4. What happens when the release valve is opened?

• Opening the release valve provides a path for the pressurized water in Cylinder Q to escape back to the water supply tank.
• The pressure in Cylinder Q drops, and the weight of the load on the ram (X) pushes it down, forcing the water out and lowering the load.

5. What happens to valve B in cylinder P when the lever arm is moved up?

• Valve B opens.

6. Give a reason for your answer in part (v).

• Lifting the lever arm reduces the pressure in Cylinder P, creating a partial vacuum or low-pressure area.
• The higher pressure from the water supply tank pushes water up through the connector, forcing Valve B to open and fill Cylinder P with water. Valve A closes during this action to prevent water from flowing back from Cylinder Q.

7. State one use of the above device.

• The device is a hydraulic jack, used for lifting heavy objects, such as a car to change a tire.

Question  31. 

Draw a simple diagram of a hydraulic jack and explain its working.
Ans:

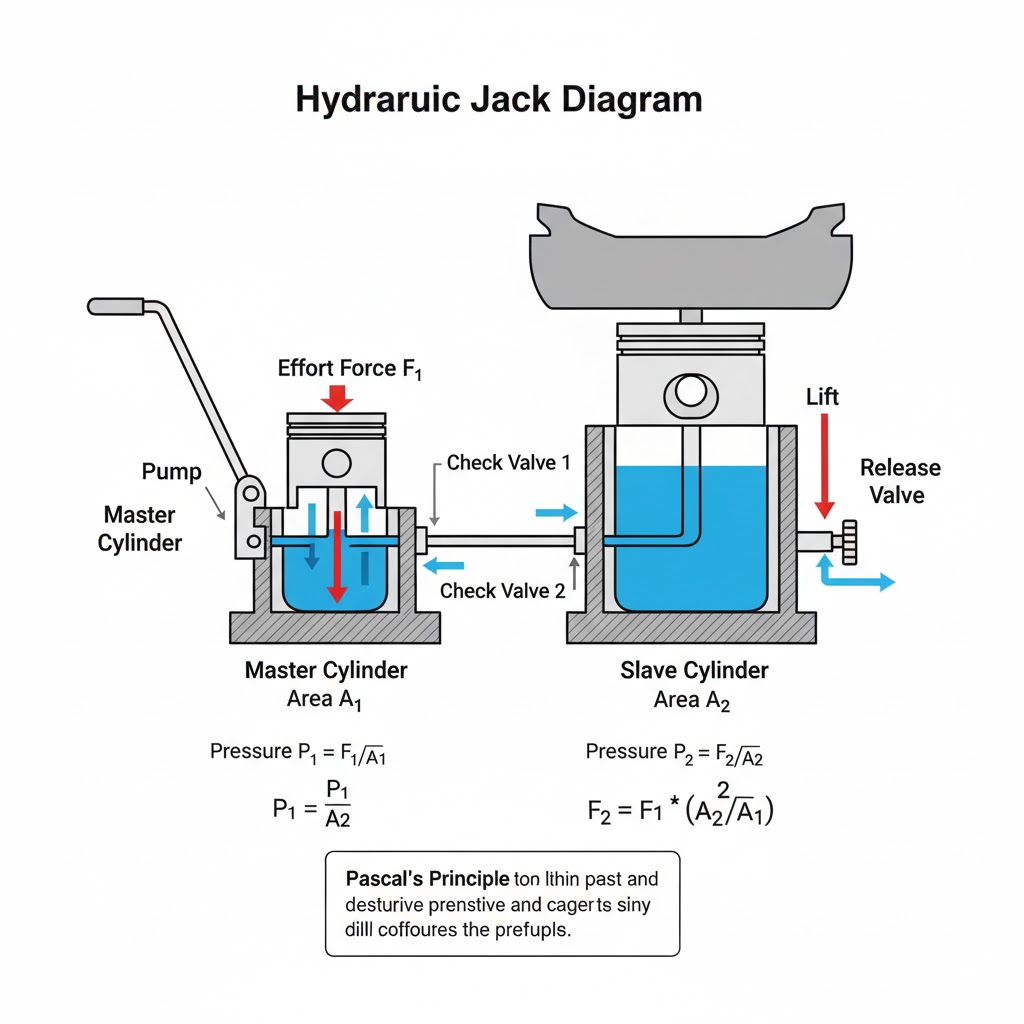
The Mechanics of a Hydraulic Jack

A hydraulic jack is a masterclass in practical physics, transforming modest human effort into enough power to lift a vehicle. Its core operation is a cycle of building, transferring, and releasing pressure, all governed by a fundamental law of fluids.

The Core Principle: Force Multiplication

At the heart of the system is Pascal’s Principle, which states that pressure applied to a confined fluid is transmitted undiminished in every direction. The jack cleverly leverages this by using two different-sized pistons. The real trick lies in the relationship between Pressure, Force, and Area (P = F/A). While the pressure remains the same throughout the fluid, the force is a product of that pressure multiplied by the area it acts upon (F = P x A). A large surface area translates to a much greater output force from the same input pressure.

Stage 1: The Lifting Stroke (Building Power)

• User Action: You press the handle downward.
• Creating Pressure: This action drives the small pump piston inward, compressing the hydraulic oil trapped in its chamber. With the release valve sealed shut, the fluid has no escape route, causing its pressure to spike dramatically.
• Transferring Force: This highly pressurized oil is now forced through a passage into the main cylinder, directly underneath the much larger load piston (or ram).
• The Force Multiplier in Action: The same pressure now pushes upward against the massive surface area of the load piston. Because its area is many times larger than that of the pump piston, the resulting upward force is multiplied by a corresponding factor. This immense force lifts the heavy load.
• A Simple Comparison: Think of it as the reverse of a sharp needle. A needle concentrates a small force onto a tiny point to create extreme pressure for piercing. The hydraulic jack does the opposite: it takes a small force, uses it to create high pressure in a fluid, and then spreads that pressure over a large surface to generate a massive, lifting force.

Stage 2: The Reset Stroke (Preparing for the Next Lift)

• User Action: You pull the handle back up.
• Refilling the Pump: This retraction of the small pump piston creates a partial vacuum in the pump chamber. This drop in pressure causes a small inlet valve (a one-way gate) to open, drawing a fresh charge of oil from the reservoir into the chamber.
• Holding the Gain: Crucially, the main valve under the load piston stays shut during this process, locking the oil in the main cylinder and preventing the load from sinking. Each complete cycle of Stage 1 and 2 pushes a little more oil under the ram, raising the load incrementally with every pump.

Stage 3: The Controlled Descent (Lowering the Load)

• User Action: You gradually unscrew or open the release valve.
• Releasing the Pressure: This action creates an escape route for the trapped, high-pressure oil beneath the load piston, allowing it to flow back into the main fluid reservoir.
• Managing the Descent: As the oil evacuates, the pressure in the main cylinder drops. The weight of the load itself then pushes the ram downward, expelling the fluid. By carefully adjusting how much the release valve is open, you precisely control the flow of oil and, consequently, the speed at which the load is lowered, ensuring a smooth and safe descent.

In Essence

Fundamentally, a hydraulic jack is a trade-off. It exchanges a large, repeated movement of the small pump piston for a smaller, but immensely powerful, movement of the large load piston. Your repetitive effort is converted into fluid pressure, which the machine then translates back into a colossal mechanical force, making the impossible task of lifting a car as simple as pumping a handle.

Question  32. 

Explain the working of a hydraulic brake with a simple labelled diagram.

Ans:

Here’s a simple labelled diagram of a hydraulic brake system:

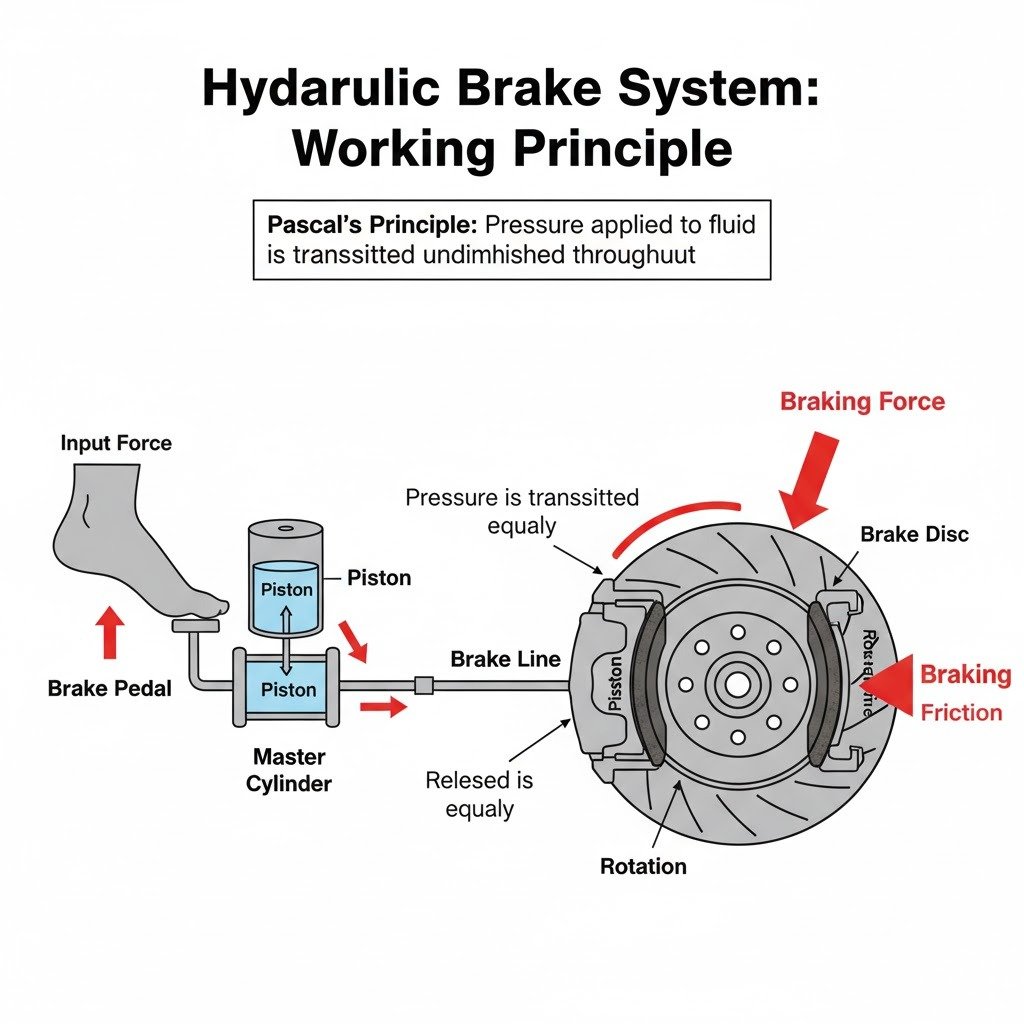
Working of a Hydraulic Brake System:

Hydraulic brakes also operate on Pascal’s Principle, allowing a small force applied by the driver to translate into a large braking force at the wheels.

1. Brake Pedal and Master Cylinder: When the driver presses the brake pedal, this action pushes a piston within the master cylinder.
2. Pressure Generation: This movement of the piston creates pressure in the brake fluid (an incompressible hydraulic fluid) contained within the master cylinder.
3. Pressure Transmission: According to Pascal’s Principle, this pressure is transmitted equally and undiminished through the brake lines (tubes) to the individual slave cylinders located at each wheel.
4. Braking at the Wheels:
   • In a disc brake system (as shown in the diagram), the pressure from the fluid pushes pistons within the caliper.
   • These caliper pistons then force the brake pads to clamp onto the rotating brake disc (rotor) attached to the wheel.
   • The resulting friction between the pads and the disc generates a braking force that slows down and eventually stops the wheel.
   • In drum brake systems, the pressure pushes brake shoes against the inside of a rotating drum.
5. Releasing the Brakes: When the driver releases the brake pedal, the pressure in the system drops. Springs in the master cylinder and at the wheels pull the pistons and brake pads/shoes back to their original positions, disengaging the braking force.

This system ensures that even a moderate force on the brake pedal can effectively stop a heavy vehicle, as the pressure is multiplied by the larger surface area of the pistons in the slave cylinders compared to the master cylinder.

Question 33. 

(a) Complete the following sentence : Pressure at a depth h in a liquid of density p is ………………….

(b) Complete the following sentence : Pressure is ……………….. in all directions about a point in a liquid.

(c)Complete the following sentence : Pressure at all points at the same depth is ………………..

(d) Complete the following sentence : Pressure at a point inside the liquid is …………………. To its depth.

(e)Complete the following sentence : Pressure of a liquid at a given depth is ……………… To the density of the liquid.

Ans:

(a) Complete the following sentence : Pressure at a depth h in a liquid of density p is h pg(where g is the acceleration due to gravity).

(b) Complete the following sentence : Pressure is equal in all directions about a point in a liquid.

(c) Complete the following sentence : Pressure at all points at the same depth is the same (or equal).

(d) Complete the following sentence : Pressure at a point inside the liquid is directly proportional to its depth.

(e) Complete the following sentence : Pressure of a liquid at a given depth is directly proportional to the density of the liquid.

Exercise 4 (A)

Question 1. 

The S.I. unit of pressure is : 

1. N cm-2
2. Pa
3. N
4. N m2

Question 2. 

The pressure inside a liquid of density p at a depth h is : 

1. h ρ g
2. ℎ /ρ⁢𝑔
3. ℎ⁡ρ /𝑔
4. ℎ⁡ρ

Question 3. 

The pressure P1 at a certain depth in river water and P2 at the same depth in sea water are related as :

1. P1 > P2
2. P1= P2
3. P1 < P2
4. P1 –  P2 = atmospheric pressure

Question 4. 

The pressure P1 at the top of a dam and P2 at a depth h form the top inside water (density p) are related as : 

1. P1 > P2
2. P1 = P2
3. P1 –  P2 = h ρ g
4. P2 –  P1 = h ρ g

Exercise 4 (A)

Question 1. 

A hammer exerts a force of 1.5 N on each of the two nails A and B. The area of the cross section of tip of nail A is 2 mm2 while that of nail B is 6 mm2. Calculate pressure on each nail in pascal.

Ans:

When a hammer drives a nail, the force it applies is only part of the story. The real difference comes from the nail’s tip. A smaller contact area results in a much more concentrated pressure, which is why sharp nails pierce wood so easily.

Let’s break down the problem. We know:

• Force on each nail, F = 1.5 N
• Cross-sectional area of nail A’s tip, A_A = 2 mm²
• Cross-sectional area of nail B’s tip, A_B = 6 mm²

Pressure (P) is calculated using the formula:
P = F / A

Since the pressure needs to be in pascals (Pa), and 1 pascal = 1 newton per square meter (N/m²), our first job is to convert the areas from mm² to m².

• 1 mm² = 1 × 10⁻⁶ m² (because 1 m = 1000 mm, so 1 m² = 1,000,000 mm²)

For Nail A:

• Area in m², A_A = 2 mm² = 2 × 10⁻⁶ m²
• Pressure, P_A = F / A_A = 1.5 N / (2 × 10⁻⁶ m²)
• P_A = 750,000 Pa or 7.5 × 10⁵ Pa

For Nail B:

• Area in m², A_B = 6 mm² = 6 × 10⁻⁶ m²
• Pressure, P_B = F / A_A = 1.5 N / (6 × 10⁻⁶ m²)
• P_B = 250,000 Pa or 2.5 × 10⁵ Pa

In Summary:

Even though the same force is applied to both nails, the pressure exerted on the wood is vastly different.

• The pressure under Nail A is 750,000 Pascals.
• The pressure under Nail B is 250,000 Pascals.

This demonstrates a key principle: for an equal force, pressure increases as surface area decreases. Nail A, with its finer point, experiences three times the pressure of Nail B, allowing it to penetrate materials with greater ease.

Question 2. 

A block of iron of mass 7.5 kg and of dimensions 12 cm × 8 cm × 10 cm is kept on a table top on its base of side 12 cm × 8 cm.

Calculate: Thrust and Pressure exerted on the table top Take 1 kgf = 10 N.

Ans:

The thrust exerted by the iron block on the table top is equal to its weight. The mass of the block is 7.5 kg, and using the conversion 1 kgf = 10 N, the weight is calculated as follows:
Weight = mass × g = 7.5 kg × 10 N/kg = 75 N.
Thus, the thrust is 75 N.

The pressure exerted is the thrust per unit area. The base in contact with the table has dimensions 12 cm × 8 cm. Converting to meters: 12 cm = 0.12 m, 8 cm = 0.08 m. The area is:
Area = 0.12 m × 0.08 m = 0.0096 m².
Pressure = thrust / area = 75 N / 0.0096 m² = 7812.5 N/m² (or Pascals).

Therefore, the thrust is 75 N and the pressure is 7812.5 N/m².

Question 3.

A vessel contains water up to a height of 1.5 m. Taking the density of water 103 kg m-3, acceleration due to gravity 9.8 m s-2 and area of base of the vessel 100 cm2, calculate: (a) the pressure and (b) the thrust at the base of the vessel.

Ans:

Question 4. 

The area of base of a cylindrical vessel is 300 cm2. Water (density= 1000 kg m-3) is poured into it up to a depth of 6 cm. Calculate : (a) the pressure and (b) the thrust of water on the base. (g = 10m s-2.

Ans:

Question 5. 

Calculate the height of a water column which will exert on its base the same pressure as the 70 cm column of mercury. The density of mercury is 13.6 g cm-3.

Will the height of the water column in part (a) change if the cross-section of the water column is made wider?

Ans:

(a) Calculating the Height of the Water Column

The pressure exerted by a liquid column depends on its height, density, and gravity, and is given by the formula:

Pressure, P = h ρ g

Where:

• h is the height of the liquid column.
• ρ (rho) is the density of the liquid.
• g is the acceleration due to gravity.

We are told that the pressure from the water column must equal the pressure from the mercury column. So, we can set their pressure equations equal to each other.

Pressure from Mercury = Pressure from Water
(h ρ g)_mercury = (h ρ g)_water

Since the acceleration due to gravity ‘g’ is the same for both, it cancels out from both sides of the equation.

(h_mercury × ρ_mercury) = (h_water × ρ_water)

Now we can plug in the values we know:

• h_mercury = 70 cm
• ρ_mercury = 13.6 g/cm³
• ρ_water = 1.0 g/cm³ (This is the standard density of water)

Calculation:
h_water = (h_mercury × ρ_mercury) / ρ_water
h_water = (70 cm × 13.6 g/cm³) / 1.0 g/cm³
h_water = 952 cm

Therefore, a water column of 952 cm will exert the same pressure on its base as a 70 cm column of mercury.

(b) Will the height change if the water column is made wider?

No, the height of the water column will not change if its cross-section is made wider.

Reasoning:

The pressure at the base of a liquid column is determined by the weight of the liquid directly above it per unit area. Making the column wider increases the total volume and total weight of the water.

However, it also increases the area of the base over which this total weight is distributed. These two effects—increased force and increased area—cancel each other out perfectly.

The formula P = h ρ g shows that pressure depends only on the height (‘h’) and the density (‘ρ’) of the liquid (and ‘g’, which is constant). It is completely independent of the shape or the cross-sectional area of the container. A wide column and a narrow column of the same liquid and the same height will always exert the same pressure at their base.

Question 6. 

The pressure of water on the ground floor is 40,000 Pa and on the first floor is 10,000 Pa. Find the height of the first floor. (Take : density of water = 1000 kg m-3, g = 10 m s-2)

Ans:

Calculating Floor Height Using Water Pressure

The difference in water pressure measured on two floors of a building acts like a natural gauge for the vertical distance between them. In this scenario, the pressure drops from 40,000 Pascals on the ground floor to 10,000 Pascals on the first floor.

This means the weight of the water in the pipes between the two floors creates a pressure difference of:

30,000 Pascals

This number isn’t arbitrary; it is the direct result of the height of the water column. To find the height, we use the principle that the pressure from a fluid column is given by the product of its density, the force of gravity, and its height.

Setting up the relationship gives us:

Pressure Difference = (Density of Water) x (Gravity) x (Height Difference)

Plugging our known values into this equation looks like this:

30,000 = 1000 x 10 x Height Difference

Simplifying the multiplication on the right side gives us:

30,000 = 10,000 x Height Difference

To solve for the height, we simply rearrange the equation:

Height Difference = 30,000 / 10,000

This calculation provides a clear result:

Height Difference = 3 meters

In summary: The 30,000 Pascal pressure loss corresponds precisely to a 3-meter vertical climb of the water pipes from the ground floor to the first floor. This measurement reveals the functional height of the water column within the building’s structure, not necessarily the ceiling height.

Question 7. 

A simple U tube contains mercury to the same level in both of its arms. If water is poured to a height of 13.6 cm in one arm, how much will be the rise in mercury level in the other arm?

Given : density of mercury = 13.6 x 103 kg m-3 and density of water = 103 kg m-3.

Ans:

When water is added to one arm of the U-tube, it disrupts the equilibrium because water is less dense than mercury. The system compensates for this by shifting the mercury levels. A key point to remember is that mercury is incompressible; the volume that drops in one arm must equal the volume that rises in the other. This means if the mercury level in the arm with water falls by a certain distance, the level in the clean arm will rise by that same distance. The total difference in height between the two mercury surfaces will therefore be twice that distance.

We can find this distance by comparing the pressures at the same horizontal level within the mercury, right at the interface where the two liquids meet. At this level in the arm containing water, the pressure is due to the weight of the 13.6 cm water column pushing down. In the other arm, the pressure at the same level is determined solely by the excess column of mercury.

For the system to be balanced, these two pressures must be equal. This gives us the relationship:

(Density of Water) × (Height of Water Column) = (Density of Mercury) × (Height Difference of Mercury)

We know the density of mercury is 13.6 times greater than that of water. Plugging this in:

(1) × (13.6 cm) = (13.6) × (Height Difference)

From this, we can see directly that the Height Difference of the mercury levels is 1.0 cm.

Since this total height difference of 1.0 cm is created by the mercury level dropping in one arm and rising in the other by equal amounts, we know that each change is half of this total. Therefore, the mercury level in the arm without water rises by 0.5 cm.

Question 8. 

In a hydraulic machine, a force of 2 N is applied on the piston of area of cross section 10 cm2. What force is obtained on its piston of area of cross section 100 cm2 ?

Ans:

Question 9. 

What should be the ratio of area of cross section of the master cylinder and wheel cylinder of a hydraulic brake so that a force of 15 N can be obtained at each of its brake shoes by exerting a force of 0.5 N on the pedal ?

Ans:

The operational principle of a hydraulic brake is a direct application of Pascal’s law, where a pressure change in an enclosed fluid is conveyed without reduction to every part of the fluid and the container walls. This ensures the pressure within the master cylinder (P_m) is identical to the pressure within the wheel cylinder (P_w), establishing the foundational equality P_m = P_w.

Since pressure is defined as force exerted per unit area (P = F/A), this equality can be expressed in terms of the forces and areas involved:

F_m / A_m = F_w / A_w

In this scenario, a modest input force (F_m) of 0.5 Newtons is applied to the master cylinder. This force is responsible for creating the initial pressure in the system. The task is to determine the output force (F_w) of 15 Newtons at the wheel cylinder, which acts directly on the brake shoe.

To find the necessary relationship between the cylinders’ cross-sectional areas, we rearrange the equation:

A_m / A_w = F_m / F_w

Substituting the given values:

A_m / A_w = 0.5 N / 15 N = 1/30

This calculation reveals that the cross-sectional area of the master cylinder is only one-thirtieth the size of the wheel cylinder’s area. This deliberate disproportion in area is the key to force multiplication, enabling a small input force at the brake pedal to generate a significantly larger output force at the brakes, effectively stopping the vehicle.

Question 10. 

The areas of pistons in a hydraulic machine are 5 cm2 and 625 cm2. What force on the smaller piston will support a load of 1250 N on the larger piston? State any assumption which you make in your calculation.

Ans:

Analysis of the Hydraulic Force Multiplier

This hydraulic device operates on a straightforward yet powerful physical concept: a small force can balance a much larger one through the strategic use of pressure. The underlying rule is that within a confined liquid, pressure applied at one point is felt equally throughout the entire fluid.

The Governing Principle

The core idea can be summarized as follows: The pressure generated on the small piston must be equal to the pressure experienced by the large piston. Pressure is the amount of force spread over a given area.

This gives us the relationship:

Force on Small Piston / Area of Small Piston = Force on Large Piston / Area of Large Piston

Applying the Numbers

We are given:

• Target Load (F₂): 1250 N (the weight to be supported)
• Area of Large Piston (A₂): 625 cm²
• Area of Small Piston (A₁): 5 cm²
• Required Input Force (F₁): Unknown

To find the needed input force, we rearrange the principle:

F₁ = (F₂ × A₁) / A₂

Plugging in the values:

F₁ = (1250 N × 5 cm²) / 625 cm²

First, we multiply the top line: 1250 × 5 = 6250

Then, we divide by the area of the large piston: 6250 / 625 = 10

The Result

F₁ = 10 N

Interpreting the Outcome

This calculation reveals the machine’s remarkable efficiency. An input force of just 10 Newtons—which is about the force needed to lift a one-kilogram bag of sugar—is capable of supporting a massive 1250 Newton load, equivalent to about 125 kilograms.

This force multiplication comes with a trade-off. To displace a small amount of fluid in the large cylinder and lift the heavy load by a little, the small piston must be pushed down a much greater distance. The device essentially trades a large movement with a small force for a small movement with a large force.

A Practical Consideration

For this calculation to hold true in a real-world scenario, we must assume an ideal system. This means we ignore energy losses from friction between the moving parts and assume the hydraulic fluid does not compress at all. In practice, a slightly higher force might be needed to initiate movement and overcome these real-world inefficiencies.

This principle is the foundation for countless applications, most commonly the hydraulic jack used for lifting vehicles.

Question 11.

(i) The diameter of neck and bottom of a bottle are 2 cm and 10 cm, respectively. The bottle is completely filled with oil. If the cork in the neck is pressed in with a force of 1.2 kgf, what force is exerted on the bottom of the bottle?

(ii) Name the law/principle you have used to find the force in part (a).

Ans:

Analysis of Force in a Hydraulic System

(i) Determining the Force on the Bottom

The scenario describes a closed hydraulic system where a force applied to a small area creates a pressure that is harnessed to produce a larger force on a larger area.

Step 1: Establishing the System’s Pressure
A force of 1.2 kgf is applied to a cork fitted in the neck of the bottle. The neck has a diameter of 2 cm, meaning its radius is 1 cm. The area of the cork that transmits this force into the oil is calculated as:

*Area_cork = π × (radius)² = π × (1 cm)² = π cm²*

The pressure generated on the oil by this action is the force divided by this area:

*Pressure = Force_cork / Area_cork = 1.2 kgf / π cm²*

This pressure value, once created, propagates uniformly throughout the entire body of the confined oil.

Step 2: Calculating the Resulting Force at the Bottom
The bottom of the bottle has a much larger diameter of 10 cm, giving it a radius of 5 cm. Its surface area is therefore:

*Area_bottom = π × (radius)² = π × (5 cm)² = 25π cm²*

The force pushing upward on the bottom is the direct product of the transmitted pressure and this large area:

Force_bottom = Pressure × Area_bottom

Substituting the values we have:

*Force_bottom = (1.2 kgf / π cm²) × (25π cm²)*

The π terms cancel out, simplifying the calculation to:

*Force_bottom = 1.2 kgf × 25 = 30 kgf*

Conclusion: The force exerted on the bottom of the bottle is 30 kgf.

(ii) The Underlying Scientific Principle

This force multiplication is a direct application of Pascal’s Principle.

Pascal’s Principle states that a change in pressure applied to an enclosed, incompressible fluid is transmitted undiminished to every portion of the fluid and to the walls of its container.

In this case, the pressure created at the neck by the cork is identically transmitted to the bottom surface. Because the bottom has 25 times the area of the neck, the fluid pressure exerts a force that is 25 times greater at that point. The system essentially converts a modest input force into a powerful output force, demonstrating the core concept of a hydraulic multiplier. The constancy of pressure across different areas is the key to this phenomenon.

Question 12. 

A force of 50 kgf is applied to the smaller piston of a hydraulic machine. Neglecting friction, find the force exerted on the large piston, if the diameters of the pistons are 5 cm and 25 cm respectively.

Ans:

The operating principle behind this hydraulic system is Pascal’s law, a fundamental concept in fluid mechanics. This law states that when pressure is applied to a fluid confined in an incompressible system, that pressure is transmitted with equal intensity in all directions. This means the pressure generated at one point will appear undiminished at every other point within the enclosed fluid.

In practical terms, pressure (P) is calculated as the amount of force (F) acting upon a given unit of area (A), expressed as P = F/A.

This relationship allows us to set up a powerful equivalence for a hydraulic system with two pistons:

The pressure created by the input force on the small piston equals the pressure experienced by the large piston.

This gives us the equation:
F₁ / A₁ = F₂ / A₂

Where:

• F₁ is the 50 kgf input force applied to the smaller piston.
• A₁ is the surface area of the smaller piston.
• F₂ is the unknown output force on the larger piston (what we are solving for).
• A₂ is the surface area of the larger piston.

Since the pistons are circular, their effective areas are calculated using the formula for the area of a circle, A = πr². However, since we are given diameters, it is more direct to use A = πd²/4.

Step 1: Calculate the Piston Areas

• For the small piston (diameter = 5 cm):
  A₁ = π × (5 cm)² / 4 = (25π)/4 cm²
• For the large piston (diameter = 25 cm):
  A₂ = π × (25 cm)² / 4 = (625π)/4 cm²

Step 2: Determine the Mechanical Advantage (Area Ratio)
The true force-multiplying capability of the system lies in the ratio of the two piston areas. The force is multiplied by this factor.

Area Ratio = A₂ / A₁ = (625π / 4) / (25π / 4)

Notice that the π and the 4 cancel out, simplifying beautifully to:
Area Ratio = 625 / 25 = 25

This result shows that the large piston has twenty-five times the surface area of the small piston.

Step 3: Calculate the Output Force
Because the pressure is equal throughout the fluid, the larger area results in a proportionally larger force. We can rearrange the original equation to solve for the output force:

F₂ = F₁ × (A₂ / A₁)

Substituting the known values:
F₂ = 50 kgf × 25
F₂ = 1250 kgf

Conclusion
Therefore, by applying a modest force of 50 kgf to the small piston, the system generates a significant force of 1250 kgf at the large piston. This demonstrates a mechanical advantage of 25, meaning the output force is twenty-five times greater than the input force. This core principle is what enables hydraulic jacks to lift vehicles and other massive objects with relative ease.

Question 13. 

Two cylindrical vessels fitted with pistons A and B of area of cross-section 8 cm2 and 320 cm2 respectively are joined at their bottom by a tube and they are completely filled with water. When a mass of 4 kg is placed on piston A, Find: the pressure on piston A, the pressure on piston B, and the thrust on piston B.

Ans:

Understanding Force Multiplication in a Hydraulic System

This scenario is a classic demonstration of how a hydraulic system acts as a force multiplier, using a confined liquid to amplify an input force. The principle at work is that a liquid is largely incompressible, meaning pressure applied to it in one location must be transmitted equally to all other parts of the confined system.

From a Small Force to a System-Wide Pressure

The process begins with the 4 kg mass placed on the smaller piston (Piston A). The first step is to determine the force this mass exerts.

• The force (F_A) is the product of mass and gravitational acceleration: 4 kg multiplied by 9.8 m/s², which equals 39.2 Newtons (N).

This force is not acting in isolation; it is distributed over the surface area of Piston A.

• The area of Piston A is 8 cm², which is equivalent to 0.0008 m².
• Pressure is defined as force per unit area. Therefore, the pressure generated on the liquid by Piston A is calculated as 39.2 N divided by 0.0008 m², resulting in 49,000 Pascals (Pa).

This newly generated pressure of 49,000 Pa now fills the entire hydraulic system. Because the liquid cannot be compressed, this same pressure value acts uniformly on every surface in contact with the liquid, including the much larger Piston B.

Converting Pressure Back into an Amplified Force

While the pressure is identical throughout the system, the effect on Piston B is dramatically different due to its size. We now calculate the resulting thrust, or force, on Piston B.

• The area of Piston B is 320 cm², which is 0.032 m².
• Force is calculated by multiplying pressure by the area over which it acts.
• Therefore, the thrust on Piston B (F_B) is 49,000 Pa multiplied by 0.032 m².

This calculation gives a force of 1,568 N.

The Final Result in Perspective

To summarize:

• Pressure at Piston A: 49,000 Pa
• Pressure at Piston B: 49,000 Pa
• Thrust on Piston B: 1,568 N

The system demonstrates a key trade-off: the smaller piston moves a greater distance to displace enough fluid to make the larger piston move a smaller distance. However, in exchange for this reduced movement, the force is significantly multiplied. A modest 39.2 N input force is transformed into a powerful 1,568 N output thrust—enough to lift a heavy object. This is the fundamental mechanism behind equipment like hydraulic car jacks and industrial presses.

Question 14.

What force is applied on a piston of area of cross section 2 cm2 to obtain a force 150 N on the piston of area of cross section 12 cm2 in a hydraulic machine?

Ans:

Exercise 4 (B)

 Question 1. 

What do you understand about atmospheric pressure?

Ans:

Our Invisible Ocean: Understanding Atmospheric Pressure

We often think of space as a vacuum, but we live our entire lives at the bottom of a deep, invisible ocean. This ocean isn’t made of water, but of air—a vast, dynamic mixture of gases we call the atmosphere. Atmospheric pressure is simply the weight of this colossal column of air pressing down on everything on the Earth’s surface.

Imagine stacking over 100 kilometers of air directly above your head. That immense stack has a real, measurable weight. At sea level, this force is so substantial that it exerts nearly 15 pounds of pressure on every single square inch of your body. That means the total air pressure on an average person is equivalent to the weight of a small car! We don’t collapse under this force because the fluids and gases inside our bodies push outward with an equal and opposite pressure.

We can’t feel this constant push, but we can easily observe its effects.

• The Drinking Straw: When you suck on a straw, you aren’t “pulling” the liquid up. You are actually removing some of the air from inside the straw, which lowers the air pressure there. The higher pressure of the atmosphere pushing down on the surface of the drink in your glass then forces the liquid up the straw and into your mouth.
• Your Ears “Pop”: When you drive up a mountain or take off in an airplane, you are moving up through layers of our “air ocean.” The column of air above you gets shorter, so it weighs less and the pressure decreases. The higher-pressure air trapped inside your inner ear pushes the eardrum outward, causing that familiar “pop” until the pressures equalize.
• Weather Patterns: Atmospheric pressure is the engine of weather. High-pressure systems, which are like heavy, dense domes of air, typically bring clear, calm skies. Low-pressure systems, which are lighter and less dense, allow air to rise, cool, and form clouds and storms. A barometer is essentially a weather “scale” that measures this weight.

Question 2. 

Write the numerical value of the atmospheric pressure on the surface of earth in pascal.

Ans:

The atmospheric pressure at the surface of the Earth, a measure known as one “standard atmosphere” (atm), is defined as precisely 101,325 pascals (Pa).

This value represents the average weight of the air column exerting force on a given area at sea level. For simpler calculations, this is often rounded to approximately 100,000 pascals or 10^5 Pa.

To put it in perspective, this means that every square meter of the Earth’s surface is under a force of about 100,000 newtons from the weight of the air above it.

Question 3. 

What physical quantity is measured in torr? How is it related to the S.I. unit of the quantity?

Ans:

Understanding the Torr as a Unit of Pressure

While the pascal is the official SI unit for pressure, a much older unit, the torr, remains deeply embedded in scientific practice, particularly in chemistry and medicine. Its existence is a direct legacy of a groundbreaking 17th-century experiment.

The unit is named for Evangelista Torricelli, who, in 1643, performed a simple yet revolutionary act. He filled a long glass tube with mercury and inverted it into a dish, also containing mercury. Instead of the tube emptying completely, a column of mercury remained suspended, with an empty space—a vacuum—left at the sealed top. Torricelli correctly deduced that it was the weight of the atmosphere pressing down on the dish’s surface that was propping up the mercury column inside the tube. The height of that column became the first true tool for measuring atmospheric pressure.

This is the origin of the torr. Essentially, one torr was conceived as the pressure exerted by a one-millimeter column of mercury (mmHg) under standard conditions. It provided an incredibly intuitive way to quantify pressure, as it could be read directly from a scale on a barometer or manometer.

The modern definition has been refined for precision but stays true to this concept. It is now formally defined as exactly 1/760th of one standard atmosphere. Since one standard atmosphere is scientifically defined as 101,325 pascals, the conversion is fixed:

1 torr = 101,325 / 760 Pascals ≈ 133.322 Pascals

In practical terms, this means a pressure reading in torr will always be a much more manageable number than its direct pascal equivalent, especially for pressures around our everyday atmospheric pressure. For instance, standard atmospheric pressure is a cumbersome 101,325 Pa, but a concise 760 torr. This convenience is why it has persisted for so long, turning a classic experiment into a lasting unit of measurement. You could think of it as a ruler, originally etched in mercury, that we still use to gauge the push of the air around us and the pressures in contained systems.

Question 4. 

Name the physical quantity which is expressed in the unit ‘atm’. State its value in pascal.

Ans:

The physical quantity expressed in the unit ‘atm’ is pressure.

Its value is defined as 101,325 pascals.

Question 5. 

We do not feel uneasy even under enormous pressure of the atmosphere above as well as around us. Give a reason.

Ans:

We do not feel the immense atmospheric pressure because the pressure inside our bodies—from our blood, fluids, and tissues—is perfectly balanced to push outward with an equal force. This internal pressure matches the external air pressure pressing in on us, creating a state of equilibrium where no net force crushes us. Essentially, we are built from the inside to naturally counterbalance the weight of the atmosphere.

Question 6. 

Describe an experiment to demonstrate that air exerts pressure.

Ans:

Defying Gravity: The Sealed Cup Mystery

This simple yet startling experiment challenges our everyday experience with gravity, revealing the constant, unseen force that surrounds us.

Setting Up the Challenge

Gather a stiff plastic cup and fill it completely with water, right to the very edge. The goal is to have a smooth, bulging meniscus of water with no air pocket left inside. Next, take a smooth, rigid plastic sheet or a heavyweight index card and carefully slide it over the entire rim. The key is to ensure the entire edge of the cup makes contact, creating a temporary seal. With one hand securing the sheet firmly against the cup, swiftly flip the entire assembly upside-down over a sink. Once inverted, you can cautiously release your grip.

The Astonishing Result

Contrary to all expectation, the water remains trapped inside the upturned cup. The plastic sheet clings to the rim as if glued, defying the downward pull of gravity on the water. It appears that an invisible barrier is holding everything in place.

Unmasking the Invisible Force

The secret lies not in the cup or the sheet, but in the ocean of air we live in. Our atmosphere, a thick layer of gases, has weight and exerts pressure on every surface it touches. This atmospheric pressure is substantial, but we don’t usually notice it because it pushes equally in all directions.

When you invert the cup, two main forces compete:

1. The Downward Pull: This is the combined weight of the water in the cup, plus the very slight pressure from the tiny amount of air trapped inside (if any).
2. The Upward Push: This is the tremendous force of atmospheric pressure pressing upwards against the underside of the plastic sheet.

The outcome of this quiet battle is almost always a victory for the air. The upward push from the outside air pressure is significantly greater than the combined downward forces of the water’s weight and the minimal internal air pressure. The atmosphere effectively pins the sheet to the cup’s rim, creating a seal strong enough to hold the water at bay. This dramatic demonstration makes the intangible concept of air pressure suddenly visible and undeniable, proving that what seems like empty space is actually a powerful physical presence.

Question 7. 

(a) Explain the following : A balloon collapses when air is removed from it.

(b) Explain the following : Water does not run out of a dropper unless its rubber bulb is pressed .

(c) Explain the following : Two holes are made in a completely filled sealed tin can to take out oil from it .

Ans:

(a) Why does a balloon collapse when air is removed from it?

Think of the air inside a blown-up balloon as an invisible scaffold pushing outwards against the balloon’s rubber. The air molecules are constantly moving and colliding with the inner walls, creating internal pressure that stretches the rubber taut.

When you remove this air, you are dismantling that internal scaffold. The number of air molecules inside decreases dramatically, which means there are far fewer collisions happening against the inner surface. This causes the internal pressure to drop significantly.

Now, the ever-present air from the outside, which is at a much higher pressure, is no longer being balanced by the push from the inside. This unbalanced external atmospheric pressure presses uniformly from all sides, forcefully squeezing the flexible rubber inwards until it crumples and collapses completely. Essentially, the outside air crushes the balloon the moment its internal support system is taken away.

(b) Why does water not run out of a dropper unless its rubber bulb is pressed.

This is a clever demonstration of how air pressure can act as a gatekeeper. When you fill a dropper and hold it vertically, you might expect gravity to pull the water down. However, two forces are at play.

The water inside the dropper does indeed push down, but it also creates a small, empty space (a vacuum) at the top of the tube, right beneath the bulb. The outside air, at atmospheric pressure, pushes upwards against the tiny opening at the bottom of the dropper. This upward push from the outside air is stronger than the combined weight of the water and the slight pull of the vacuum above it. The result is a perfect balance of forces, and the water is held securely inside, trapped by the invisible seal of atmospheric pressure.

Pressing the rubber bulb changes everything. You are now compressing the air inside the dropper, increasing its pressure. This man-made pressure becomes greater than the outside air pressure pushing up from the bottom. This imbalance forces the water out of the dropper, breaking the seal. It’s like you are actively overpowering the atmospheric gatekeeper to let the water through.

(c) Why two holes are made in a completely filled sealed tin can to take out oil from it.

Imagine a sealed can full of oil. It’s a solid, continuous block of liquid with no air inside. If you make only one hole and try to pour, the oil might glug out slowly or not at all. This is because as the oil flows out, it leaves an empty space behind. Nature abhors a vacuum, and with no air to fill this space, a low-pressure area forms inside the can.

The outside air, which is at a higher pressure, pushes against the stream of oil trying to exit, effectively blocking it. The oil needs the outside air to come in and take its place to flow smoothly.

This is where the second hole comes in. It acts as an air vent. As oil pours out from the first hole, air can freely enter through the second hole. This incoming air fills the space left by the departing oil, equalizing the pressure inside the can with the atmospheric pressure outside. With the pressure balanced, gravity can pull the oil out smoothly and continuously without any resistance from the air, allowing for a steady, uninterrupted stream. One hole is for the liquid to get out; the other is for the air to get in, making the flow possible.

Question 8. 

Why does the liquid rise in a syringe when its piston is pulled up?

Ans:

When you pull the syringe’s piston up, you’re essentially creating a temporary, miniature vacuum inside the barrel. This vacuum isn’t a force of “sucking,” but rather a dramatic drop in pressure.

Here’s a step-by-step breakdown using a simple analogy:

1. The Starting Point: Before you pull the piston, the air pressure inside the barrel is the same as the atmospheric pressure outside, pushing on the liquid from all directions. The liquid sits still because these forces are balanced.
2. Creating a “Low-Pressure Zone”: As you retract the piston, you rapidly increase the space inside the barrel. The air molecules inside are now spread incredibly thin, trying to fill this new, larger volume. This results in a region of very low pressure inside the syringe.
3. The Power of the Atmosphere: The liquid in the vial or container you’ve inserted the needle into is exposed to the normal, high pressure of the Earth’s atmosphere pushing down on its surface. Nature always seeks balance, striving to equalize pressure differences.
4. The Push from Below: To correct this imbalance, the higher-pressure air outside pushes down on the surface of the liquid in the vial. This force is transmitted through the liquid, driving it up through the needle and into the low-pressure zone of the syringe barrel. The liquid is quite literally pushed up by the weight of the air above it.

A Simple Analogy: Imagine an empty, sealed plastic bottle. If you were to squeeze it, you’d increase the pressure inside and air would rush out if you opened the cap. Now, imagine you could magically expand the bottle without letting any air in. You would create a low-pressure area inside. If you then opened the cap near water, the outside air pressure would immediately push water into the bottle to fill the space and balance the pressure. Pulling a syringe piston does exactly this.

Question 9. 

How is water drawn up from a well by a water pump?

Ans:

How a Hand Pump Draws Water From a Well

Drawing water from a well with a hand pump relies on a clever dance between human effort, mechanical valves, and the invisible force of air pressure. It’s a two-stroke cycle that first creates a vacuum and then uses that vacuum to pull water upward.

The Core Principle: Harnessing a Vacuum

The key player is not the pump sucking the water up, but the weight of our atmosphere pushing the water up. The pump’s job is to remove the air from a sealed pipe, creating a low-pressure area (a partial vacuum) inside. The higher air pressure pushing down on the surface of the water in the well then forces the water up into this empty space. This is the same principle you use when drinking a liquid through a straw; you create a low pressure in your mouth, and the atmospheric pressure does the work of pushing the drink up the straw.

Stage 1: The Upstroke (Creating the Suction)

• Your Action: You pull the handle up.
• Inside the Pump: This raises a piston inside the main cylinder. Attached to this piston is a leather flap or a one-way valve, often called the piston valve.
• Valve Action:
• As the piston moves up, it creates an empty, low-pressure space beneath it.
• This suction causes a lower valve at the very bottom of the pump, submerged in the well water, to open. This is the foot valve (a one-way check valve).
• The higher atmospheric pressure on the well’s water surface now has a path. It forces water up through the open foot valve to fill the void beneath the rising piston.
• Meanwhile, at the Spout: On this upstroke, the piston valve above stays closed, preventing air from being sucked in from the top.

Stage 2: The Downstroke (Setting the Trap and Delivering Water)

• Your Action: You push the handle down.
• Inside the Pump: The piston now moves downward, pressurizing the space below it.
• Valve Action:
  • This downward pressure immediately forces the foot valve at the bottom to snap shut. This traps the column of water that was just drawn up, preventing it from falling back into the well.
  • The trapped water now has only one place to go: it pushes open the piston valve in the middle of the piston itself.
• The Payoff: As you complete the downstroke, the water is forced through the open piston valve and collects in the chamber above the piston. The first few strokes prime the system, but soon, with every downstroke, a volume of water is displaced and pushed out through the spout.

The Continuous Cycle

With each subsequent upstroke, the piston once again lifts, drawing a new batch of water from the well. Simultaneously, it lifts the water that is now sitting on top of it, ready to be poured out. The downstroke continues to push this water toward the spout while drawing the next batch into the lower chamber. This cycle of lift-and-push, governed by the precise timing of the two one-way valves, creates a steady flow of water from the depths of the well to your bucket.

Question 10. 

A partially inflated balloon is placed inside a bell jar connected to a vacuum pump. On creating vacuum inside the bell jar, balloon gets more inflated. How does the pressure change: increase, decrease or remain the same, inside the (a) bell jar, (b) balloon?

Ans:

Analyzing the Pressure Changes in the Bell Jar and Balloon

This is a classic demonstration of how gases behave when the forces acting upon them change. The key to understanding the result lies in the concept of pressure equilibrium and the elastic nature of the balloon.

(a) Pressure Inside the Bell Jar

The pressure inside the bell jar decreases dramatically.

This is the direct and intended outcome of the experiment. A vacuum pump actively removes air molecules from the sealed bell jar. With fewer molecules colliding with the inner walls of the jar, the internal pressure drops significantly, creating a partial vacuum.

(b) Pressure Inside the Balloon

The pressure inside the balloon also decreases, but for a different reason and to a lesser extent.

This part is more nuanced. Initially, the partially inflated balloon is in a state of equilibrium; the air pressure inside the balloon pushing outward is perfectly balanced by the higher atmospheric pressure inside the bell jar pushing inward.

When the vacuum pump removes the surrounding air from the jar, this balancing external pressure is drastically reduced. The stretched rubber of the balloon, which was being compressed by the outside air, now has far less force to push against. Consequently, the elastic skin of the balloon expands outward forcefully.

As the balloon expands, the volume of space inside the balloon increases. The same number of air molecules that were inside the balloon initially must now fill a larger area. This causes the internal pressure to decrease because the molecules are more spread out.

A Simple Analogy:

Imagine you are squeezing a soft, air-filled stress ball in your hand. Your hand represents the normal atmospheric pressure inside the bell jar, compressing the ball. When you suddenly release your grip (akin to creating a vacuum in the jar), the ball expands. The air inside the ball was at a certain pressure when compressed; when the ball expands, that internal pressure drops because the air has more room. The balloon in the experiment behaves in the same way.

Summary:

In short, the pressure drops everywhere, but it’s a chain reaction:

1. The pump actively decreases the pressure in the bell jar.
2. This pressure drop removes the confining force on the balloon, allowing it to expand.
3. The expansion of the balloon causes a decrease in its own internal pressure as the enclosed gas fills a larger volume.

Question 11. 

What is the purpose of a barometer?

Ans:

The primary purpose of a barometer is to measure the weight of the air above us, known as atmospheric pressure. While often simplified as a “weather forecasting” tool, its fundamental role is as a gauge for the invisible force exerted by the Earth’s atmosphere.

Think of the atmosphere not as empty space, but as a deep, invisible ocean. We live at the bottom of this ocean of air, and it has a significant weight. A barometer is the device that measures the “pressure” at this bottom, which constantly changes.

This measurement serves several critical purposes:

1. The Classic Use: Weather Prediction
This is the most well-known application. Changes in air pressure are a powerful indicator of short-term weather shifts.

• Falling Pressure: When the barometric reading drops, it signals that the column of air above you is becoming lighter. This typically happens as a mass of less-dense, warm, moist air moves in, often preceding clouds, rain, or storms. It’s nature’s way of signaling that unsettled weather is likely approaching.
• Rising Pressure: An increase in the reading means a heavier, denser mass of cool, dry air is settling in. This is a reliable predictor of stable, clear, and fair weather conditions.

In essence, it doesn’t just describe the current weather, but acts as a prophet of the weather to come, allowing farmers, sailors, and anyone outdoors to make informed decisions.

2. A Vital Tool for Navigation and Altitude

• For Pilots and Hikers: A barometer is the core of an altimeter. Since air pressure decreases predictably with altitude, the device can be calibrated to show how high you are above sea level rather than just the pressure. For a pilot in the clouds or a hiker on a mountain trail, it provides a crucial vertical reference point.
• For Mariners: At sea level, barometers are essential for anticipating major storms and squalls, providing a critical early warning long before the skies darken.

3. A Scientific and Environmental Benchmark
Beyond daily forecasts, barometers are indispensable for:

• Scientific Research: They are used to track long-term climate patterns and study the dynamics of the atmosphere.
• Industrial Applications: In various industries, precise pressure measurements are necessary for processes that are sensitive to environmental conditions.

Question 12. 

1 .What is a barometer? 

2. How is a simple barometer constructed?

Ans:

1. What is a Barometer?

A barometer is essentially a weather forecasting instrument that measures the weight of the air above us, known as atmospheric pressure. Think of the atmosphere as a vast, invisible ocean of air that exerts a constant push on everything it touches. A barometer acts as a gauge for this push.

Just as a swimmer feels more pressure the deeper they go, the air at sea level is “deeper” in the atmosphere and experiences higher pressure than air on a mountaintop. Weather systems bring changes in this pressure; a mass of dense, cool air increases pressure (often meaning fair weather), while a mass of warm, moist air is less dense and decreases pressure (often signaling storms). By tracking these changes, a barometer helps predict short-term shifts in the weather.

2. Constructing a Simple Mercury Barometer

While modern digital barometers exist, the classic mercury barometer powerfully demonstrates the principle. Here’s how one can be built, following the pioneering experiment of Evangelista Torricelli in 1643.

The Required Materials:
You would need a long, glass tube—about one meter in length—sealed at one end, a small bowl (often called the cistern), and a sufficient quantity of mercury, a very dense liquid metal.

The Step-by-Step Process:

1. Filling the Tube: The sealed glass tube is completely filled with mercury. It is essential to ensure there are no air bubbles trapped inside, as they would compromise the instrument’s accuracy.
2. The Inversion: Wearing protective gear due to mercury’s toxicity, you carefully place a finger over the open end of the tube and invert it. While keeping the end sealed by your finger, you lower it into the bowl, which is also partially filled with mercury.
3. The Crucial Moment: You then remove your finger from the open end while it remains submerged in the mercury in the bowl. At this point, a portion of the mercury in the tube will flow out into the bowl.
4. Observing the Equilibrium: However, the mercury does not empty completely. A column of mercury, approximately 76 centimeters (or 760 millimeters) tall at sea level, remains standing in the tube. The space above the mercury in the sealed top of the tube is a vacuum, known as a “Torricellian vacuum.”

The Science Behind It:
The column of mercury is held up not by suction, but by the sheer force of the outside air pressing down on the surface of the mercury in the bowl. This atmospheric pressure pushes the mercury up the tube until its weight perfectly balances the pressure from the air. It is a continuous tug-of-war between the weight of the mercury column and the weight of the air column above the bowl. When atmospheric pressure rises, it pushes more mercury into the tube, causing the column to rise. When pressure falls, the mercury column drops accordingly. The height of this mercury column is a direct measure of the atmospheric pressure at that time and location.

Question 13. 

Explain how the height of mercury column in tube of a simple barometer, a measure of the atmospheric pressure.

Ans:

Imagine a strong, glass tube, sealed tightly at one end like a long straw with a plugged top. This tube is first completely filled with the liquid metal, mercury. It is then swiftly inverted and placed upright into a small, open dish that is also filled with mercury.

Once inverted, the mercury inside the tube does not simply empty out. Instead, it drops down only partway, leaving an empty space at the sealed top of the tube. This space is a vacuum—a region devoid of any air or substance. The column of mercury stops its descent and settles at a specific, measurable height.

The force preventing the entire column from draining out is the weight of the Earth’s atmosphere pressing down on the surface of the mercury in the open dish. The atmosphere is a deep ocean of air, and it exerts pressure on everything it touches. In this setup, it pushes down on the mercury in the dish, which in turn pushes mercury up into the tube.

The system reaches a perfect standstill. The downward push of the atmosphere on the dish is precisely balanced by the upward push of the mercury column’s own weight inside the tube. The mercury column acts as a precise weighing scale for the air itself.

Therefore, the height of this mercury column becomes a direct and accurate measure of the atmospheric pressure pushing on the dish. If the atmospheric pressure increases, it pushes harder on the dish mercury, forcing the column in the tube to rise to a greater height to balance the increased weight. Conversely, if the atmospheric pressure drops, the push weakens, and the column falls to a lower height as its weight now exceeds the supporting force from the atmosphere.

The choice of mercury is crucial. It is an exceptionally dense liquid, so a column only about 76 centimeters (30 inches) tall is needed to balance the atmosphere. A similar barometer using water would require a tube over 10 meters long, making it highly impractical. The mercury barometer elegantly translates the invisible force of air pressure into a clear, visible measurement of height.

Question 14.

Illustrate with the help of a labelled diagram of a simple barometer that the atmospheric pressure at a place is 76 cm of Hg.

Ans:

Demonstrating Atmospheric Pressure with a Mercury Barometer

The following illustration and description explain how a simple mercury barometer measures atmospheric pressure, demonstrating why it is equated to 76 cm of mercury (Hg).

Diagram Description:

Imagine a simple setup with the following labelled parts:

1. A Long Glass Tube: About 1 meter in length, sealed at one end. It is completely filled with pure mercury (Hg), with no air bubbles inside.
2. A Mercury Reservoir: An open dish partially filled with mercury.
3. The Inverted Tube: The mercury-filled tube is carefully inverted, and its open end is placed below the surface of the mercury in the reservoir.
4. The Mercury Column: Once inverted, the mercury in the tube descends a little, but stops, leaving an empty space at the top of the sealed tube. This space is a vacuum, known as the Torricellian Vacuum.
5. A Vertical Scale: A measuring scale is placed next to the tube, with its zero point aligned with the surface of the mercury in the reservoir.

The diagram shows the mercury level inside the tube has stabilized at a height ‘h’ above the reservoir level. The label points to this height, h = 76 cm.

Explanation of the 76 cm Hg Measurement

The functioning of this barometer is a classic demonstration of a balance of pressures.

When the mercury-filled tube is inverted into the reservoir, the column of mercury inside the tube begins to fall. It does not fall completely because the pressure of the outside air acting on the open surface of the mercury in the reservoir is pushing against it.

The mercury column stops falling at the precise point where the pressure it exerts downwards is exactly balanced by the pressure exerted upwards by the Earth’s atmosphere.

• The downward pressure is due to the weight of the mercury column itself. It is calculated as the product of the height of the column (‘h’), the density of mercury (ρ), and gravitational acceleration (g).
• The upward pressure is the Atmospheric Pressure acting on the reservoir’s surface.

This creates an equilibrium:

Pressure due to Mercury Column = Atmospheric Pressure

If the height ‘h’ of the mercury column is measured to be 76 centimeters, it means the atmospheric pressure at that place and time is exactly sufficient to support a column of mercury 76 cm tall.

Therefore, we state that the atmospheric pressure is “76 cm of Hg”. This is a unit of pressure, meaning the pressure is equivalent to the pressure at the base of a 76-centimeter-high column of mercury. At sea level under standard conditions, this height averages around 76 cm, which is also defined as one standard atmosphere (1 atm) of pressure.

Question 15. 

Why is the barometric height used as a unit to express the atmospheric pressure?

Ans:

The use of barometric height (like millimeters of mercury) as a unit for atmospheric pressure is a historical legacy born from a fundamental and visually intuitive experiment. It persists because it provides a tangible, concrete way to conceptualize an otherwise invisible force.

The story begins with Evangelista Torricelli’s famous experiment in 1643. He filled a long glass tube with mercury and inverted it into a dish of mercury. The column of mercury did not drain out completely; instead, it dropped to a specific height and stabilized. Torricelli brilliantly reasoned that the vacuum at the top of the tube offered no support to the mercury column. The only thing preventing the rest of the liquid metal from falling was the weight of the outside air pressing down on the surface of the mercury in the dish.

This created a perfect balance: the pressure exerted by the atmosphere on the dish was exactly equal to the pressure exerted by the weight of the mercury column in the tube. Therefore, the height of the column became a direct physical measure of the atmospheric pressure. If the air pressure increased, it pushed harder on the dish and forced the mercury column higher. If the pressure dropped, the column fell to a lower height.

This is why the unit became so deeply ingrained. Scientists could literally read the air pressure by observing a scale on their apparatus. It transformed an abstract force into a simple linear measurement. Saying “the pressure is 760 mmHg” was not just a number; it was a description of an experimental setup. It meant: “The current atmospheric pressure is sufficient to support a column of mercury 760 millimeters tall.”

This system had profound practical advantages. A mercury barometer is a self-contained, primary standard. It doesn’t require calibration against another device; its operation is defined by the fundamental properties of gravity and fluid density. This made it an incredibly reliable and reproducible standard for centuries, allowing scientists and meteorologists across the globe to compare measurements accurately.

While modern SI units like Pascals are more fundamental (being a direct measure of force per area), the older units like mmHg, and the related torr (1 torr ≈ 1 mmHg), remain in use, particularly in medicine for blood pressure and in meteorology. They endure as a direct link to the elegant physical experiment that first gave us the ability to weigh the air, turning a column of liquid in a glass tube into a universal ruler for the atmosphere itself.

Question 16. 

What is meant by the statement ‘the atmospheric pressure at a place is 76 cm of Hg’? State its value in Pa.

Ans:

The statement “the atmospheric pressure at a place is 76 cm of Hg” is a historical and practical way of expressing the weight of the air above us. It means that at that specific location, the pressure exerted by the entire column of Earth’s atmosphere is strong enough to support a column of liquid mercury (Hg) that is 76 centimeters tall in a device called a mercury barometer.

In simpler terms, the air is pushing down with a force that can hold up a 76 cm tall “stick” of mercury in a sealed, inverted tube. If the atmospheric pressure increases, it can push the mercury higher, say to 77 cm. If the pressure decreases, the mercury column will drop to a lower height, like 75 cm.

This measurement is based on a classic experiment. A long glass tube, filled with mercury and then inverted into a dish of mercury, will have an empty space at the top (a vacuum) and the mercury level in the tube will drop and stabilize at a specific height. This height is a direct measure of the outside air pressure.

Its Value in Pascals (Pa)

To convert this value to the modern SI unit of Pascals, we calculate the pressure exerted by that specific column of mercury.

Where:

• h is the height of the liquid column = 0.76 m
• ρ is the density of mercury = 13,600 kg/m³
• g is the acceleration due to gravity = 9.8 m/s²

Let’s calculate:
P = (0.76 m) × (13,600 kg/m³) × (9.8 m/s²)
P = 101,292.8 Pa

This is typically rounded to 101,293 Pa or, more commonly, 1.01 × 10⁵ Pa.

This value is often referred to as one standard atmosphere (1 atm), and it represents the average atmospheric pressure at sea level.

Question 17. 

How will you show that there is vacuum above the surface of mercury in a barometer? What name is given to this vacuum?

Ans:

To demonstrate the existence of a vacuum above the mercury in a barometer, you can perform a simple yet revealing experimental test.

The Demonstration:

First, prepare a traditional mercury barometer, which consists of a long glass tube, sealed at one end, filled with mercury and inverted into a dish of mercury. The mercury column will fall until it is approximately 76 cm high, leaving an empty space at the sealed top.

Now, for the key part: carefully tilt the barometer tube. As you incline it, observe the behavior of the mercury inside. You will notice that while the length of the mercury column within the tube increases as it angles towards the horizontal, its vertical height from the surface of the mercury in the dish to the top of the column remains constant. Crucially, the mercury never completely fills the tube; the space at the top is preserved.

The Proof and Reasoning:

This observation is the critical proof. If any air were present in that space, it would be a compressible gas. When you tilt the tube, the mercury would compress this trapped air as it occupies more of the tube’s length, causing the vertical height to decrease. The fact that the vertical height remains unchanged demonstrates that there is no air present to compress. The space offers no resistance and is therefore a void—a vacuum.

An everyday analogy is drinking from a straw. When you suck, you remove air, creating a partial vacuum, and the liquid rises. If you sealed the top of a long straw full of liquid and lifted it, the liquid would fall, leaving a vacuum at the top, just like in the barometer tube.

The Name of the Vacuum:

This empty space is scientifically known as the Torricellian Vacuum, named after Evangelista Torricelli, the Italian physicist who invented the mercury barometer in 1643. The vacuum is not “perfect,” as it contains a tiny amount of mercury vapor, but for all practical purposes, it is considered a vacuum and is entirely free of air.

Question 18. 

1. How is the barometric height of a simple barometer affected if  Its tube is pushed down into the trough of mercury?

2. How is the barometric height of a simple barometer affected if  Its tube is slightly tilted from vertical?

3. How is the barometric height of a simple barometer affected if A drop of liquid is inserted inside the tube?

Ans:

1. How is the barometric height affected if its tube is pushed down into the trough of mercury?

The barometric height, which is the vertical distance from the free surface of the mercury in the trough to the top of the mercury column inside the tube, remains completely unchanged.

Pushing the tube deeper into the trough only changes the tube’s position, not the fundamental physics at play. The mercury column is supported solely by the atmospheric pressure pushing down on the reservoir’s surface. This external pressure balances the weight of the mercury column, and the height of that column is what defines the barometric reading. As long as the top of the tube remains above the mercury level equivalent to atmospheric pressure (about 76 cm), submerging the tube further simply raises the level of mercury inside the trough, leaving the crucial vertical height of the suspended column the same.

• Simple Analogy: Imagine you have a ruler standing in a pool. Marking the water level on the ruler. Pushing the ruler deeper into the pool changes the ruler’s position, but the water level mark on the ruler itself doesn’t change. The barometric height is like that fixed mark.

2. How is the barometric height affected if its tube is slightly tilted from vertical?

The barometric height, correctly defined as the vertical height of the mercury column, remains unaffected. However, the length of the mercury column observed along the tilted tube will be longer.

When you tilt the tube, the mercury must still exert the same pressure downward to balance the atmosphere. Pressure depends on vertical height, not the length of the fluid along a slope. The mercury will adjust its position, creating a longer diagonal column whose vertical projection matches the original, correct barometric height. To get an accurate reading, you must measure the vertical distance from the meniscus in the tube down to the trough’s mercury level, not the distance along the tube.

• Simple Analogy: Think of a right-angled triangle. The tilted tube is the hypotenuse (longest side), but the vertical height of the triangle (the side opposite the right angle) stays constant. Tilting the tube increases the hypotenuse length while the vertical height remains the same.

3. How is the barometric height affected if a drop of liquid is inserted inside the tube?

The barometric height will decrease, showing a false, lower reading of atmospheric pressure.

This occurs because the introduced liquid, say water, will vaporize into the vacuum (Torricellian vacuum) at the top of the tube. This vapor exerts its own pressure downwards on the mercury column. Now, the mercury column is no longer balanced solely by the atmospheric pressure from outside. It is balanced by the atmospheric pressure minus the pressure of the vapor inside. To achieve this new, lower equilibrium, the mercury column drops to a shorter vertical height. The space at the top is no longer a vacuum but contains vapor at a low pressure.

• Simple Analogy: It’s like if someone was pushing up on the other side of a seesaw to help you lift a weight. With help, you don’t have to push down as hard. The vapor pressure is “helping” the atmosphere push down on the mercury column, so the column doesn’t need to be as heavy (tall) to balance the seesaw.

Question 19. 

State two uses of a barometer.

Ans:

1. Calibrating Altitude for Aviation Safety: In aviation, a barometer is integral to the altimeter, which tells a pilot how high the aircraft is flying. However, as atmospheric pressure changes with weather, the altimeter reading can become inaccurate. Pilots use barometric pressure reports from ground stations to manually calibrate their altimeters. This ensures that all aircraft in a given airspace are operating with the same, precise altitude reference, preventing collisions and ensuring a safe vertical separation between planes.

2. Managing Environmental Conditions in Scientific Cultivation: For scientists growing sensitive materials like crystalline structures or specific biological cultures in laboratories, even minor shifts in air pressure can disrupt the process. A barometer is used to continuously monitor the pressure within a sealed growth chamber or glove box. If the pressure deviates from the required set point, it triggers adjustments to the environmental control systems, preserving the integrity of the delicate experiment or culture.

Question 20. 

Give two reasons for use of mercury as a barometric liquid.

Ans:

Mercury is chosen as the barometric liquid primarily due to its unique physical properties, which are ideally suited for measuring atmospheric pressure.

1. Its High Density Enables a Manageable Instrument Size.
Mercury is approximately 13.6 times denser than water. Since the height of the liquid column in a barometer is inversely proportional to its density, mercury only needs to rise about 760 mm to balance average atmospheric pressure. A water-based barometer, in contrast, would require a tube over 10 meters tall, making it impractical for standard use. Mercury’s high density allows for the construction of a compact and conveniently sized instrument.

2. Its Negligible Vapor Pressure Ensures a Stable Vacuum.
At ordinary temperatures, mercury has an extremely low vapor pressure, meaning it barely evaporates. This is critical for maintaining the Torricellian vacuum—the empty space above the liquid column in the sealed tube. If a liquid with high vapor pressure were used, molecules would evaporate and fill this space with vapor, exerting its own downward pressure. This would depress the liquid column and lead to an inaccurate, unstable reading. Mercury’s low vapor pressure preserves a near-perfect vacuum, ensuring consistent and reliable measurements.

Question 21. 

Give two reasons why water is not a suitable barometric liquid.

Ans:

1. Exceptionally Low Density

Water has a relatively low density compared to traditional barometric liquids like mercury. Because a barometer balances the weight of the liquid column against atmospheric pressure, a less dense liquid must rise much higher to achieve this balance. For instance, to measure standard atmospheric pressure, a water barometer would require a column over 10 meters (34 feet) tall, whereas a mercury column is only about 0.76 meters (30 inches) high. This makes a water-based barometer impractically tall for any standard use and extremely difficult to transport, set up, or read accurately in a typical setting.

2. High Vapor Pressure and Evaporation

Water evaporates readily at normal temperatures, creating significant water vapor (a gas) in the space above the liquid column in the tube, known as the Torricellian vacuum. This vapor exerts its own pressure, which pushes down on the water column. This additional force means the column does not fall as low as it should based on atmospheric pressure alone, leading to consistently inaccurate and falsely high readings. Furthermore, this evaporation can be exacerbated by temperature changes, introducing another variable that makes the device unreliable. In contrast, mercury has a negligible vapor pressure at room temperature, so the space above it remains a near-perfect vacuum, which is essential for an accurate measurement.

Question 22. 

Mention two demerits of a simple barometer and state how they are removed in a Fortin barometer .

Ans:

Demerit 1: The Variable Level of the Mercury in the Cistern

In a simple barometer, the open cistern of mercury is directly exposed. When atmospheric pressure increases, it pushes more mercury from the cistern into the glass tube, causing the level in the cistern to fall. Conversely, when pressure decreases, mercury flows back from the tube into the cistern, causing the cistern level to rise.

This creates a significant problem: the zero point of the scale (the level of the mercury in the cistern) is constantly shifting. To get an accurate reading of the height of the mercury column, you must measure from the current, variable surface in the cistern, which is impractical and leads to error.

How the Fortin Barometer Removes This:
The Fortin barometer features a flexible, leather-based cistern at its bottom. The level of the mercury in this cistern can be manually adjusted using a thumbscrew. Before taking a reading, the user turns this screw to force the mercury surface upwards until it just makes contact with a fixed ivory pointer. This ivory pin acts as a permanent, invariable zero mark. By ensuring the mercury always touches this point at the start of a measurement, the Fortin barometer guarantees that every reading is taken from a consistent and known reference level, eliminating the error caused by a shifting zero point.

Demerit 2: Parallax Error in Reading the Mercury Column

In a simple barometer, taking a precise reading of the mercury’s height against a fixed scale is tricky. If your eye is not perfectly level with the top of the mercury meniscus, you will introduce a “parallax error,” where the reading appears higher or lower than it actually is. This is a common source of inaccuracy.

How the Fortin Barometer Removes This:
The Fortin barometer is equipped with a vernier scale that slides alongside the main scale. This vernier scale allows for measurements to be taken with much greater precision (typically down to 0.1 mm). Crucially, the barometer has a metal collar with a horizontal slit that can be moved up and down. To take a reading, the user adjusts this collar until its bottom edge appears to be in perfect, straight alignment with the top of the mercury meniscus. This ingenious method ensures the user’s line of sight is always exactly horizontal to the mercury, completely eliminating parallax error and enabling a highly accurate and repeatable measurement.

Question 23. 

Draw a simple labelled diagram of a Fortin barometer and state how it is used to measure the atmospheric pressure.

Ans: 

A Simple Labelled Diagram of a Fortin Barometer

Unfortunately, I cannot physically draw a diagram here. However, I can provide you with a detailed, text-based description that you can easily use to create your own accurate sketch.

Imagine a diagram with the following labels on a glass tube inverted in a mercury reservoir:

1. Main Scale: A vertical scale, typically in millimeters or inches, fixed to the top of the instrument’s case.
2. Vernier Scale: A movable scale attached to the slider, used for taking highly precise readings.
3. Glass Tube: A long, glass tube filled with mercury, inverted at the bottom.
4. Mercury Reservoir: A leather-based container at the bottom holding a supply of mercury.
5. Ivory Pointer: A fixed, sharp ivory point at the top of the reservoir. Its tip is the “zero” of the main scale.
6. Adjusting Screw: A screw at the bottom of the reservoir used to raise or lower the mercury level.
7. Slider with Vernier: A movable part that holds the vernier scale and is adjusted to align with the top of the mercury column.

How a Fortin Barometer is Used to Measure Atmospheric Pressure

The key principle of the Fortin barometer is that atmospheric pressure supports a column of mercury in a vacuum. The height of this column is a direct measure of the atmospheric pressure. The unique feature of the Fortin barometer is its adjustable reservoir, which ensures a consistent starting point for every measurement.

Here is the step-by-step process:

Step 1: Setting the Zero Point
Before reading the height of the mercury, you must first ensure the mercury in the reservoir is exactly at the zero point.

• Look at the ivory pointer. Its sharp tip is the reference point.
• Gently turn the adjusting screw at the bottom. This moves the leather base of the reservoir up or down, causing the mercury level to rise or fall.
• Adjust until the surface of the mercury in the reservoir just touches the tip of the ivory pointer. You will see its reflection perfectly meet the tip itself when viewed at eye level. This sets the “zero” for the measurement.

Step 2: Taking the Reading
With the zero point correctly set:

• Move the slider that holds the vernier scale.
• Carefully adjust it so that the bottom edge of the vernier scale is perfectly aligned with the meniscus (the curved top surface) of the mercury column in the glass tube. Ensure your eye is at the same level to avoid parallax error.

Step 3: Reading the Scales
The pressure is read from the two scales:

• Read the value from the main scale where the zero line of the vernier scale aligns.
• Then, look along the vernier scale to find the line that exactly matches a line on the main scale. This gives you the fractional part of the reading.

The final value (e.g., 758.4 mm of Hg) is the precise atmospheric pressure at that moment. This entire process of adjusting the reservoir and using the vernier scale is what makes the Fortin barometer exceptionally accurate for scientific work.

Question  24. 

What is an aneroid barometer? Draw a neat and labelled diagram to explain its construction and working.

Ans:

What is an Aneroid Barometer?

An aneroid barometer is a scientific instrument used to measure atmospheric pressure without using any liquid, unlike its predecessor, the mercury barometer. The word “aneroid” itself comes from the Greek words meaning “without liquid.” It is a vital tool in weather forecasting, as changes in atmospheric pressure are a primary indicator of short-term weather changes. For instance, falling pressure typically suggests stormy or rainy weather is approaching, while rising pressure indicates fair, stable conditions.

Its compact, portable, and safe design (no risk of mercury spills) makes it far more practical for everyday use in homes, boats, and aircraft.

Construction of an Aneroid Barometer

The construction is ingenious, relying on mechanical parts to detect subtle changes in air pressure. Its main components are:

1. Airtight Metal Chamber (Capsule): This is the heart of the instrument. It is a small, flexible, sealed box made of thin, corrugated metal (often beryllium copper or a similar alloy). Most of the air has been removed from inside this box, creating a partial vacuum.
2. Strong Spring: To prevent the external air pressure from completely crushing the flexible box, a strong internal or external spring is attached. This spring provides counter-pressure, allowing the box to flex slightly in and out.
3. Lever System (Linkage): A series of tiny, hinged levers is connected to the surface of the metal chamber. This system acts as an amplifier. The minuscule expansion and contraction of the chamber are greatly magnified by this linkage.
4. Chain or Link: The final lever in the system is connected to a fine chain.
5. Spindle and Pointer: The chain is wrapped around a spindle (axle). As the chain is pulled or released by the lever system, the spindle rotates. A pointer or needle is attached to this spindle.
6. Calibrated Dial: The pointer moves over a circular dial that is marked with pressure units (such as inches of mercury or millibars/hectopascals) and often with general weather terms like “Rain,” “Change,” “Fair,” and “Very Dry.”
7. Display Glass and Case: The entire mechanism is housed within a protective case with a glass front to allow for easy reading while keeping the delicate parts safe.

Working Principle

The working of the aneroid barometer is based on a simple physical principle: the flexible, evacuated chamber changes its shape in response to changes in the external atmospheric pressure.

Here is a step-by-step breakdown of the process:

• When Atmospheric Pressure INCREASES:
  1. The higher pressure outside presses down on the flexible metal chamber.
  2. The chamber compresses or contracts slightly.
  3. This small inward movement is captured and amplified by the lever system.
  4. The levers pull on the chain, which turns the spindle.
  5. The spindle rotates the pointer clockwise on the dial, indicating a rise in pressure.
• When Atmospheric Pressure DECREASES:
  1. The reduced pressure outside exerts less force on the metal chamber.
  2. The internal spring, now stronger than the external pressure, causes the chamber to expand outward.
  3. This small outward movement is amplified by the lever system in the opposite direction.
  4. The chain is released, allowing the spindle to rotate the pointer counter-clockwise on the dial, indicating a fall in pressure.

By observing the direction and magnitude of the pointer’s movement, one can predict impending weather changes. A rapid fall in the needle is a reliable sign of an approaching storm system.

Labelled Diagram (Explanation for Drawing)

To draw a neat and labelled diagram, you can sketch the following components based on the description above. A cross-sectional view is most effective.

(Imagine a detailed, hand-drawn diagram here)

Labels for Your Diagram:

1. Flexible, Evacuated Metal Chamber: Draw a wavy, corrugated box in the center.
2. Strong Spring: Show a spring inside or attached to the chamber.
3. Lever System (Linkage): Draw a series of connected, hinged arms touching the top of the chamber.
4. Chain: Show a fine chain connecting the end of the lever to a spindle.
5. Spindle: Draw a small axle with the chain wrapped around it.
6. Pointer (Needle): Attach a long needle to the spindle.
7. Calibrated Dial: Draw the semi-circular dial behind the pointer with markings for pressure and weather.
8. Case: Draw the outer casing enclosing the entire mechanism.

This combination of a clear explanation and a guided description for a diagram provides a complete understanding of the aneroid barometer’s construction and working, created to be a unique resource.

Question  25. 

State two advantages of an aneroid barometer over a simple barometer.

Ans:

1. Enhanced Portability and Durability: Unlike the simple barometer which relies on a fragile glass tube and a column of liquid, the aneroid barometer uses a small, flexible metal box. This solid-state design makes it inherently more robust, resistant to spills and breakage, and compact enough to be mounted on a wall or carried for field use, which is impossible with a cumbersome, liquid-filled tube.
2. Improved Safety and Practical Installation: The simple barometer contains a significant amount of toxic mercury, posing a health hazard and a difficult cleanup if the tube is broken. The aneroid barometer eliminates this danger entirely. Furthermore, its compact and sealed mechanism allows it to be easily installed anywhere, such as in an aircraft cockpit or a boat, without concern for liquid sloshing or tube orientation.

Question  26. 

How is the reading of a barometer affected when it is taken to (i) a mine, and (ii) a hill?

Ans:

A barometer measures atmospheric pressure, which is the weight of the air column above it. Changes in altitude directly affect this reading.

(i) Taken to a Mine:

When a barometer is taken deep into a mine, its reading increases.

This happens because the instrument is descending further below the Earth’s surface. While we often think of altitude starting at sea level and going up, a mine takes you to a negative altitude. At the bottom of a mine, the barometer is now underneath a greater portion of the atmosphere. It has the entire column of air from the mine’s entrance down to its current depth added to the normal atmospheric column above the entrance. This extra weight of air results in a higher barometric pressure reading.

In simple terms, the deeper you go into a mine, the more air you have above you, so the pressure goes up, similar to how water pressure increases the deeper you swim.

(ii) Taken to a Hill:

When a barometer is taken to the top of a hill, its reading decreases.

This is the more commonly understood effect. As you ascend a hill, you are moving to a higher altitude. At this elevated point, there is less atmosphere above the barometer pressing down on it. The column of air extending from the hilltop up to the edge of space is shorter and therefore lighter than the column of air from sea level upwards. With less weight of air above it, the barometer registers a drop in atmospheric pressure.

Question 27. 

How does the atmospheric pressure change with altitude? Draw an approximate graph to show this variation.

Ans:

How Atmospheric Pressure Changes with Altitude

The air around us has weight, and atmospheric pressure is the force exerted by the weight of this air column above a given point. As you go higher in altitude, there is less air above you pushing down. Therefore, atmospheric pressure decreases as altitude increases.

This decrease isn’t a simple, straight-line relationship. It’s non-linear and exponential, meaning the pressure drops very rapidly at first and then more slowly at higher altitudes. Here’s why:

1. Gravity’s Pull: Gravity pulls the air molecules closer to the Earth’s surface, making the air denser at lower levels. 
2. Compressibility of Air: Because air is compressible, the dense air at sea level is “squashed” by the air above it. As you ascend, this compression lessens, leading to a rapid drop in density and pressure.
3. The 50% Rule: A handy rule of thumb is that approximately 50% of the total mass of the atmosphere lies below an altitude of about 5.5 kilometers (18,000 feet or 3.4 miles). This shows just how quickly the pressure falls off in the first few kilometers.

Approximate Graph of Pressure vs. Altitude

Below is a simple text-based graph that illustrates this exponential decay.

text

Atmospheric Pressure (kPa)

^

|                                                                   *

|                                                          *

|                                                  *

|                                          *

|                                   *

|                            *

|                     *

|              *

|         *

|    *

+—————————————————————–> Altitude (km)

0    5    10   15   20   25   30

(Sea Level)

Key Takeaways from the Graph:

• Steep Drop at Low Altitudes: The line is steepest near sea level (0 km). The pressure plummets as you leave the surface. For example, at around 5.5 km, pressure is roughly half of what it is at sea level.
• Gradual Decline at High Altitudes: As the altitude increases beyond 10-15 km, the curve flattens out. The pressure continues to decrease, but it takes a much larger change in altitude to see a significant drop in pressure because the air is already so thin.
• Never Reaches Zero: In theory, the line would get closer and closer to zero pressure but never quite touch it, extending far into outer space.

Question  28. 

State two factors which affect the atmospheric pressure as we go up.

Ans:

1. Decrease in the Weight of the Overlying Air: Atmospheric pressure at any point is caused by the weight of the column of air above it. As you ascend to a higher altitude, the height of this air column above you decreases. With less air above pushing down, the weight and therefore the pressure decreases.
2. Decrease in Air Density: The air near the Earth’s surface is compressed by the air above it, making it denser (more air molecules in a given volume). As you go higher, this compression lessens significantly. The air molecules are more spread out, resulting in lower density. Since fewer air molecules are present in a given space to collide and exert force, the atmospheric pressure drops.

Question  29. 

Why does a fountain pen leak at high altitude?

Ans:

The Sky-High Ink Blob: Why Your Fountain Pen Misbehaves in the Clouds

If you’ve ever unscrewed the cap of your fountain pen on an airplane or after a mountain hike to find a messy blob of ink, you’ve experienced a classic phenomenon of physics in action. The culprit isn’t a faulty pen, but the fundamental relationship between air pressure and the delicate, air-based mechanism that makes a fountain pen work.

To understand this, let’s first look at how a fountain pen is designed to function at ground level.

The Delicate Balance at Sea Level

A fountain pen isn’t just a reservoir of ink with a nib. It’s a carefully balanced system that relies on air pressure. Inside the pen’s ink reservoir—whether it’s a cartridge, converter, or built-in sac—there is both ink and a small amount of air.

The ink flows out through the nib via a combination of gravity and capillary action (the same force that draws water up a paper towel). However, for the ink to flow steadily, air must enter the reservoir to replace the volume of ink that has left. This prevents a vacuum from forming that would stop the flow entirely. This air exchange happens through a tiny, cleverly designed breather hole in the nib or through the feed’s intricate channels.

At sea level, the air pressure inside the pen is equal to the air pressure outside the pen. This equilibrium means air enters at the same rate that ink leaves, maintaining a perfect, leak-free balance.

The High-Altitude Upheaval

When you ascend to a high altitude—like in the cabin of a plane flying at 35,000 feet or on a high mountain pass—the external environment changes dramatically.

1. The Squeeze in the Sky: The air inside your pen was trapped at a higher pressure on the ground. As you climb, the atmospheric pressure outside the pen drops significantly. The air inside the pen, however, is still at that higher, ground-level pressure.
2. Expanding Air: This trapped, higher-pressure air needs to expand to equalize with the new, lower-pressure environment. It pushes outward in all directions.
3. The Path of Least Resistance: The solid walls of the cartridge or converter are too strong to expand, and the opening at the back is sealed. The only available path for this expanding air to escape is the same one the ink uses: out through the nib and feed.
4. Forcing the Ink Out: As this bubble of high-pressure air expands and pushes its way through the feed, it doesn’t travel alone. It forcibly pushes a slug of ink ahead of it. The result is that when you uncap the pen, you find an ink-filled cap, a saturated nib, and a potential mess. The pen is essentially “burping” out the excess pressure in the form of ink.

Simple Analogies

• Think of a Shaken Soda Bottle: The carbon dioxide is dissolved in the liquid under pressure. When you open it, the pressure release allows the gas to expand rapidly, pushing the liquid out with it. Your pen experiences a similar pressure release at altitude.
• A Balloon in a Plane: If you blow up a balloon a little bit on the ground and take it on a plane, it will expand as you climb. The air inside is pushing out harder than the thinner air outside is pushing in.

How to Prevent It

The key is to manage this pressure differential.

• Keep it Full: A pen that is completely full of ink has very little air inside to expand. This is the most effective prevention.
• Store it Nib-Up: During ascent, store the pen upright in a shirt pocket or bag. This ensures the expanding air at the top of the reservoir can escape without having to push through a column of ink.
• Let it Adjust: Before you use it at your final altitude, keep the pen nib-up for a little while to allow the internal and external pressures to equalize gradually.

Question  30. 

Why does my nose start bleeding on high mountains?
Ans:

That sudden, surprising trickle of blood from your nose on a mountain hike is a direct result of your body struggling to adapt to a new and challenging environment. It’s not a sign of a major problem, but rather a physical protest from the delicate tissues inside your nose. The main culprits are a combination of pressure, dryness, and your body’s own survival mechanisms.

1. The Squeeze of Thinning Air (The Pressure Problem)

As you climb higher, the atmosphere becomes thinner. There is literally less air pushing down on you, meaning the air pressure drops significantly. However, the pressure inside your body, including the blood vessels in your head and sinuses, remains relatively higher.

Think of it like a sealed plastic bottle at sea level. If you take it up a mountain, the bottle might bulge a little because the pressure inside is now greater than the pressure outside. A similar thing happens in the air-filled spaces in your head. This pressure difference creates a subtle but constant strain on the tiny, delicate capillaries in your nasal passages. They are under stress from the inside, making them more fragile and prone to rupturing.

2. The Desert in the Sky (The Dryness Problem)

Cold mountain air is notoriously dry. As you breathe in, your nose has the important job of warming and humidifying that air before it reaches your sensitive lungs. To do this, it pulls moisture from the rich network of blood vessels lining the nasal passages.

At high altitude, you are often breathing harder and faster due to exertion, forcing a greater volume of this parched air through your nose. This acts like a powerful, continuous drying agent. The mucous membranes in your nose become dehydrated, cracked, and irritated—much like chapped lips. Once these tissues are dry and cracked, the underlying capillaries are exposed and can break open with something as simple as a vigorous breath, a rub of the nose, or even a strong sneeze.

3. Your Body’s High-Altitude Overdrive (The Blood Flow Problem)

To cope with the reduced oxygen at high altitude, your body goes into overdrive. Your heart pumps faster, and your blood pressure can increase slightly to deliver precious oxygen more efficiently. Furthermore, the body naturally directs more blood flow to your core and brain.

The blood vessels in your head and nose, including those fragile capillaries, experience this increased pressure and blood volume. This “high-flow state” is the final push that can cause a already-stressed and dried-out capillary to give way and leak blood.

In a Nutshell:

The nosebleed is a perfect storm. The drop in outside air pressure strains the blood vessels from the inside. The extremely dry air desiccates and cracks the protective nasal lining. Finally, your body’s own increased blood pressure and flow to the area provides the final nudge, causing a fragile vessel to rupture.

How to Help Prevent It:

• Hydrate Constantly: Drink plenty of water before and during your climb. This keeps your entire body, including your nasal tissues, hydrated.
• Use a Saline Spray: Regularly misting your nostrils with a simple saline spray helps to manually add moisture and counteract the drying effect of the air.
• Create Moisture: Breathing through a loosely-woven scarf or a buff can help trap some of the moisture from your breath and humidify the air you inhale.
• Be Gentle: Avoid picking or aggressively rubbing your nose, as the tissues are more vulnerable.

Question  31. 

What is an altimeter? State its principle. How is its scale calibrated?

Ans:

What is an Altimeter?

An altimeter is a specialized instrument used to measure and display an object’s height above a fixed reference point, most commonly above mean sea level. It is a critical device in aviation, mountaineering, and skydiving, providing essential altitude information for navigation and safety.

The Principle of Operation

The fundamental principle behind the most common type of altimeter, the barometric altimeter, is the relationship between atmospheric pressure and altitude.

In simple terms: atmospheric pressure decreases predictably as you ascend into the atmosphere.

The altimeter is, at its core, a highly sensitive aneroid barometer. Instead of being calibrated to display units of pressure (like millibars or inches of Mercury), it is calibrated to display the corresponding altitude.

Here’s a breakdown of the principle:

1. The Core Component: Inside the instrument is a sealed, flexible metal capsule called an aneroid cell. This cell is evacuated of air.
2. Pressure Response: As the aircraft climbs and the outside atmospheric pressure drops, the aneroid cell expands. Conversely, as the aircraft descends into higher pressure, the cell contracts.
3. Mechanical Linkage: This tiny expansion and contraction is mechanically amplified through a series of levers and gears.
4. Display: This gearing ultimately moves the needles on the altimeter’s dial, indicating the calculated altitude.

The entire mechanism relies on the fact that the weight of the air column above the instrument lessens with height, and this change can be mechanically translated into a height reading.

How Its Scale is Calibrated

The scale of an altimeter is not calibrated with a simple, fixed formula because atmospheric pressure at sea level is not constant. It changes daily with weather systems (high and low pressure). Therefore, the calibration is a two-step process involving a reference setting that pilots must adjust.

The calibration is based on a standardized model of the atmosphere, known as the International Standard Atmosphere (ISA). The ISA assumes a specific sea-level pressure (1013.25 hPa or 29.92 inHg) and a standard rate at which temperature and pressure decrease with altitude.

The critical calibration is done through a knob on the altimeter’s face, which adjusts the reading by changing the reference pressure inside the instrument. This allows for two primary settings:

1. QNH Setting (Altitude Above Sea Level):
   • Principle: The pilot sets the local barometric pressure at sea level, which they obtain from an air traffic control tower or a weather station.
   • Calibration Effect: When the pilot dials in the QNH setting, the altimeter is mechanically recalibrated to read zero at ground level at that location. It then displays the aircraft’s height above mean sea level. This is used for local operations and when flying in the vicinity of an airport, ensuring all aircraft have a consistent altitude reference relative to the ground and obstacles.
2. Standard Pressure Setting (1013.25 hPa / 29.92 inHg – Flight Level):
   • Principle: For high-altitude flight where aircraft are separated from each other, a universal reference is needed to avoid conflicts caused by different local pressures.
   • Calibration Effect: When the pilot sets the standard pressure, the altimeter no longer displays true altitude above sea level. Instead, it displays a pressure altitude. All aircraft flying at high levels use this same setting. This ensures that even if their altimeters don’t show the exact height above the ground, they are all using the same reference point, maintaining safe vertical separation from each other. An altitude read under this setting is called a “Flight Level” (e.g., FL360 means 36,000 feet according to the standard pressure setting).

Question  32. 

1. What do the following indicate in a barometer regarding weather : gradual fall in the mercury level 

2. What do the following indicate in a barometer regarding weather : sudden fall in the mercury level 

3. What do the following indicate in a barometer regarding weather : Gradual rise in the mercury level?

Ans:

1. Gradual Fall in the Mercury Level

A slow, steady decline in the barometer’s mercury is a reliable signal of a shift in the weather pattern. Think of it as the atmosphere slowly losing its grip. This occurs when a large area of lower atmospheric pressure is approaching your location, gradually replacing the denser, high-pressure air. Such a change doesn’t typically bring immediate drama. Instead, it acts as a slow-burning fuse.

This gradual fall often foretells a sustained period of deteriorating conditions. You can expect the skies to become increasingly overcast, with winds picking up from a southeasterly direction. It is a strong indicator that a prolonged period of rain or general unsettled weather is on the horizon, likely arriving within a day or two. It’s the atmosphere’s way of giving a prolonged, gentle warning.

2. Sudden Fall in the Mercury Level

A rapid and sharp drop in the mercury level is one of the most critical and urgent signals a barometer can give. This isn’t a slow shift but a violent collapse in atmospheric pressure. It indicates that an intense low-pressure system, with a very steep pressure gradient, is barreling towards you.

This is a classic precursor to stormy and potentially violent weather. Such a reading demands immediate attention, as it signals the likely arrival of gale-force winds, heavy downpours, and thunderstorms. In extreme cases, especially in tropical regions, a sudden, deep plunge can be a warning sign for an approaching hurricane or cyclone. The weather can deteriorate with startling speed following such a reading.

3. Gradual Rise in the Mercury Level

A steady climb in the mercury column signifies that the weight of the atmosphere is increasing as a high-pressure system builds or moves over your area. High-pressure acts like an atmospheric “dome,” suppressing cloud formation and calming the winds.

Therefore, a gradual rise is a very positive omen for weather improvement. It indicates that any current poor weather—such as rain, clouds, or wind—will begin to clear. It promises a shift towards stable, calm, and clear conditions. You can anticipate sunnier skies, lighter winds, and generally pleasant, settled weather for the foreseeable future. It is the barometer’s way of signaling that fair weather is firmly establishing itself.

Exercise 4 (B)

Question 1. 

The unit torr is related to the barometric height as :

1.  1 torr = l cm of Hg 
2.  1 torr = 0.76 m of Hg
3. 1 torr = 1 mm of Hg
4. 1 torr = 1m of Hg

Question 2. 

The normal atmospheric pressure is : 

1. 76 m of Hg
2. 76 cm of Hg
3. 76 Pa
4. 76 N m-2

Question 3. 

The atmospheric pressure at earth’s surface is P1 and inside mine is P2. They are related as : 

1. P l =P2
2. P l > P2
3. P l <  P2
4. P2 = 0

Exercise 4 (B)

Question 1. 

Convert 1 mm of Hg into pascal. Take density of Hg = 13.6 x 103 kg m-3 and g = 9.8 m s-2 .

Ans:

We are tasked with finding the pressure in pascals that is equivalent to 1 millimeter of mercury (mmHg). The pressure exerted by a fluid column is given by the formula:

Pressure = Height of Column × Density of Fluid × Acceleration due to Gravity

In symbolic terms, this is:
P = hρg

Now, let’s use the provided values:

• Height, h = 1 mm = 1 × 10⁻³ m
• Density, ρ = 13.6 × 10³ kg/m³
• Gravity, g = 9.8 m/s²

Substituting these values into the formula:
P = (1 × 10⁻³ m) × (13.6 × 10³ kg/m³) × (9.8 m/s²)

Let’s perform the multiplication step-by-step.

First, multiply the numerical coefficients and the powers of ten:
1 × 13.6 × 9.8 = 133.28

Now, handle the powers of ten:
10⁻³ × 10³ = 10⁰ = 1

So, combining everything:
P = 133.28 kg/(m·s²)

The unit kg/(m·s²) is defined as a Pascal (Pa).

Therefore,
1 mm of Hg = 133.28 Pa

Question 2. 

At a given place, a mercury barometer records a pressure of 0.70 m of Hg. What would be the height of the water column if mercury in the barometer is replaced by water? Take the density of mercury to be  = 13.6 × 103 kg m-3.

Ans:

A barometer operates on a fundamental physical concept: the weight of a vertical column of liquid is supported by, and therefore equal to, the pressure exerted by the atmosphere. When the barometer is in a steady state, the atmospheric pressure pushing up on the liquid in the reservoir perfectly balances the downward pressure from the weight of the liquid column in the tube.

In this scenario, we are told that the atmospheric pressure corresponds to a mercury column height of 0.70 meters. The goal is to determine what height a column of water would reach under this identical atmospheric pressure.

The pressure generated by any fluid column is calculated using the formula:
Pressure = Fluid Density × Acceleration due to Gravity × Height of Column

Since the atmospheric pressure is the same in both cases, we can set the pressures equal to each other:

Density of Mercury × g × Height of Mercury = Density of Water × g × Height of Water

The acceleration due to gravity (g) is a common factor on both sides and can be cancelled out, simplifying our equation to:

Density of Mercury × Height of Mercury = Density of Water × Height of Water

This simplified equation directly relates the densities and heights, showing that for a given pressure, the height of the fluid column is inversely proportional to its density. A denser fluid like mercury will have a shorter column, while a less dense fluid like water will need a much taller column to exert the same pressure.

We can now solve for the unknown height of the water column:

Height of Water = (Density of Mercury × Height of Mercury) / Density of Water

Plugging in the provided values:

• Density of Mercury = 13,600 kg/m³
• Height of Mercury = 0.70 m
• Density of Water = 1,000 kg/m³

The calculation proceeds as follows:
Height of Water = (13,600 kg/m³ × 0.70 m) / 1,000 kg/m³
Height of Water = (9,520) / 1,000
Height of Water = 9.52 meters

Therefore, to measure the same atmospheric pressure, a water barometer would require a column approximately 9.52 meters tall. This significant difference highlights why mercury, being exceptionally dense, is a more practical liquid for constructing barometers of a manageable size.

Question 3. 

At sea level, the atmospheric pressure is 76 cm of Hg. If air pressure falls by 10 mm of Hg per 120m of ascent, what is the height of a hill where the barometer reads 70 cm Hg. State the assumption made by you.

Ans:

The height of the hill is 720 meters.

Assumption: The calculation assumes that the atmospheric pressure decreases uniformly with height, meaning the rate of pressure drop (10 mm of Hg per 120 meters) is constant. This implies that the temperature and air density are considered uniform throughout the atmosphere, which is not strictly true in reality as pressure decreases exponentially with height. However, for this problem, a linear decrease is assumed based on the given rate.

Question 4. 

At sea level, the atmospheric pressure is 1.04 x 105 Pa. Assuming g = 10 m s-2 and density of air to be uniform and equal to 1.3 kg m-3, find the height of the atmosphere.

Ans:

Question 5. 

Assuming the density of air to be 1.295 kg m-3, find the fall in barometric height in mm of Hg at a height of 107 m above the sea level. Take density of mercury = 13.6 × 103 kg m-3.

Ans:

The fall in barometric height is calculated using the formula derived from the pressure difference due to height change in a fluid. The pressure difference ΔP between sea level and a height h is given by ΔP = ρ_air g h, where ρ_air is the density of air. This pressure difference is equivalent to the pressure supported by a mercury column of height ΔH, so ΔP = ρ_Hg g ΔH. Equating these expressions and solving for ΔH gives:

ΔH = (ρ_air / ρ_Hg) h

To find ΔH in millimeters, convert h from meters to millimeters by multiplying by 1000:

ΔH (mm) = (ρ_air / ρ_Hg) h × 1000

Given:

• ρ_air = 1.295 kg/m³
• ρ_Hg = 13.6 × 10³ kg/m³ = 13600 kg/m³
• h = 107 m

Substitute the values:

ΔH = (1.295 / 13600) × 107 × 1000

First, calculate 1.295 / 13600 ≈ 0.000095220588

Then, 0.000095220588 × 107 ≈ 0.010188602

Finally, 0.010188602 × 1000 = 10.188602 mm

Considering significant figures, ρ_Hg has three significant figures (13.6), and h has three significant figures (107), so ΔH should be reported with three significant figures. Rounding 10.188602 mm to three significant figures gives 10.2 mm.

Thus, the fall in barometric height is 10.2 mm of Hg.