1. What is a Lens?
A lens is a transparent piece of glass with curved surfaces. The two main types are:
Convex Lens: Thick in the middle, thin at the edges. It converges (brings together) light rays.
Concave Lens: Thin in the middle, thick at the edges. It diverges (spreads out) light rays.
2. Key Terms
Optical Centre (O): The center point of the lens.
Principal Focus (F): The point where parallel rays meet (convex) or appear to come from (concave).
Focal Length (f): The distance between the optical centre (O) and the principal focus (F).
3. Image Formation
Convex Lens:
Object beyond 2F: Real, inverted, diminished.
Object between F and O: Virtual, erect, magnified (as in a magnifying glass).
Concave Lens: Always forms a virtual, erect, and diminished image.
4. Lens Formula & Power
Lens Formula: 1/f = 1/v – 1/u
(f = focal length, v = image distance, u = object distance)
Magnification (m): m = hᵢ/hₒ = v/u
Power (P): P = 1/f (with f in meters). Unit is Dioptre (D).
EXERCISE 5(A)
1.What is a lens?
Ans: A lens is a clear piece of glass or plastic shaped with a curved surface. It works by bending light rays as they pass through. This bending action lets a lens focus light to a single spot or spread it out wider. Because of this, lenses are essential parts of eyeglasses, cameras, microscopes, and telescopes.
2.Name the two kinds of lens. Draw diagrams to illustrate them.
Ans:
Two kinds of lenses are:
Convex Lens (Converging Lens)
Concave Lens (Diverging Lens)
Diagrams to Illustrate Them:
1. Convex Lens:
It is thicker at the centre and thinner at the edges.
It converges (brings together) light rays.
2. Concave Lens:
It is thinner at the centre and thicker at the edges.
It diverges (spreads out) light rays.
3.State difference between a convex and a concave lens in their (a) appearance, and (b) action on the incident light.
Ans:
(a) Appearance:
Convex Lens: Thicker at the centre and thinner at the edges.
Concave Lens: Thinner at the centre and thicker at the edges.
(b) Action on Incident Light:
Convex Lens: Converges (brings together) the incoming parallel rays of light to a single point called the focus.
Concave Lens: Diverges (spreads out) the incoming parallel rays of light so that they appear to be coming from a single point called the focus.
4.Which lens is converging: (i) an equiconcave lens or an equiconvex lens, (ii) a concavo-convex lens or a convexo-concave lens?
Ans: (i) Equiconvex lens vs. Equiconcave lens
An equiconvex lens is the converging lens. It is thicker at the center and causes parallel light rays to meet at a focus. An equiconcave lens is diverging, being thinner at the center and spreading parallel rays apart.
(ii) Concavo-convex lens vs. Convexo-concave lens
A concavo-convex lens is the converging lens. It has one concave and one convex surface, but the convex surface has a stronger curvature, making the center thicker. A convexo-concave lens is diverging because its concave surface has a stronger curvature, making the center thinner.
5.Out of the two lenses, one concave and the other convex, state which one will
show the divergent action on a light beam.
Ans: When a parallel beam of light passes through a concave lens, the rays are spread out (they diverge). This happens because a concave lens is thinner at the centre and thicker at the edges, causing the light rays to bend away from the principal axis.
In contrast, a convex lens, which is thicker in the middle, converges or focuses the light rays to a single point.
6.Show by a diagram the refraction of two light rays incident parallel to the principal axis on a convex lens by treating it as a combination of a glass slab and two triangular glass prisms.
Ans:
A convex lens can be thought of as a combination of a central glass slab and two triangular prisms placed base-to-base.
Diagram Description:
Central Part (Glass Slab):
Draw a rectangular block in the middle, representing the glass slab.
Two rays parallel to the principal axis pass through this slab.
According to the laws of refraction, these rays will suffer a lateral shift but emerge parallel to their original direction. The slab alone does not converge the light.
Upper and Lower Parts (Triangular Prisms):
Above and below the central slab, draw two triangular prisms with their bases towards the principal axis and apexes outwards.
When parallel rays enter these prisms, they bend towards the base of each prism upon refraction.
This causes the rays to converge towards the principal axis.
Resultant Effect:
The rays passing through the upper prism bend downwards, and the rays passing through the lower prism bend upwards. All the parallel rays converge to a single point on the principal axis, known as the principal focus (F). This demonstrates the converging action of a convex lens.
In short, the glass slab transmits light without changing its parallelism, while the prisms cause the convergence, together making the convex lens a converging device.
7.Show by a diagram, the refraction of two light rays incident parallel to the principal axis on a concave lens by treating it as a combination of a glass slab and two triangular glass prisms.
Ans:
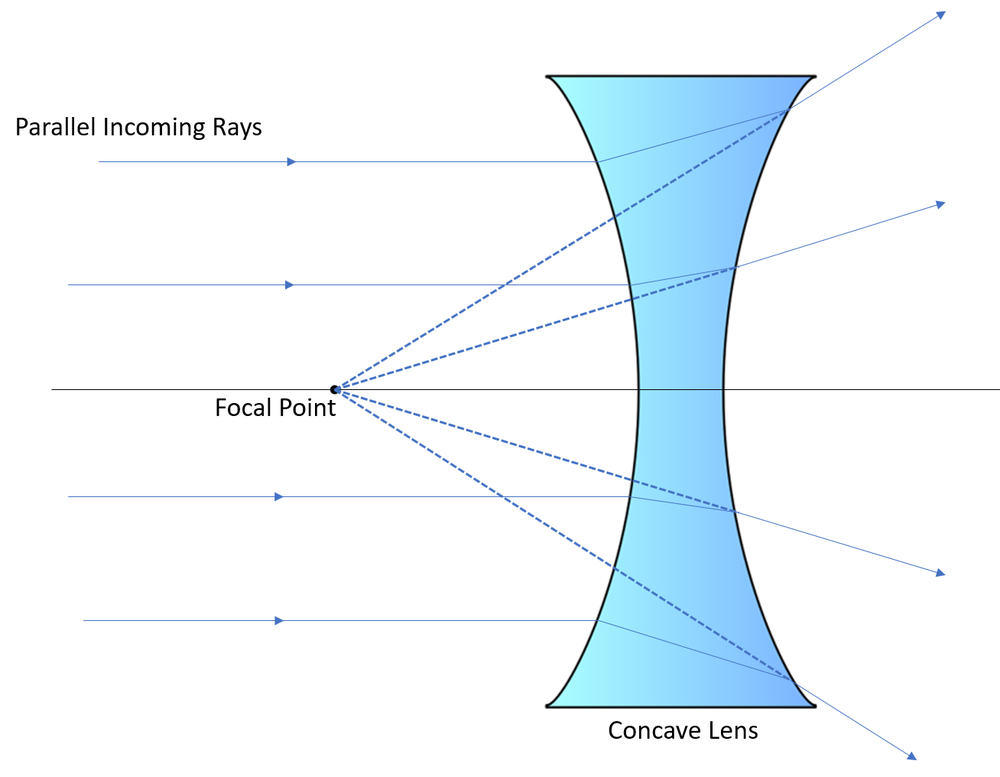
A concave (diverging) lens can be thought of as a central glass slab with two thin prisms placed base-outward at the edges.
Diagram Description:
Components shown:
A concave lens drawn with both surfaces curved inward.
It is represented as:
A rectangular glass slab in the middle (parallel-sided).
Two triangular prisms, one on each side of the slab, with their bases toward the edges and apexes toward the center.
Ray path:
Two rays parallel to the principal axis are shown incident on the lens:
One passes through the upper part (through the upper prism + slab).
One passes through the lower part (through the lower prism + slab).
In the glass slab (central part), the ray suffers a small lateral shift but emerges parallel to the incident direction.
In the prism sections, the ray is deviated away from the base of the prism (towards the thinner part) due to refraction.
Since the prism bases are at the edges of the lens, the deviation is away from the principal axis for both upper and lower rays.
Result:
The emergent rays diverge as if coming from a point on the principal axis — the virtual focus F of the concave lens.
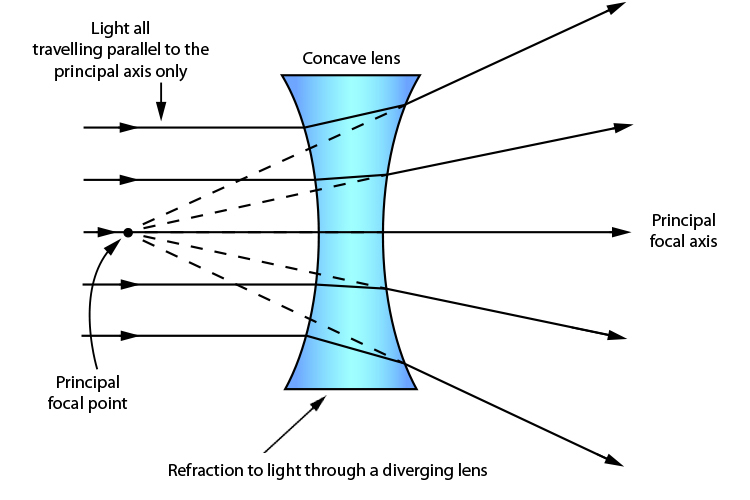
8.How does the action of a convex lens differ from that of a concave lens on a parallel beam of light incident on them? Draw diagrams to illustrate your answer.
Ans:
A convex lens (converging lens) causes a parallel beam of light to converge to a single point called the principal focus (F).
A concave lens (diverging lens) causes a parallel beam of light to diverge, such that the rays appear to be coming from a single point called the principal focus (F).
Diagram for a Convex Lens:
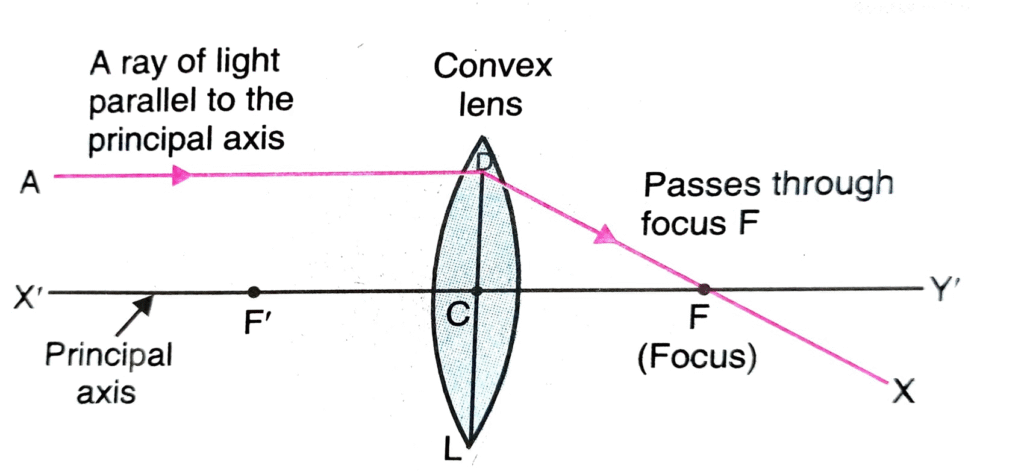
Diagram for a Concave Lens:
9.Define the term principal axis of a lens.
Ans:The principal axis is the main reference line for a lens. Think of it as the “centerline” that runs straight through the very middle of the lens.
Key Points:
It’s an imaginary line that passes through the lens’s optical center.
It acts as the primary guide in ray diagrams for predicting how light will behave.
Light rays traveling parallel to this central line are redirected through the focal point, which also lies on the axis.
10.Explain optical centre of a lens with the help of proper diagram(s).
Ans: Optical Centre of a Lens
The optical centre of a lens is a special point on the principal axis such that any ray of light passing through it does not suffer any deviation.
In simpler terms, a ray of light that is directed exactly towards the optical centre will pass straight through the lens in a straight line without bending.
Location: For a symmetric (like a double convex or double concave) lens with identical curved surfaces, the optical centre (O) lies exactly at the geometric centre of the lens.
Why does this happen?
The lens can be thought of as being made of two prisms placed base-to-base (for convex) or apex-to-apex (for concave). At the optical centre, the two surfaces of the lens are parallel to each other, like a glass slab. When light passes through a medium with parallel sides, the emergent ray is parallel to the incident ray but suffers a slight lateral shift. At the optical centre, this shift is negligible, resulting in the ray appearing to pass straight through without any deviation.
Diagram
The diagram below shows a ray of light passing undeviated through the optical centre (O) of a convex lens.
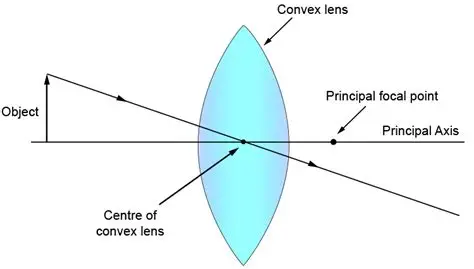
Explanation of the Diagram:
The vertical lines represent the boundaries of the convex lens.
Point O is the Optical Centre.
Ray A → O is the incident ray directed towards the optical centre.
Ray O → B is the emergent ray. It continues in the same straight line without any bending.
11.A ray of light incident at a point on the principal axis of a convex lens passes undeviated through the lens. (a) What special name is given to this point on the principal axis? (b) Draw a labelled diagram to support your answer in part
Ans:
(a) The special name given to this point on the principal axis is the Optical Centre of the lens.
(b) Labelled Diagram:
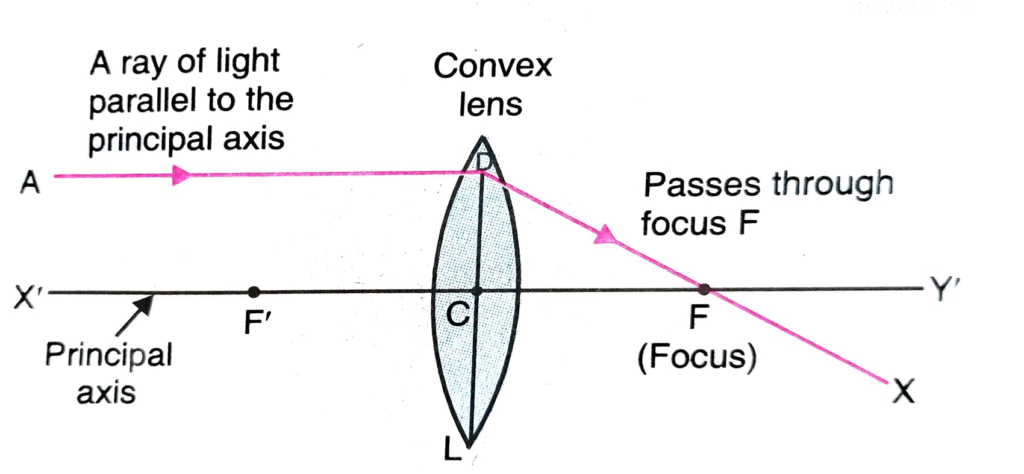
A labelled diagram supporting the answer is described below:
Draw a standard convex lens.
Mark its principal axis as a horizontal line passing through the lens.
Mark a point ‘O’ at the centre of the lens, where the principal axis intersects it. Label it as the “Optical Centre”.
Draw a ray of light travelling along a straight line that passes through point ‘O’. This ray should be drawn such that it is not parallel to the principal axis but still passes through ‘O’.
Show with arrows that the emergent ray on the other side of the lens is a straight continuation of the incident ray, indicating “No deviation”.
12.State the condition when a lens is called an equiconvex or equi-concave.
Ans: A lens is called equiconvex when both its surfaces are convex and have equal radii of curvature.
A lens is called equiconcave when both its surfaces are concave and have equal radii of curvature.
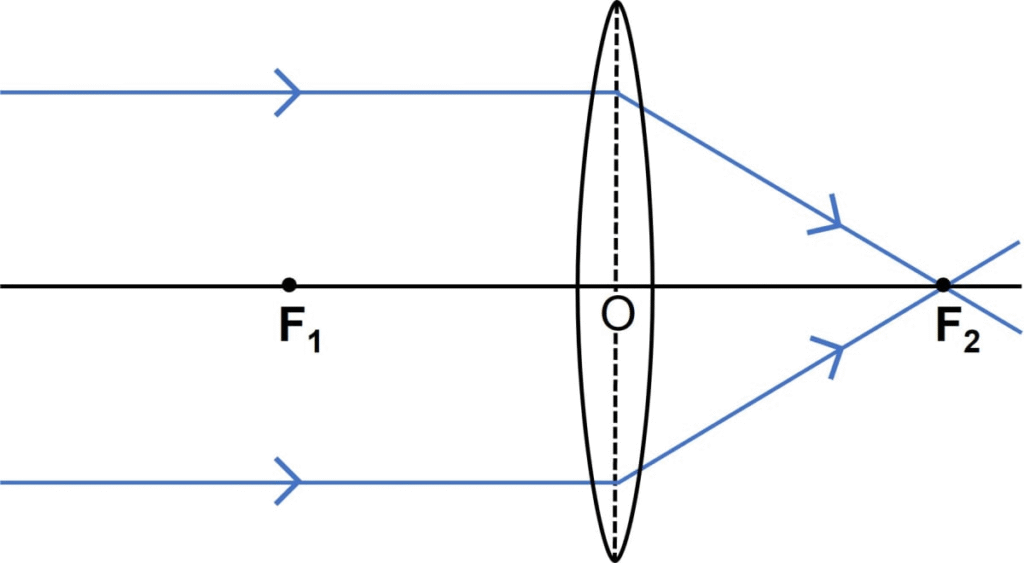
13.Define the term principal foci of a convex lens and illustrate your answer with the aid of proper diagrams.
Ans:
Principal Foci of a Convex Lens
The principal focus (or focal point) of a convex lens is a point on the principal axis where light rays parallel to the axis converge after passing through the lens.
A convex lens has two principal foci, one on each side, because light can approach from either direction.
Illustration with Diagram
Explanation of the Diagram:
The horizontal line is the Principal Axis.
The double-arrow O represents the Convex Lens.
The arrows —> and <— represent parallel rays of light traveling towards the lens.
The points marked F and F’ are the two Principal Foci.
All parallel rays converge at a focal point after refraction through the lens.
The distance between the center of the lens and either principal focus is the focal length.
14.Define the term principal foci of a concave lens and show them with the help of proper diagrams.
Ans:
Principal Foci of a Concave Lens
A concave lens is a diverging lens, thinner at the centre and thicker at the edges. It has two principal foci.
Definition: The principal focus (F) of a concave lens is the point on the principal axis from which incident parallel rays of light appear to diverge after passing through the lens.
Since light can come from either side, a concave lens has two principal foci, F₁ and F₂, located equidistant from the optical centre (O) on either side of the lens.
Ray Diagrams Showing the Principal Foci
Diagram 1: Focus for Light from the Left
A beam of light parallel to the principal axis is incident on the lens from the left.
After refraction through the concave lens, these rays diverge.When the refracted rays are extended backwards, they all appear to meet at a point (F₁) on the left side of the lens.This point F₁ is the principal focus.
Diagram 2: Focus for Light from the Right
Similarly, a beam of light parallel to the principal axis incident from the right side.
After refraction, the rays diverge and appear to come from a point (F₂) on the right side of the lens.This point F₂ is the second principal focus.
Key Point: For a concave lens, the principal focus is virtual because the light rays do not actually pass through it; it is the point from which they appear to diverge.
15.Draw a diagram to represent the second focus of a concave lens.
Ans: A concave lens has a virtual focus because the diverging rays do not actually meet. The second focus (F₂) is the point from which incident rays, parallel to the principal axis, appear to diverge after refraction.
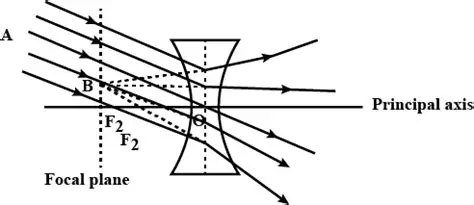
Diagram Description:
Draw a vertical line representing the concave lens.
Draw a horizontal principal axis through the center of the lens.
Mark a point F₂ (Second Focus) on the left side of the lens (for object space) on the principal axis.
Draw an arrow pointing towards the lens from the left, parallel to the principal axis.
At the lens, make this ray diverge. To show this, draw a dashed line backwards (to the left) from the lens, pointing directly towards F₂.
The diagram shows that the incident parallel ray, after refraction, appears to come from the virtual focus F₂.
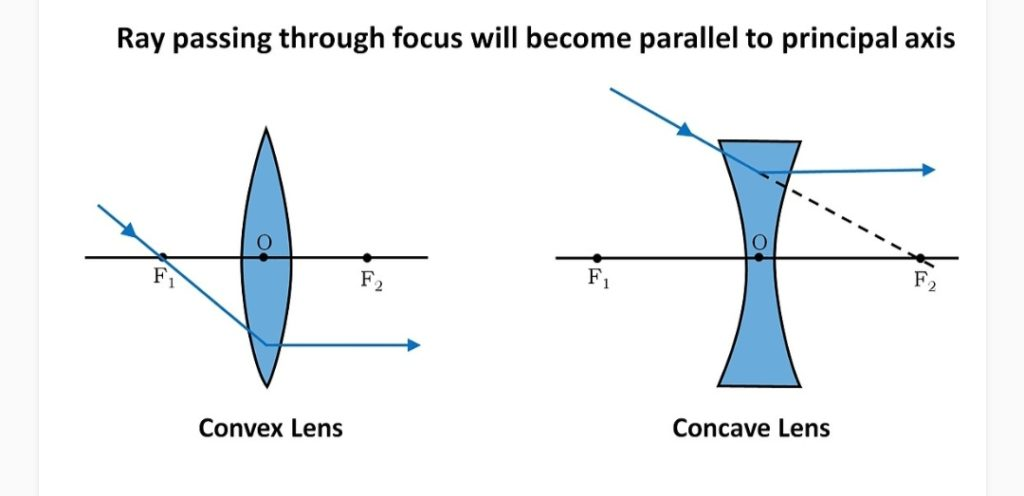
16.Draw a diagram to represent the second focus of a convex lens.
Ans: The second focus of a convex lens (F₂) is the point on the principal axis from which a beam of light, appearing to converge towards it, emerges parallel to the principal axis after refraction through the lens.
Diagram Description:
Draw a convex lens with its principal axis (a horizontal line through its center, O).
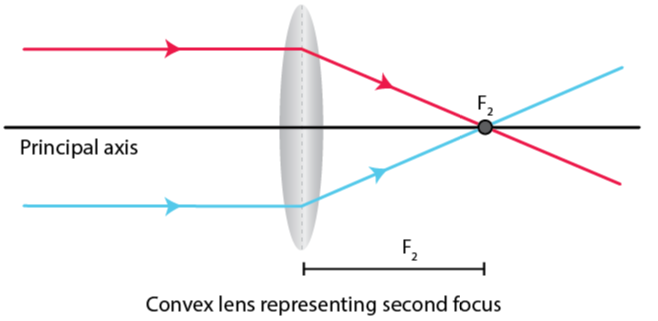
Mark the optical center (O) and the first focus (F₁) on the left side of the lens.
Mark the second focus (F₂) on the right side of the lens, at the same distance from O as F₁.
On the right side, draw an incident ray heading towards F₂ (a dotted line can be used to show its path beyond the lens if it didn’t refract).
At the lens, this ray refracts. Draw the emergent ray traveling parallel to the principal axis, moving to the left of the lens.
This diagram shows that F₂ is the virtual convergence point for the incident rays.
17.A ray of light, after refraction through a concave lens emerges parallel to the principal axis. (a) Draw a ray diagram to show the incident ray and its corresponding emergent ray. (b) The incident ray when produced meets the principal axis at a point F. Name the point F.
Ans:
(a) Ray Diagram Description
When an incident ray is directed towards the principal focus (F) located on the right side of a concave lens, the path of the ray after refraction is specific and predictable. As this incident ray travels towards F, it approaches the lens. Upon striking the concave lens and passing through it, the ray is refracted. Due to the diverging nature of the concave lens, the ray bends outward. The key observation is that after refraction, this particular ray emerges parallel to the principal axis. This behavior is a standard characteristic used in constructing ray diagrams for concave lenses.
(b) Definition of Point F
It is a specific point located on the same side of the lens as the incident light (the right side in this context) where light rays appearing to diverge from, or directed towards, seem to originate or aim after refraction. For a concave lens, this focus is virtual, meaning the refracted rays do not actually pass through point F, but their backward extensions do. This point is crucial for understanding the lens’s diverging effect.
18.A ray of light after refraction through a convex lens emerges parallel to the principal axis. (a) Draw a ray diagram to show it. (b) The incident ray passes through a point F on the principal axis. Name the point F.
Ans: (a) Ray Diagram
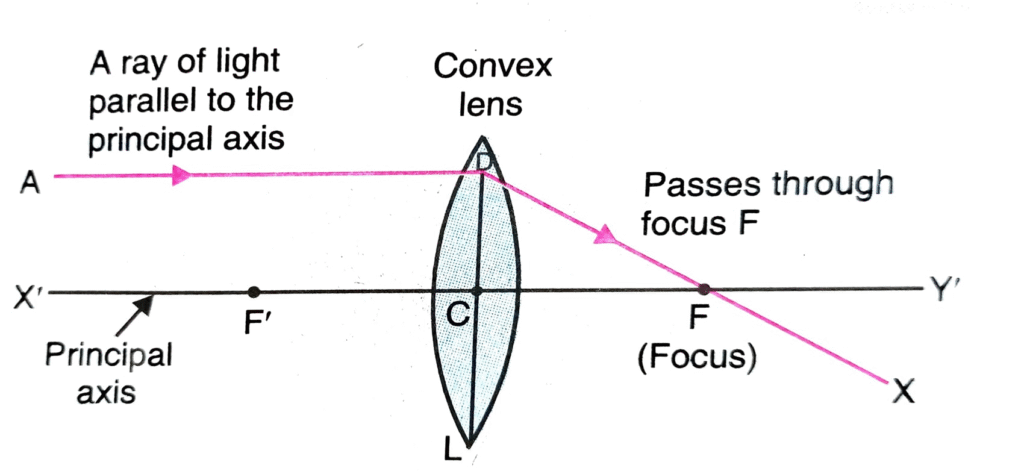
While I cannot draw a physical diagram here, I will describe it in detail so you can easily sketch it yourself.
Draw the Lens: First, draw a vertical double-headed arrow to represent a thin convex lens. Mark its optical centre as O.
Principal Axis: Draw a horizontal straight line passing through point O. This is the principal axis.
Locate Focal Point: Mark a point F on the left side of the lens, on the principal axis. The distance from O to F is the focal length.
Draw the Incident Ray: From point F, draw a ray going upwards and to the right, towards the lens. This is your incident ray.
Draw the Refracted Ray: When this incident ray reaches the lens, draw the refracted ray moving away from the lens in a direction perfectly parallel to the principal axis (to the right).
Your diagram will clearly show an incident ray diverging from point F, which, after passing through the convex lens, emerges as a ray parallel to the principal axis.
(b) Name the point F
The point F is called the First Principal Focus or simply the Focus of the convex lens.
19.A beam of light incident on a convex lens parallel to its principal axis converges at a point F on the principal axis. Name the point F. Draw a ray diagram to show it.
Ans: The point F is the principal focus of a convex lens.
Ray Diagram Description:
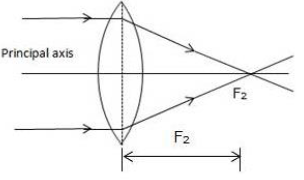
The diagram shows a convex lens with its principal axis, a horizontal line through its optical centre O.
Several light rays travel parallel to this axis from the left towards the lens. After passing through the lens, these rays bend inward and converge to meet at a single point F on the right side of the lens. This point, F, is clearly marked as the principal focus.
20.A beam of light incident on a thin concave lens parallel to its principal axis diverges and appears to come from a point F on the principal axis. Name the point F. Draw a ray diagram to show it.
Ans:
The point F is called the principal focus of the concave lens.
Ray Diagram Description:
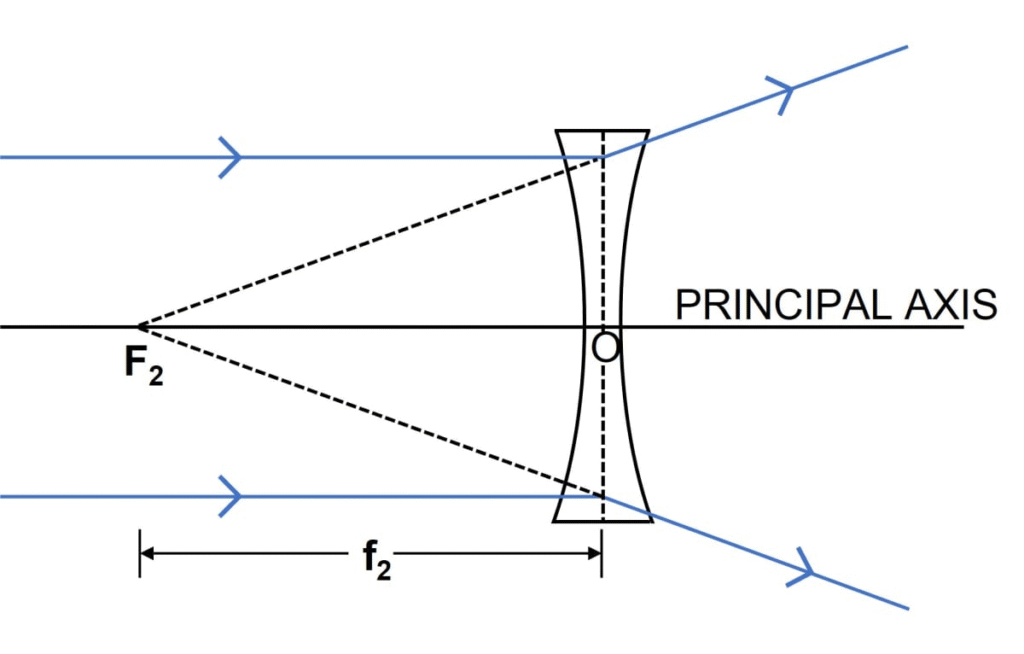
Draw a vertical line representing the concave lens. Mark its optical centre (O) on the principal axis.
Draw a horizontal line (principal axis) through O. Mark point F (principal focus) on the left side of the lens at an appropriate distance.
Draw a ray parallel to the principal axis incident on the lens. After refraction, this ray diverges away.
Extend the refracted ray backwards (using a dashed line). This extension passes through F on the same side of the lens as the incident ray.
To an observer on the right, the light appears to be coming from this point F.
21.Define the term focal length of a lens.
Ans: The focal length of a lens is a fundamental property that determines its optical power and field of view. It is defined as the distance between the optical centre of the lens and its principal focus (or focal point).To understand this better, consider a convex (converging) lens. When a beam of light rays parallel to the principal axis passes through this lens, the rays converge to meet at a single point on the other side. This point is the principal focus. The distance from the centre of the lens to this focal point is its focal length.In simpler terms, the focal length tells us how strongly a lens converges or diverges light.A short focal length means the lens bends the light rays very sharply, bringing them to a focus in a short distance. This indicates a stronger converging power and a wider field of view.A long focal length means the lens bends the light rays more gently, requiring a longer distance to focus them. This indicates a weaker converging power and a narrower, more magnified field of view.It is typically measured in millimetres (mm) and is a key factor in determining how a lens will form an image.
22.What do you mean by focal plane of a lens?
Ans: The focal plane is the flat surface where a lens brings parallel light rays to a sharp point. It is always located one focal length away from the lens. In a camera, the film or digital sensor is positioned precisely at this plane to capture a clear, in-focus image.
23.State the condition for each of the following:
(a) a lens has both its focal lengths equal.
(b) a ray passes undeviated through the lens.
Ans: (a) Condition for a lens to have both focal lengths equal:
The lens must have the same medium on both sides.
(b) Condition for a ray to pass undeviated through a lens:
The ray must pass through the optical centre of the lens.
24.A parallel oblique beam of light falls on a (i) convex lens, (ii) concave lens. Draw a diagram in each case to show the refraction of light through the lens.
Ans:
(i) Convex Lens
A parallel oblique beam of light is incident on the convex lens.
After refraction, the rays converge.
All rays meet at a single point on the focal plane (the plane perpendicular to the principal axis passing through the principal focus).
The image of the distant object (source of parallel rays) is formed at this point on the focal plane.
(ii) Concave Lens
A parallel oblique beam of light is incident on the concave lens.
After refraction, the rays diverge.
When these diverging rays are extended backwards, they appear to meet at a single point on the focal plane.
A virtual image of the distant object is formed at this point on the focal plane.
25.The diagram alongside shows a lens as a combination of a glass slab and two prisms.
(i) Name the lens formed by the combination.
(ii) What is the line XX’ called?
(iii) Complete the ray diagram and show the path of the incident ray AB after passing through the lens.
(iv) The final emergent ray will either meet XX’ at a point or appear to come from a point on XX’. Label the point as F. What is this point called?
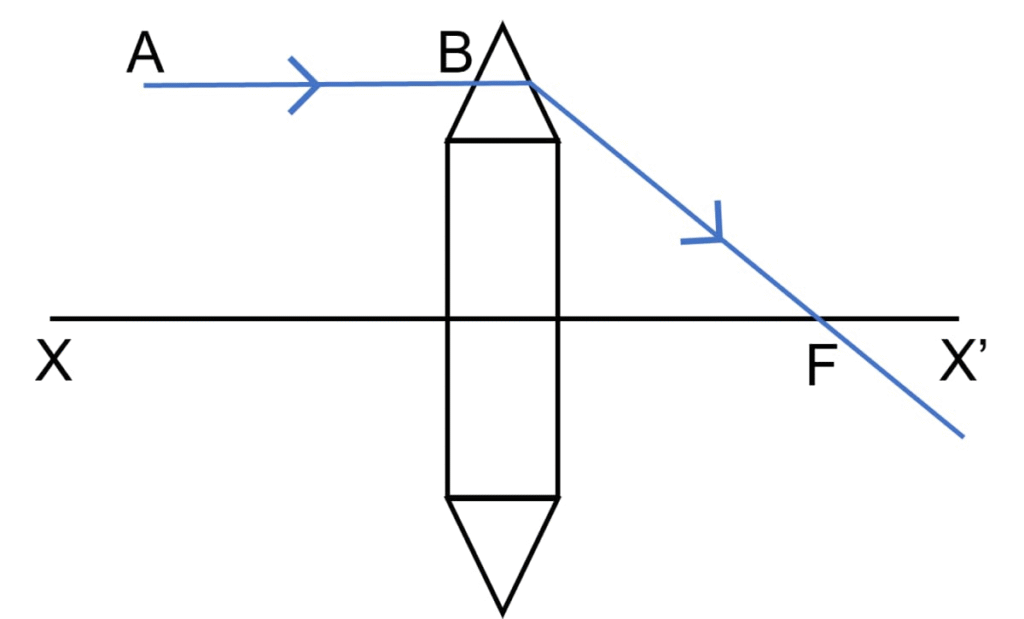
Ans: (i) Name the lens formed by the combination.
The combination of a glass slab and two prisms, as described, forms a Converging Lens (or a Convex Lens).
(ii) What is the line XX’ called?
The line XX’ is called the Principal Axis.
(iii) Complete the ray diagram and show the path of the incident ray AB after passing through the lens.
The completed path of the ray is as follows:
The incident ray AB, traveling parallel to the principal axis, enters the lens.
Upon entering the first prism, it refracts (bends) towards the base of the prism, which in this setup is towards the principal axis.
It then passes through the central glass slab, where it suffers a lateral shift but no net deviation.
As it exits through the second prism, it again refracts towards the base of this prism, which is also towards the principal axis.
The final emergent ray will pass through a specific point on the principal axis after exiting the lens.
(iv) The final emergent ray will either meet XX’ at a point or appear to come from a point on XX’. Label the point as F. What is this point called?
The point F where the emergent ray meets the principal axis is called the Principal Focus of the lens.
26.(i) Name the lens formed by the combination.
(ii) What is the line XX’ called?
(iii) Complete the path of the incident ray AB after passing through the lens.
(iv) The final emergent ray either meets XX’ at a point or appears to come from a point on XX’. Label it as F. What is this point called?
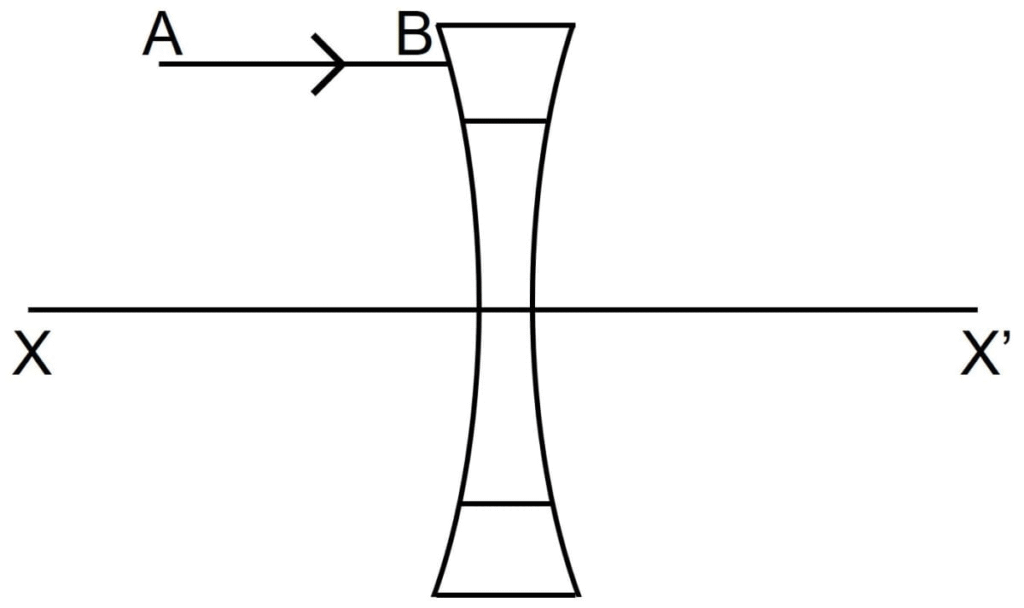
Ans:
(i) Name the lens formed by the combination.
The combination of a glass slab enclosed between two spherical bulging structures forms a Convex Lens. It is thicker at the centre and thinner at the edges, causing light rays to converge.
(ii) What is the line XX’ called?
The line XX’ is called the Principal Axis. It is the line that passes through the optical centre (O) of the lens and joins the centres of curvature of its two spherical surfaces.
(iii) Complete the path of the incident ray AB after passing through the lens.
The incident ray AB is parallel to the principal axis. When a ray parallel to the principal axis passes through a convex lens, it converges. Therefore, after passing through the lens, the ray will bend inward and cross the principal axis. The completed path would show the ray bending at the first surface (as it enters the glass), travelling through the glass slab, bending again at the second surface (as it exits into air), and finally converging to meet the principal axis at a specific point on the right side of the lens.
(iv) The final emergent ray either meets XX’ at a point or appears to come from a point on XX’. Label it as F. What is this point called?
This point F is called the Principal Focus of the lens. It is the point on the principal axis where all incident rays parallel to the axis converge after passing through the convex lens.
27.In Fig. 5.17, F1 and F2 are the positions of the two foci of the thin lenses shown in diagram (a) and (b). Draw the path taken by the light ray AB after it emerges from the lens in each diagram (a) and (b).
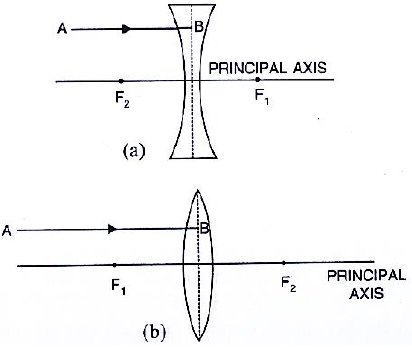
Ans: (a) Convex Lens (Converging):
Ray AB passes through focus F₁ before reaching the lens.
After refraction through the convex lens, it emerges parallel to the principal axis.
(b) Concave Lens (Diverging):
Ray AB is directed towards focus F₂ before reaching the lens.
After refraction through the concave lens, it emerges diverging away, appearing as if it came from the focus F₁ on the same side.
Path Summary:
(a) AB → Lens → Parallel to principal axis.
(b) AB → Lens → Diverges away from F₁.
28.In Fig. 5.18, F1 and F2a re the two foci of the thin lenses shown in diagram (a) and (b) and AB is the incident ray. Complete the diagram to show the path of the ray AB after refraction through the lens in each diagram (a) and (b).
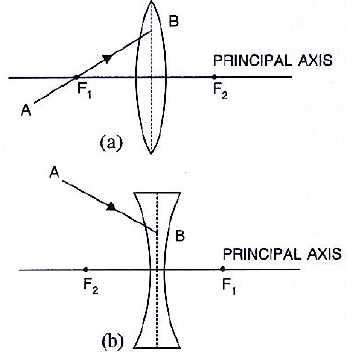
Ans: (a) Convex Lens:
Ray AB passes through optical center O without deviation.
After refraction, it passes through focus F₂ on the right side.
(b) Concave Lens:
Ray AB passes through optical center O without deviation.
After refraction, it appears to diverge from focus F₁ on the left side.
Completed Path:
In both diagrams, the ray AB goes straight through O.
In (a), it bends to pass through F₂.
In (b), it bends away as if coming from F₁.
29.Complete the following sentences :
(a) If half part of a convex lens is covered, the focal length …… change, but the intensity of image ……
(b) A convex lens is placed in water. Its focal length will ……
(c) The focal length of a thin convex lens is …… than that of a thick convex lens.
Ans:
(a) If half part of a convex lens is covered, the focal length does not change, but the intensity of image decreases.
(b) A convex lens is placed in water. Its focal length will increase.
(c) The focal length of a thin convex lens is more than that of a thick convex lens.
MULTIPLE CHOICE TYPE
1.A ray of light after refraction through a lens emerges parallel to the principal axis of the lens. The incident ray passes through :
(a) its optical centre
(b) its first focus
(c) its second focus
(d) the centre of curvature of the first surface.
Ans: (b) its first focus
2.A ray of light incident on a lens parallel to its principal axis, after refraction passes through or appears to come from :
(a) its first focus
(b) its optical centre
(c) its second focus
(d) the centre of curvature of its second surface.
Ans: (c) its second focus
EXERCISE 5(B)
1.What are the three principal rays that are drawn to construct the ray diagram for the image formed by a lens? Draw diagrams to support your answer.
Ans:
Principal Rays for Lens Ray Diagrams
Ray parallel to the principal axis:
After passing through the lens, this ray refracts and travels through the focal point on the other side (converging lens) or appears to come from the focal point on the same side (diverging lens).
Ray through the center of the lens:
This ray travels straight through the lens without any bending or deviation.
Ray through the focal point:
This ray travels towards the lens and, after refraction, emerges parallel to the principal axis (converging lens). For a diverging lens, a ray directed towards the focal point on the other side emerges parallel.
2.In the diagrams below, XX’ represents the principal axis, O the optical centre and F the focus of the lens. Complete the path of the rays A and B as they emerge out of the lens.
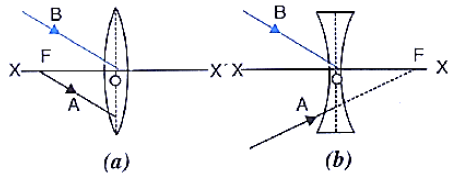
Ans: Ray A (parallel to principal axis):
After refraction through the convex lens, it bends inward and passes through the principal focus (F) on the opposite side.
Ray B (passing through optical centre):
It travels straight without any deviation, as rays through the optical centre of a thin lens do not bend.
3.Distinguish between a real and a virtual image.
Ans:
A real image is formed when light rays actually meet at a point after reflection or refraction. It can be projected onto a screen.
A virtual image is formed when light rays only appear to meet at a point when traced backward. It cannot be projected onto a screen.
4.Study the diagram (Fig. 5.48) given below.
(a) Name the lens LL’.
(b) What are the points O and O’ called?
(c) Complete the diagram to form the image of the object AB.
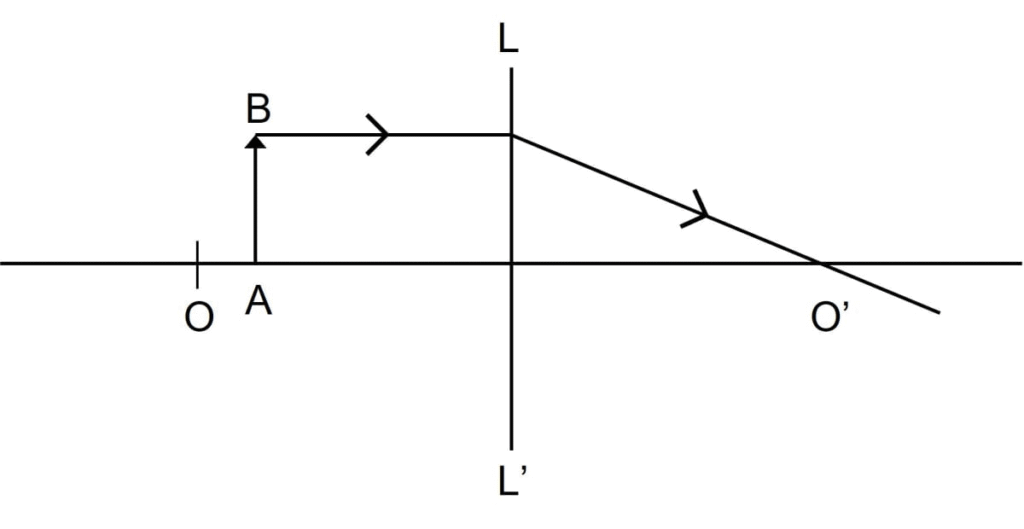
Ans: (a) The lens LL’ is a convex lens (or converging lens).
(b)
Point O is called the optical centre.
Point O’ is called the principal focus (or focal point).
(c) The completed ray diagram would show:
A ray from the top of the object (A), parallel to the principal axis, refracting through the lens and passing through the focal point (F/O’) on the other side.
A ray from the top of the object (A) passing straight through the optical centre (O) without bending.
The point where these two refracted rays meet locates the top of the real, inverted, and diminished image (A’B’), formed between F and 2F on the right side of the lens.
5. (a) Complete the diagram to show the formation of image A’B’ of the object of same size
(b) Name the lens LL’ and draw it outline
(c) What are the points O, O’ called?
(d) Where is the object Located ?.
(e) Where the image formed
(f) State two characteristics of the image.
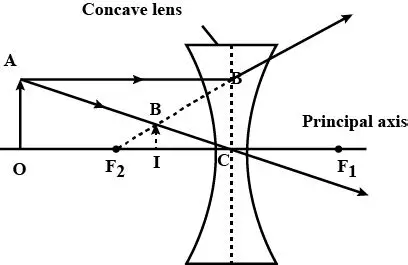
Ans: (a) Complete the diagram to show the formation of image A’B’ of the object of same size
To complete the diagram, draw the image A’B’ at the same distance on the opposite side of the lens, with the same size and orientation as the object AB. The image will be inverted.
(b) Name the lens LL’ and draw its outline
The lens LL’ is a convex lens. Its outline is bulging outwards in the middle on both sides.
(c) What are the points O, O’ called?
Point O is the Optical Centre of the lens. Points O and O’ likely represent the Foci or Focal Points of the lens.
(d) Where is the object located?
The object is located at a distance of twice the focal length (2F) from the lens.
(e) Where is the image formed?
The image is formed on the opposite side of the lens, also at a distance of twice the focal length (2F) from the optical centre.
(f) State two characteristics of the image.
The image is real.
6. (i) Name the lens LL’. (ii) What are the points O, O’ called? (iii) Complete the diagram to form the image of the object AB. (iv) State three characteristics of the image.
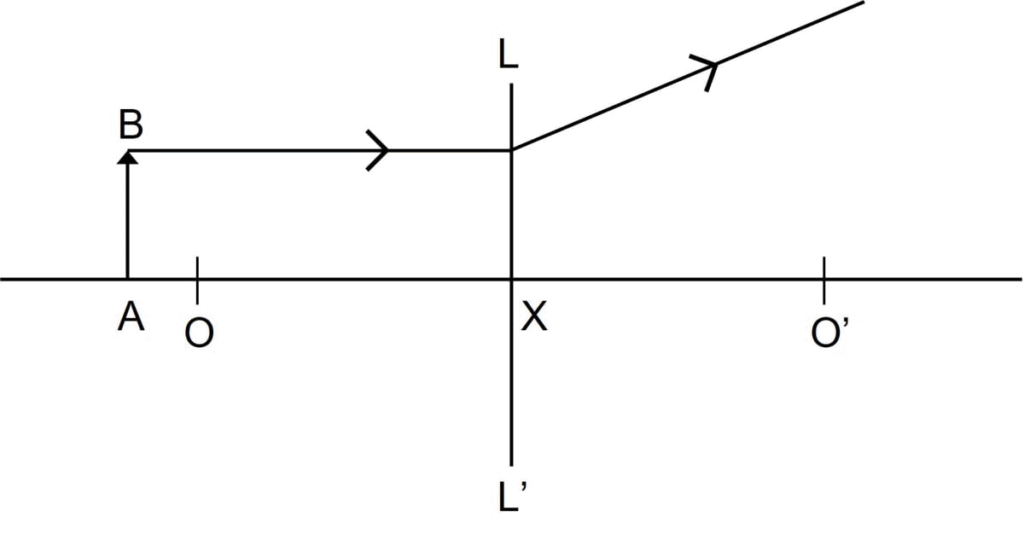
Ans: (i) The lens LL’ is a convex lens.
(ii) The points O and O’ are the principal foci (or focal points) of the lens.
(iii) The completed ray diagram is drawn below:
A ray from the top of the object (A), parallel to the principal axis, refracts through the lens and passes through the focal point (O’).
A ray from the top of the object (A), passing through the optical centre, goes straight without bending.
The two refracted rays converge at a point on the other side of the lens, forming the image A’B’ of the object AB.
(iv) Three characteristics of the image are:
Inverted
Magnified (or larger than the object)
7.(a) Draw two rays from the object AB and complete the diagram to locate the position of image CD. Also mark on the diagram the position of eye from where the image can be viewed.
(b) State three characteristics of the image in relation to the object.
Ans:(a) Diagram and Eye Position
A ray diagram should be drawn for a convex lens with the object (AB) placed between the focal point (F) and the optical centre of the lens.
Ray 1: After refraction through the lens, this ray will appear to diverge from the focal point (F) on the same side as the object.
Ray 2: Draw a second ray from the top of the object (A) passing straight through the optical centre of the lens without any deviation.
Image Formation: The two refracted rays will diverge on the same side as the object. To locate the image (CD), extend these diverging rays backwards using dotted lines. The point where these dotted lines meet is the position of the top of the virtual image (C). The image CD will be virtual, erect, and magnified.
Eye Position: The eye should be placed on the same side of the lens as the image (and the object), receiving the diverging rays of light.
(b) Three Characteristics of the Image
In relation to the object, the image formed is:
Virtual (cannot be projected on a screen).
Erect (upright, same orientation as the object).
Magnified (larger than the object).
8.(i) Draw two rays to locate the position of image.
(ii) State the position of image with reference to the lens.
(iii) Describe three characteristics of the image.
(iv) Describe how the distance of image from the lens and its size change as the object is moved towards F₁.
Ans:
(i) Draw two rays to locate the position of the image.
Ray 1: A ray parallel to the principal axis, which after refraction through the lens, passes through the principal focus (F₂) on the other side.
Ray 2: A ray passing through the optical centre (O) of the lens, which goes straight without any deviation.
The point where these two refracted rays intersect is the position of the top of the image.
(ii) State the position of image with reference to the lens.
The image is formed beyond 2F₂ (on the other side of the lens).
(iii) Describe three characteristics of the image.
Inverted (upside down)
Magnified (larger than the object)
(iv) Describe how the distance of image from the lens and its size change as the object is moved towards F₁.
As the object is moved from its initial position towards the focus F₁:
The distance of the image from the lens increases (it moves farther away from the lens).
The size of the image becomes larger (it keeps on magnifying).
9.A converging lens forms the image of an object placed in front of it beyond 2F2 of the lens.
(a) Where is the object placed?
(b) Draw a ray diagram to show the formation of image.
(c) Where is the image formed?
(d) State three characteristics of the image
Ans:(a) Where is the object placed?
The object is placed between F₁ and 2F₁ (or simply, between the focal point F and the centre of curvature 2F on the object side).
(b) Draw a ray diagram to show the formation of the image.
A simple ray diagram would show:
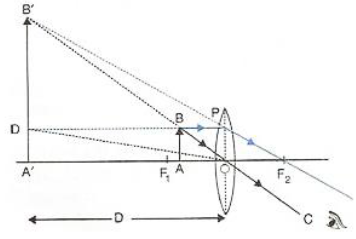
A Converging Lens with its principal axis, optical centre (O), and points F₁, 2F₁ (on the left) and F₂, 2F₂ (on the right) marked.
An object (an upright arrow labeled ‘AB’) placed between point 2F₁ and F₁ on the left side of the lens.
Two rays emanating from the top of the object (Point A):
Ray 1: A ray traveling parallel to the principal axis. After refraction, it passes through the focal point F₂ on the right.
Ray 2: A ray passing through the optical centre O that continues in a straight line without any deviation.
The two refracted rays converge at a point on the right side of the lens, beyond point 2F₂. This point is the top of the image (Point A’).
An inverted arrow labeled ‘A’B” is drawn from the principal axis to this point, representing the real and inverted image.
(c) Where is the image formed?
The image is formed beyond 2F₂ (i.e., beyond the centre of curvature on the opposite side of the lens).
(d) State three characteristics of the image.
The three main characteristics of the image are:
Real (because the light rays actually converge to form the image).
Inverted (upside down relative to the object).
Magnified (larger than the object).
10 . The following diagram in given below shows an object OA and its virtual image IB formed by a lens.

Ans: The object, labeled OA, is positioned between the optical centre and the focal point of a converging (convex) lens. Since the object resides within the lens’s focal length, the rays of light diverge after passing through the lens and do not meet on the opposite side. As a result, the image, labeled IB, is formed on the same side of the lens as the object itself.
The image IB possesses three key characteristics:
Virtual: The image is virtual because the light rays do not actually converge at the point where the image appears to be located. It cannot be projected onto a screen.
Erect: The image is oriented upright, in the same direction as the original object OA.
Magnified: The image is larger in size compared to the original object. This principle is the fundamental working mechanism of a simple magnifying glass.
11.The given below figure shows an object OA and its image IB formed by a lens.
(a) Name the lens and show it in the diagram.
(b) Draw suitable rays to locate the lens and its focus.
(c) State three characteristics of the image

Ans: (a) Name the lens and show it in the diagram.
The image formed is on the opposite side of the lens from the object and is inverted and real. It has been drawn in the diagram between the object (OA) and the image (IB).
(b) Draw suitable rays to locate the lens and its focus.
Two standard rays have been drawn:
A ray from the top of the object (A), parallel to the principal axis. After passing through the convex lens, this ray refracts and passes through the principal focus (F) on the other side.
A ray from the top of the object (A) that passes straight through the optical centre (O) of the lens without any deviation.
The point where these two refracted rays meet locates the top of the image (B). The lens is positioned at the optical centre (O), and the focal point (F) is located on the principal axis at the point where the initially parallel ray converges after refraction.
(c) State three characteristics of the image.
The three characteristics of the image (IB) are:
Real: The light rays actually converge at the point where the image is formed, meaning it can be projected onto a screen.
Inverted: The image is formed upside-down relative to the object.
Magnified: The size of the image is larger than the size of the object.
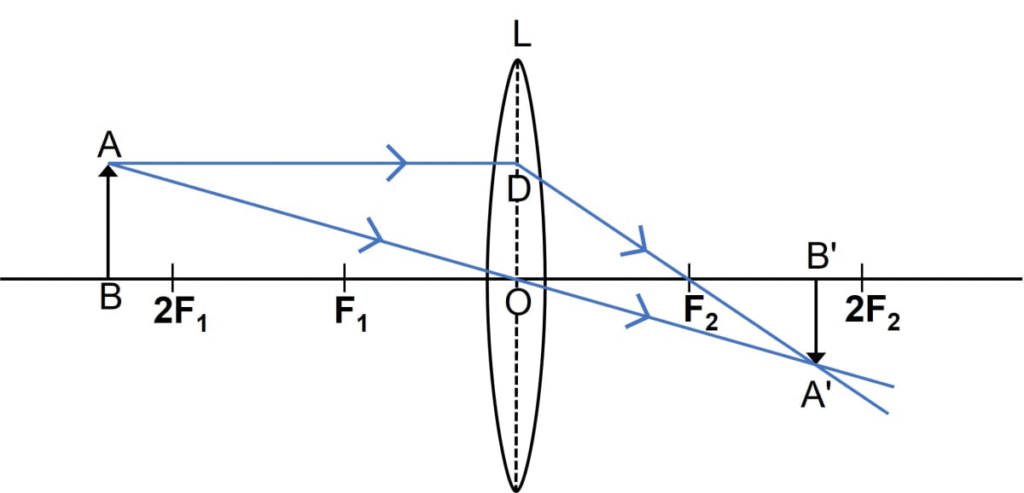
12. AConvex lens forms an image an object equal to size of object
(a) Where is the object placed in front of the lens?
(b) Draw a diagram to illustrate it.
(c) State two more characteristics of the image.
Ans: (a) Position of the Object
The object is placed at a distance equal to twice the focal length (2F) from the convex lens.
(b) Ray Diagram
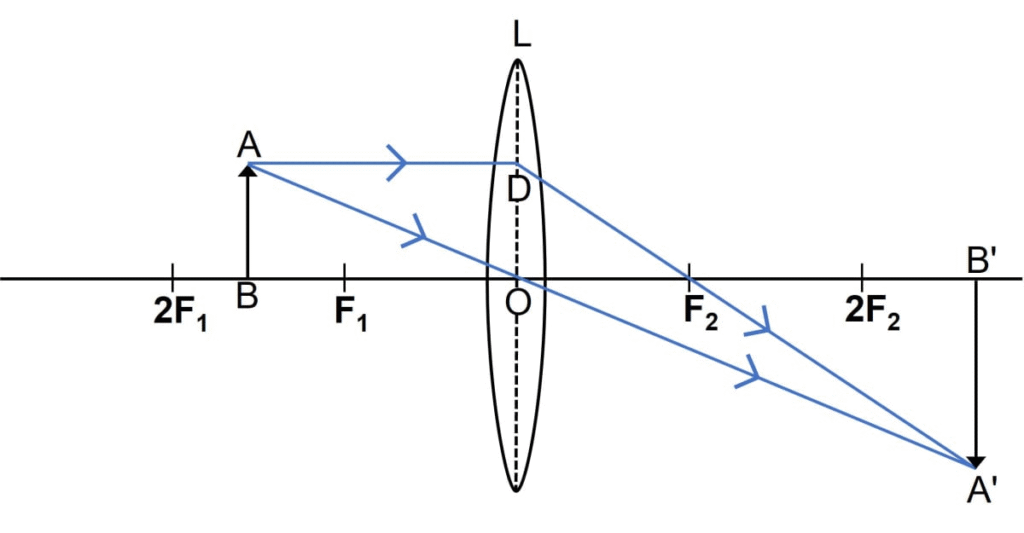
Description:
The object AB is placed at a distance of 2F from the optical centre O of the convex lens.
The image A’B’ is formed on the opposite side of the lens, also at a distance of 2F.
(c) Two More Characteristics of the Image
The image is real (can be obtained on a screen).
The image is inverted (upside down relative to the object).
13.A Lens forms an erect ,magnified and virtual image of an object
(a) Name the kind of lens.
(b) Where is the object placed in relation to the lens?
(c) Draw a ray diagram to show the formation of image.
(d) Name the device which uses this principle.
Ans:
(a) Kind of Lens
Convex lens
(b) Position of Object
Between the optical centre (C) and the principal focus (F₁) of the lens.
(c) Ray Diagram
A ray diagram would show:
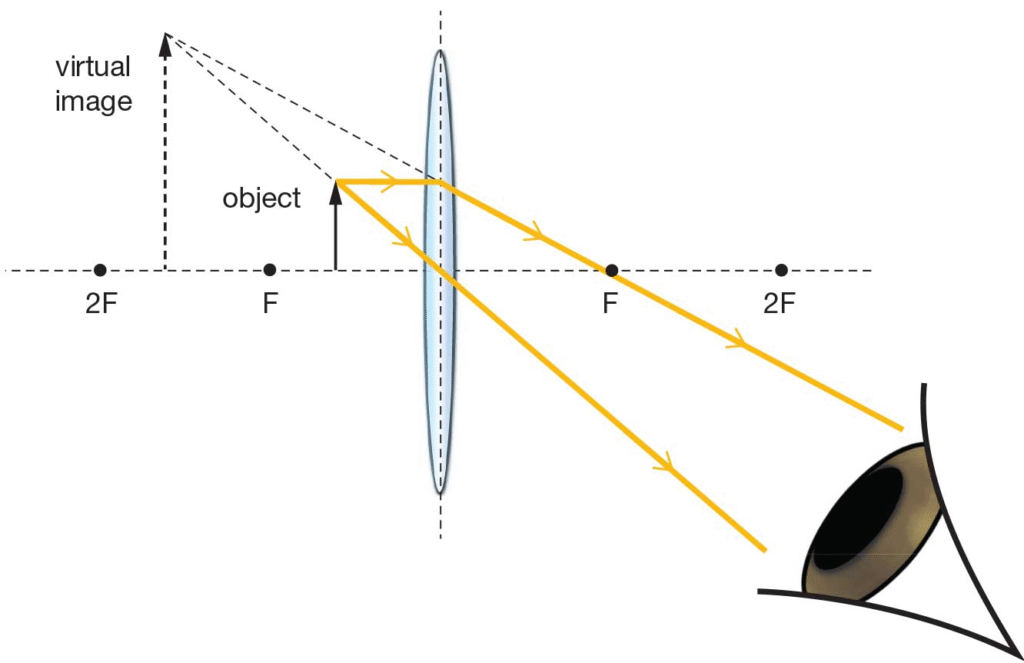
An object (an upright arrow) placed between the lens and its focus (F₁).
Two rays emerging from the top of the object:
One ray parallel to the principal axis, which refracts through the lens and passes through the focus (F₂) on the other side.
Another ray passing straight through the optical centre of the lens without deviation.
These two refracted rays appear to diverge on the same side of the lens as the object. Their backward extensions (shown as dotted lines) meet at a point to form the image.
The resulting image is virtual, erect, larger than the object (magnified), and located on the same side of the lens as the object.
(d) Device
A simple microscope or a magnifying glass uses this principle.
14.An object is placed on the axis of a lens. An image is formed by refraction in the lens. For all positions of the object on the axis of the lens, the positions of the image are always between the lens and the object.
(a) Name the lens.
(b) Draw a ray diagram to show it.
(c) State three characteristics of the image.
Ans: (a) The lens is a concave lens.
(b) Ray Diagram:

Explanation:
A ray (AB) parallel to the principal axis diverges after refraction, appearing to come from the focal point (F).
A ray (AC) directed towards the optical center passes straight without deviation.
The diverging rays appear to meet at a point when extended backwards, forming a virtual image between the lens and the object.
(c) Three characteristics of the image:
Virtual (cannot be projected on a screen)
Erect (upright, same orientation as the object)
Diminished (smaller than the object)
15. Classify as real or virtual, the image of a candle flame formed on a screen by a convex lens. Draw a ray diagram to illustrate how the image is formed.
Ans:
A real image is formed when light rays from an object actually meet after passing through a convex lens. This image can be projected onto a screen and is always inverted.
To form this image, place the candle beyond twice the focal length (2F) of the lens. Two key rays from the candle’s tip are drawn:
A ray parallel to the principal axis refracts through the focal point (F) on the opposite side.
A ray passing through the optical center continues straight without bending.
These refracted rays converge between F and 2F on the other side, forming a real, inverted, and diminished image on a screen placed at that location.
16. Show by a ray diagram that a diverging lens cannot form a real image of an object placed anywhere on its principal axis.
Ans:

When a diverging (concave) lens is used, the rays of light coming from an object always spread out after passing through the lens.
If the object is placed anywhere on the principal axis, the refracted rays diverge away from each other.
These rays never meet on the other side of the lens.
Since real image is formed where rays actually converge, a diverging lens cannot form a real image for any object position on the principal axis.
The ray diagram would show:
An object on the principal axis.
Rays from the object refracted by the lens such that they appear to come from a point on the same side as the object — forming a virtual, erect, and diminished image between the lens and the focus.
17. Draw a ray diagram to show how a converging lens can form a real and enlarged image of an object.
Ans:
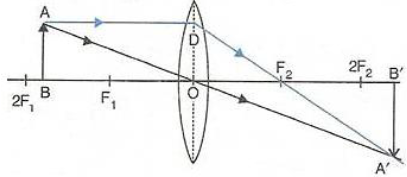
When an object (AB) is placed between the centre of curvature (C) and the principal focus (F) of a converging lens (convex lens), a real, inverted, and enlarged image (A’B’) is formed beyond C on the other side of the lens.
Ray Diagram Description:
A ray from the top of the object (A), parallel to the principal axis, passes through the principal focus (F) after refraction.
Another ray from point (A) passes through the optical centre (O) of the lens without any deviation.
These two refracted rays actually meet at point A’ on the other side of the lens.
Similarly, rays from point (B) meet at B’. Thus, A’B’ is the real, inverted, and enlarged image of the object AB.
18. Where will the image be formed if an object is kept in front of a concave lens at a distance equal to its focal length? Draw a ray diagram to illustrate your answer.
Ans: When an object is placed in front of a concave lens at a distance equal to its focal length, the image is formed between the optical centre and the focus on the same side as the object.
Characteristics of the Image:
Virtual
Erect
Diminished
Ray Diagram Description:

Draw a concave lens with its principal axis.
Mark the focus (F) on both sides of the lens.
Place the object at distance equal to focal length (at F) on the left side.
Draw a ray parallel to principal axis that appears to diverge from focus after refraction.
Draw a ray passing through optical centre that goes straight.
The diverging rays appear to meet between optical centre and F on the left side, forming a virtual, erect, and diminished image.
19. Draw a ray diagram to show how a converging lens is used as a magnifying glass to observe a small object. Mark on your diagram the foci of the lens and the position of the eye.
Ans: Ray Diagram Description:

Object Placement: The small object (AB) is placed between the optical centre (O) and the principal focus (F) of the converging lens (convex lens).
Ray Tracing:
A ray from the top of the object (A) is drawn parallel to the principal axis. After refraction through the lens, this ray passes through the principal focus (F) on the other side.
Another ray from point (A) is drawn passing straight through the optical centre (O) of the lens without any deviation.
Image Formation: The two refracted rays appear to diverge on the same side of the lens as the object. To locate the image, these rays are extended backwards as dotted lines.
Virtual Image: These dotted lines meet at point A’. This forms a virtual, erect, and magnified image (A’B’) on the same side as the object.
Marking the Diagram:
The two foci of the lens are marked as ‘F’ on both sides of the lens, at a distance equal to the focal length from the optical centre.
The eye is drawn on the same side as the image, receiving the diverging rays of light.
20. Draw a ray diagram to show how a converging lens can form an image of the sun. Hence give a reason for the term ‘burning glass’ for a converging lens used in this manner.
Ans:Ray Diagram Description:

A ray diagram is drawn showing a converging lens with the sun placed very far to the left. Two rays, drawn parallel to each other (representing rays from the distant sun), are incident on the lens. After refraction through the lens, these two rays converge and meet at a single point on the right side, known as the principal focus (F). The image of the sun is formed at this point.
Reason for the term ‘Burning Glass’:
A converging lens concentrates the intense light and heat energy from the sun onto a very small area at its focus. This concentrated energy produces a very high temperature at that point, which is sufficient to burn paper, char wood, or ignite flammable materials. It is this burning capability that gives a converging lens the name ‘burning glass’.
21. A lens forms an inverted image of an object.
(a) Name the kind of lens.
(b) State the nature of image whether real or virtual?
Ans: (a) Convex lens
(b) Real
Explanation: A convex lens produces an inverted image when the object is placed beyond its focal point. An inverted image formed by a lens is always real because the light rays physically meet at the image location.
22. A lens forms an upright and magnified image of an object.
(a) Name the lens.
(b) Draw a labelled ray diagram to show the image formation.
Ans:
(a) Name the lens.
The lens is a convex lens (converging lens).
(b) Labelled Ray Diagram
A simple labelled ray diagram would show:
Object: A vertical arrow (labeled “Object”) placed between the optical center (O) and the focal point (F) on the left side of the lens.
Lens: A convex lens (a line with outward-pointing arrows at the ends) at the center.
Focal Points: Points F and 2F marked on both sides of the lens.
Rays:
One ray from the top of the object, traveling parallel to the principal axis, which refracts through the lens and passes through the focal point (F) on the right side.
A second ray from the top of the object, passing straight through the optical center (O) without bending.
Image: The two refracted rays appear to diverge on the left side. Their backward extensions (shown as dotted lines) meet to form the image. This results in a vertical arrow (labeled “Image”) on the same side as the object. The image is virtual, erect, and magnified.
23. (a) Name the lens which always forms an erect and virtual image.
(b) State whether the image in part (a) is magnified or diminished.
Ans: (a) Name the lens which always forms an erect and virtual image.
Ans: The lens which always forms an erect and virtual image is a concave lens (also known as a diverging lens).
(b) State whether the image in part (a) is magnified or diminished.
Ans: The image formed by a concave lens is always diminished (smaller than the object), erect, and virtual, regardless of the position of the object.
24. An Lens forms an upright and diminished image of an object irrespective of an position .what kind of lens it is
Ans: The lens is a concave lens (also known as a diverging lens).
This is because a concave lens always produces an image that is:
Virtual (cannot be projected on a screen),
Upright (erect), and
Diminished (smaller than the object).
This characteristic holds true no matter where you place the object in front of the lens. A convex lens, on the other hand, can produce both inverted and upright images, and its images can be magnified or diminished depending on the object’s position. Since the problem specifies an upright and diminished image irrespective of the object’s position, it uniquely describes the behavior of a concave lens.
25. Give two characteristics of the image formed by a concave lens.
Ans:
The image is always virtual, meaning that the light rays do not actually meet but appear to diverge from a point. Therefore, this image cannot be obtained on a screen.
The image is always erect (upright) and diminished (smaller than the object), regardless of the object’s position.
26. Give two characteristics of the virtual image formed by a convex lens.
Ans: Two characteristics of the virtual image formed by a convex lens are:
It is erect (upright) and not inverted.
It is magnified (larger than the object).
27. In each of the following cases, where must an object be placed in front of a convex lens so that the image formed is
(a) at infinity,
(b) of same size as the object,
(c) inverted and enlarged,
(d) upright and enlarged?
Ans: (a) at infinity,
Answer: For the image to be formed at infinity, the object must be placed at the principal focus of the convex lens. In this position, the rays of light from the object become parallel after refraction through the lens.
(b) of same size as the object,
Answer: For the image to be of the same size as the object, the object must be placed at a distance equal to twice the focal length (i.e., at the center of curvature, 2F) of the convex lens. The image formed in this case will also be real, inverted, and located at 2F on the other side of the lens.
(c) inverted and enlarged,
Answer: To obtain an image that is inverted and enlarged, the object must be placed between the center of curvature (2F) and the principal focus (F) of the convex lens. The image will be formed beyond 2F on the opposite side and will be real and magnified.
(d) upright and enlarged?
Answer: To obtain an image that is upright and enlarged, the object must be placed between the principal focus (F) and the optical center of the convex lens. In this position, the image formed is virtual, erect, magnified, and located on the same side of the lens as the object. This is the principle used in a simple magnifying glass.
28. Complete the following table:
| Type of lens | Position of object | Nature of image | Size of image |
| Convex | Between optical centre and focus | Virtual and upright | Magnified |
| Convex | At focus | Real and inverted | Very much magnified |
| Concave | At infinity | Virtual and upright | Highly diminished |
| Concave | At any distance | Virtual and upright | diminished |
29. State the changes in the position, size and nature of the image when the object is brought from infinity up to the convex lens. Illustrate your answer by drawing the ray diagrams.
Ans: When an object is brought from infinity towards a convex lens, the position, size, and nature of the image change as follows:
(1) Object at Infinity:
Position: Image at focus (F′) on the other side.
Size: Highly diminished.
Nature: Real and inverted.
(2) Object beyond 2F:
Position: Image between F′ and 2F′.
Size: Diminished.
Nature: Real and inverted.
(3) Object at 2F:
Position: Image at 2F′.
Size: Same size as object.
Nature: Real and inverted.
(4) Object between F and 2F:
Position: Image beyond 2F′.
Size: Magnified.
Nature: Real and inverted.
(5) Object at F:
Position: Image at infinity.
Size: Highly magnified.
Nature: Real and inverted.
(6) Object between F and optical centre:
Position: Image on same side as object.
Size: Magnified.
Nature: Virtual and erect.
Ray Diagrams:
For each case, draw a convex lens with principal axis, mark F and 2F on both sides.
From object top, draw a ray parallel to principal axis, refracting through F′.
Another ray through optical centre going straight.
Where rays meet (or appear to meet) gives the image.
30. State the changes in the position, size and nature of the image when the object is brought from infinity up to the concave lens. Illustrate your answer by drawing the ray diagrams.
Ans: When an object is brought from infinity towards a concave lens, the changes in the image are as follows:
Position: The image always remains on the same side as the object, between the optical centre and the focus of the lens.
Size: The image is always smaller than the object (diminished). As the object comes closer, the image size increases slightly but remains smaller than the object.
Nature: The image is always virtual and erect.
Ray Diagram Illustration:
For an object at infinity, the image is at F₁ (focus), highly diminished, virtual, and erect.
As the object moves closer, the image moves slightly away from F₁ toward the lens but stays between F₁ and the optical centre.
When the object is very close to the lens, the image is also close to the lens but remains diminished, virtual, and erect.
These features can be shown in ray diagrams where rays diverge after refraction and appear to meet when extended back.
31. Complete the following sentences:
(a) An object is placed at a distance of more than 40 cm from a convex lens of focal length 20 cm. The image formed is real, inverted and……
(b) An object is placed at a distance 2f from a convex lens of focal length f. The size of the image formed is …… that of the object.
(c) An object is placed at a distance 5 cm from a convex lens of focal length 10 cm. The image formed is virtual, upright and ……
Ans:
(a) An object is placed at a distance of more than 40 cm from a convex lens of focal length 20 cm. The image formed is real, inverted and diminished
(b) An object is placed at a distance 2f from a convex lens of focal length f. The size of image formed is equal to that of the object.
(c) An object is placed at a distance 5 cm from a convex lens of focal length 10 cm. The image formed is virtual, upright and magnified
32. State whether the following statements are ‘true’ or ‘false’ by writing T/F against them.
(a) A convex lens has a divergent action and a concave lens has a convergent action.
(b) A concave lens, if kept at a proper distance from an object, can form its real image.
(c) A ray of light incident parallel to the principal axis of a lens, passes undeviated after refraction.
(d) A ray of light incident at the optical centre of lens, passes undeviated after refraction.
(e) A concave lens forms a magnified or diminished image depending on the distance of object from it.
Ans:
(a) False (F)
(b) False (F)
(c) False (F)
(d) True (T)
(e) False (F)
MULTIPLE CHOICE TYPE
1. For an object placed at a distance 20 cm in front of a convex lens, the image is at a distance 20 cm behind the lens. The focal length of convex lens is:
(a) 20 cm
(b) 10 cm
(c) 15 cm
(d) 40 cm
Ans: (b) 10 cm
2. For the object placed between the optical centre and focus of a convex lens, the image is:
(a) real and enlarged
(b) real and diminished
(c) virtual and enlarged
(d) virtual and diminished
Ans: (c) virtual and enlarged
3. A concave lens forms the image of an object which is:
(a) virtual, inverted, and diminished
(b) virtual, upright, and diminished
(c) virtual, inverted, and enlarged
(d) virtual, upright, and enlarged
Ans: (b) virtual, upright, and diminished
EXERCISE 5(C)
Question 1:
Define the term power of a lens. In what unit is it expressed?
Ans: Essentially, it tells us how strongly a lens can make light rays converge (come together) or diverge (spread apart). A lens with a high power will bend the light rays more sharply, bringing them to a focus over a shorter distance, while a lens with a low power will bend them more gently.
This power is quantified and expressed in a unit called the dioptre, which is represented by the symbol D. A simple way to understand this unit is that one dioptre is the power of a lens whose focal length is exactly one metre. So, if a lens has a power of +2 D, it is twice as strong as a lens of +1 D.
Question 2:
How is the power of a lens related to its focal length?
Ans: The power of a lens tells us how strongly it can bend or converge light rays. Think of it as a measure of the lens’s “strength.” This strength is directly linked to its focal length, which is the distance from the lens where it brings parallel light rays to a sharp focus.
The connection between them is beautifully simple and can be summed up in this way: Power is the reciprocal of the focal length. We write this relationship with the formula:
Power (P) = 1 / Focal Length (f)
However, there’s a crucial detail to remember for the units to work correctly. The focal length (f) in this formula must be measured in metres (m). The unit for power is the dioptre (D).
So, what does this mean in practice?
A lens with a short focal length is very “strong” or “powerful.” It can bend light rays sharply to bring them to a focus in a short distance. According to the formula, a small value for ‘f’ (in the denominator) results in a larger value for ‘P’. For example, a lens with a focal length of 0.25 metres has a power of 1 / 0.25 = 4 D.
A lens with a long focal length is “weaker.” It bends light rays more gently, requiring a greater distance to focus them. A large value for ‘f’ gives a smaller value for ‘P’. A lens with a focal length of 2 metres, for instance, has a power of 1 / 2 = 0.5 D.
Question 3:
How does the power of a lens change if its focal length is doubled?
Ans:
When the focal length of a lens is doubled, its power becomes halved.
This happens because the power of a lens (P) is inversely proportional to its focal length (f), as given by the formula:
P
=1f
Here, power is measured in dioptres (D) and focal length in metres.
For example:
If a lens has a focal length of 20 cm (0.2 m), its power is:
P=1/0.2=5D
If the focal length is doubled to 40 cm (0.4 m), the new power becomes:
P=1/0.4
=2.5D
So, doubling the focal length reduces the power to half of its original value
Question 4:
How is the sign (+ Or -) of power of a lens related to its divergent or convergent action?
Ans: The sign of a lens’s power indicates its action:
Positive (+) Power: This signifies a converging action. A convex lens has positive power as it bends light rays inward to meet at a focal point.
Negative (-) Power: This signifies a diverging action. A concave lens has negative power as it spreads light rays outward so they appear to come from a focal point.
.
Question 5:
The power of a lens is negative. State whether it is convex or concave?
Ans: If the power of a lens is negative, it is a concave lens.
This is because a concave lens is a diverging lens; it spreads out light rays that are passing through it. The negative sign of the power directly indicates this diverging action. In contrast, a convex lens, which converges light rays to a point, has a positive power.
Question 6:
What is magnifying glass? State its two uses.
Ans: A magnifying glass is a handy tool that acts like a simple microscope. At its heart is a convex lens, which is thicker in the middle than at the edges, and it’s specially designed with a short focal length. This lens is usually set in a frame, often with a handle to hold it comfortably over objects.
We use a magnifying glass primarily to make small things look bigger. Its two most common uses are:
Reading and Inspection: It’s perfect for making small text appear large and clear. People often use it to read fine print in books, on maps, or on medicine bottles. It’s also great for looking closely at details on stamps, coins, or fabrics, helping us see things that are normally too tiny for our eyes to focus on easily.
Precision Work: For people who work with very small components, a magnifying glass is essential. Watchmakers, for instance, rely on it to see the tiny gears and screws inside a watch. Similarly, jewellers use it to examine the details and settings in jewellery, and hobbyists building models or technicians working with electronics use it to handle and assemble small parts accurately.
Question 7:
Draw a neat labelled ray diagram to show the formation of image by a magnifying glass. State three characteristics of the image.
Ans: Object Position: The object (AB) is placed between the principal focus (F) and the optical centre of the convex lens.
Ray Diagram Description:

A ray from the object, drawn parallel to the principal axis, refracts through the lens and passes through the principal focus (F) on the other side.
A second ray from the object is drawn straight through the optical centre of the lens without any deviation.
These two refracted rays diverge after passing through the lens. To find the image, these rays are extended backwards (as dotted lines). The point where these backward extensions meet locates the virtual image (A’B’).
Three Characteristics of the Image:
Virtual
Erect
Magnified
Question 8:
Where is the object placed in reference to the principal focus of a magnifying glass, so as to see its enlarged image? Where is the image obtained?
Ans: To see an enlarged image using a magnifying glass, you need to place the object you’re looking at between the lens and its principal focus. Essentially, the object should be closer to the lens than its focal point.
When you position it this way, the image you see isn’t projected on a screen behind the lens. Instead, the enlarged image appears on the same side of the lens as the object. This image is not real; it’s virtual, which is why it looks larger and right-side up to your eye.
Question 9:
Define magnifying power of a simple microscope. How can it be increased?
Ans:
The magnifying power of a simple microscope is defined as the ratio of the angle subtended by the image at the eye to the angle subtended by the object when placed at the least distance of distinct vision (25 cm).
It can be increased by using a convex lens of shorter focal length.
Question 10:
Describe in brief how would you determine the approximate focal length of a convex lens.
Ans:
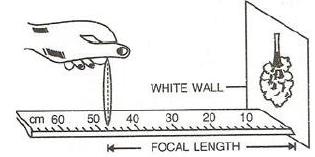
To determine the approximate focal length of a convex lens:
Setup: Hold the lens vertically using a stand, facing a distant object like a tree or building. Place a white screen (e.g., a paper) on the other side of the lens.
Adjust: Move the lens towards or away from the screen until a sharp, inverted image of the distant object is formed on the screen.
Measure: The distance between the centre of the lens and the screen at this point gives the approximate focal length of the convex lens.
This method works because for a distant object, the image forms at the focus of the lens.
Question 11:
The diagram in Fig. 5.68 shows the experimental set up for the determination of focal length of a lens using a plane mirror.
(i) draw two rays from the point O of the object to show the formation of image I at O itself.
(ii) What is the size of the image I?
(iii) State two more characteristics of the image I.
(iv) Name the distance of the objects O from the optical centre of the lens.
(v) To what point will the rays return if the mirror is moved away from the lens by a distance equal to the focal length of the lens?

Ans: (i) Ray Diagram: Two rays from O:
A ray parallel to the principal axis refracts through the lens and passes through focus F.
A ray through the optical centre C goes undeviated.
After reflecting from the mirror, both rays meet back at O, forming image I on the object itself.
(ii) Image Size: The image I is the same size as the object O.
(iii) Image Characteristics:
The image is real.
The image is inverted.
(iv) Object Distance: The object O is located at a distance from the optical centre equal to the focal length of the lens.
(v) Effect of Moving Mirror: If the mirror is moved away from the lens by a distance equal to the focal length, the rays from the lens become parallel. After reflection, these parallel rays converge at the focus F of the lens.
Question 12:
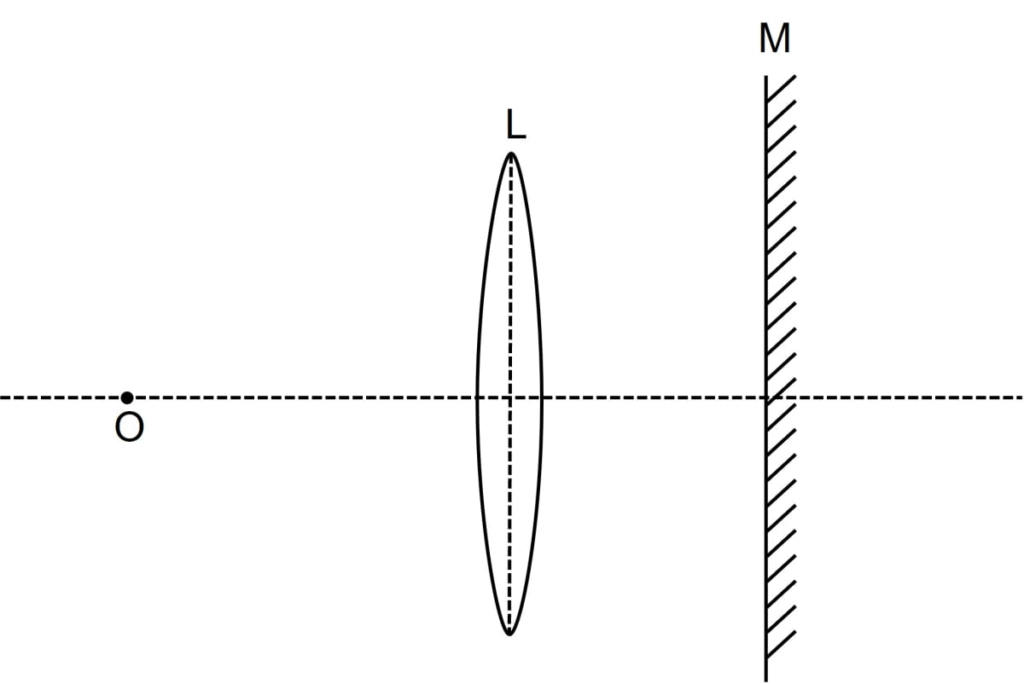
Describe how you would determine the focal length of a converging lens, using a plane mirror and one pin. Draw a ray diagram to illustrate your answer.
Ans: To find the focal length of a converging lens using a plane mirror and a pin:
Setup: Place the convex lens (L) on a horizontal plane mirror (MM). Now, arrange a pin (P) on a stand, positioning its tip vertically above the optical centre (O) of the lens.
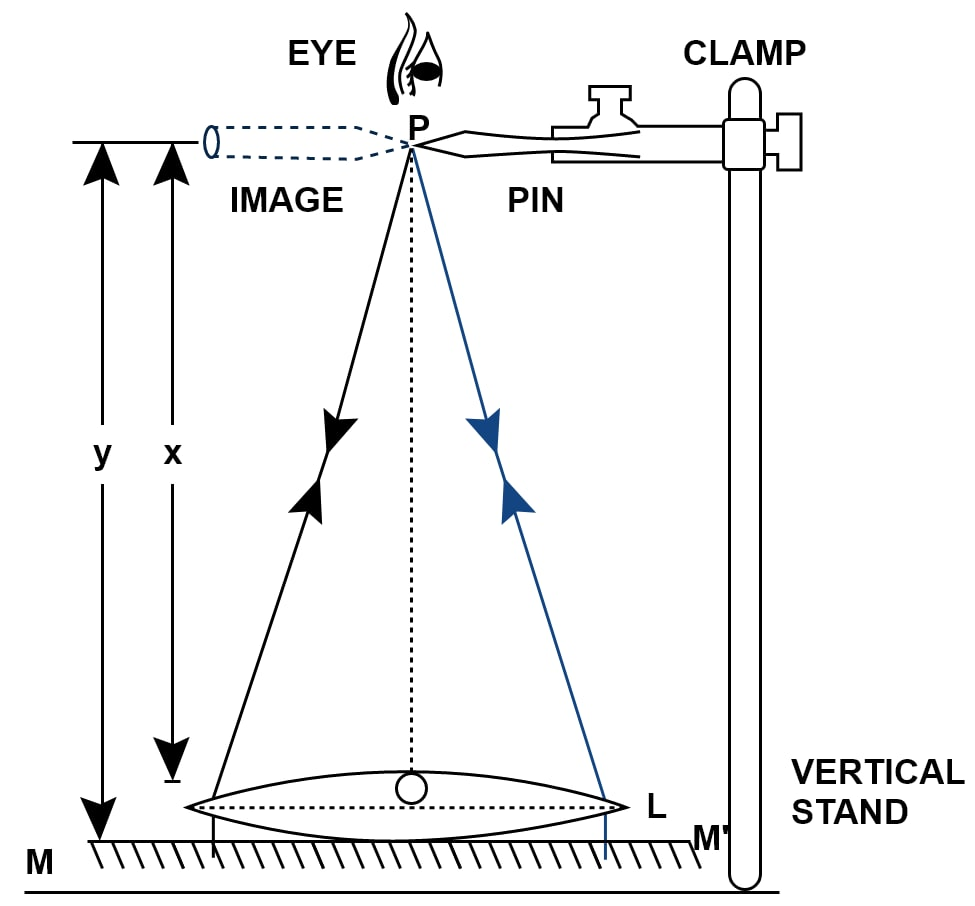
Adjustment: Move the pin up or down along the stand. From the top, look down through the lens at the pin’s image. Adjust the height until you see a clear, sharp image of the pin that does not move sideways relative to the pin itself when you move your head. This happens when the pin is at the lens’s focus, as the rays falling normally on the mirror retrace their path.
Measurement: In this position, the pin is exactly at the focal point. Measure the distance from the tip of the pin to the lens (or the mirror) using a metre scale. This distance is equal to the focal length (f) of the converging lens.
Ray Diagram:
[Draw a diagram showing:]
A convex lens (L) resting on a horizontal line representing a plane mirror (MM).
A pin (P) positioned vertically above the lens’s optical centre.
Two rays originating from the tip of the pin, parallel to the principal axis, going down towards the lens.
After refraction, these rays pass through the focal point (F) on the other side and hit the mirror.
The rays are reflected back by the mirror along the same path, finally meeting at the tip of the pin to form a sharp image. This shows the object (pin) is at the focus.
Question 13:
State two applications each of a convex lens and a concave lens.
Ans: Applications of a Convex Lens
A convex lens, which is thicker in the middle, bends light rays inward to meet at a focal point. This converging property makes it useful in many everyday tools.
As a Magnifying Glass: This is one of the most common uses. When you hold a convex lens close to a small object like text or an insect, it produces a larger, upright virtual image, making details easier to see. Jewelers, watchmakers, and hobbyists frequently use them for this precise reason.
In Cameras: Inside a camera, a convex lens focuses incoming light from a scene onto the camera’s film or digital sensor. By adjusting the lens’s position, it creates a sharp, real, and inverted image of the subject, which is then captured to create a photograph.
Applications of a Concave Lens
A concave lens, thinner in the middle, spreads out light rays as if they are coming from a focal point. This diverging property is harnessed in several important applications.
Correcting Nearsightedness (Myopia): People who are nearsighted have difficulty seeing distant objects clearly because the eye focuses images in front of the retina. Spectacles with concave lenses are used to correct this. The lenses diverge the light rays slightly before they enter the eye, which helps shift the focus point backward onto the retina, resulting in clearer distance vision.
In Door Peepholes: If you look through a peephole in a door, you can see a wide view of the outside area. This is possible because these viewers often contain a concave lens. The lens gives a wide-angle, reduced image of the hallway or porch, allowing you to identify a visitor without opening the door.
Question 14:
How will you differentiate between a convex and a concave lens by looking at (i) a distant object, (ii) a printed page?
Ans: (i) By looking at a distant object through the lens:
Hold the lens at arm’s length and look at a distant object, like a tree or a building, through it.
If you see an inverted (upside-down) image of the object, the lens is a convex lens. This happens because a convex lens converges light rays to form a real, inverted image of distant objects.
If you see an erect (upright) image of the object, the lens is a concave lens. A concave lens always diverges light rays, resulting in a virtual and erect image.
(ii) By looking at a printed page through the lens:
Place the lens close on top of a printed page and look through it.
If the letters appear larger and magnified than they actually are, the lens is a convex lens. A convex lens acts as a simple magnifying glass when the object is placed within its focal length.
If the letters appear smaller and diminished, the lens is a concave lens. A concave lens always reduces the apparent size of the object.
MULTIPLE CHOICE TYPE:
Question 1:
On reducing the focal length of a lens, its power:
(a) decreases
(b) increases
(c) does not change
(d) first increases then decreases
Ans: (b) increases
Question 2:
A magnifying glass forms:
(a) a real and diminished image
(b) a real and magnified image
(c) a virtual and magnified image
(d) a virtual and diminished image
Ans: (c) a virtual and magnified image
NUMERICALS:
Question 1:
The power of a lens is + 2.0 D. Find its focal length and state the kind of the lens.
Ans:The power of the lens is given as
P=+2.0D.
We know the relationship between power and focal length is:
P
=1/f
where f is the focal length in metres.
Substituting the given value:
+2.0= f/1
Solving for
f=1/2.0 =0.5m
Converting metres to centimetres:
f=0.5×100=50cm
A positive power indicates that the lens is a convex lens.
Final Answer:
The focal length is 50 cm, and the lens is a convex lens.
Question 2:
Express the power (with sign) of a concave lens of focal length 20 cm.
Ans: Step 1: Understanding the Problem
We are given a concave lens with a focal length of 20 cm. We need to calculate its power and include the correct sign.
Step 2: Recall the Formula for Power
P=1/f
where f is the focal length in meters.
Step 3: Convert Focal Length to Meters
Given focal length
f=20cm.
Since
1m=100cm,
f=20/100
=0.2m
Step 4: Calculate the Power
Substitute
f=0.2m into the formula:
P=10.2 =5D
Step 5: Apply the Correct Sign
A concave lens is a diverging lens, and its power is always negative.
Therefore,
P=−5D
Final Answer: −5 D


