Upthrust in Fluids, Archimedes’ Principle and Floatation

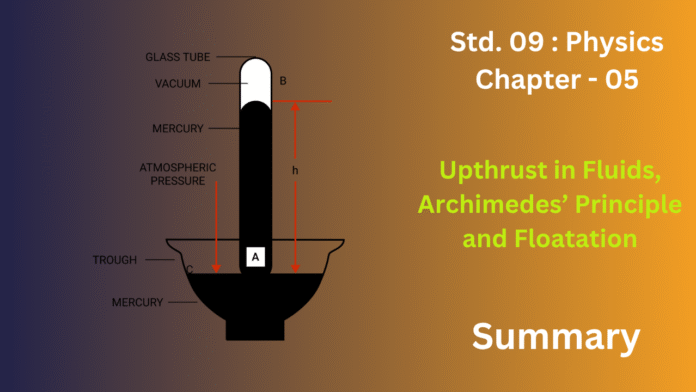
When an object is immersed in a fluid, which can be a liquid or a gas, it experiences an upward force that seems to push against its weight. This upward force is known as upthrust or buoyant force. It occurs because the pressure exerted by a fluid increases with depth. The pressure on the lower surface of the submerged object is greater than the pressure on its upper surface, resulting in a net upward force. The magnitude of this upthrust depends on two key factors: the density of the fluid itself and the volume of the fluid that the object displaces. Essentially, denser fluids and objects with a larger submerged volume will experience a stronger buoyant force.

This fundamental observation is perfectly captured by Archimedes’ Principle. It states that when a body is fully or partially immersed in a fluid, it experiences an upthrust equal to the weight of the fluid it has displaced. This means if you could collect the fluid that spills over when an object is submerged, the weight of that fluid would be exactly equal to the buoyant force pushing up on the object. This principle provides the scientific basis for why objects sink or float. Whether an object floats, sinks, or remains suspended is determined by the balance between its own weight and the upthrust acting upon it. An object will float if the upthrust (equal to the weight of displaced fluid) is greater than or equal to the object’s own weight. For a floating body, the weight of the entire object is equal to the weight of the fluid displaced by its submerged portion.

The principle of floatation has profound practical applications. It explains how massive steel ships, which are much denser than water, can float. This is achieved by shaping the ship into a hollow form, which increases its volume and displaces a very large amount of water. The weight of this displaced water equals the total weight of the ship and its cargo, allowing it to float. Similarly, submarines control their buoyancy by adjusting the amount of water in their ballast tanks, allowing them to dive or surface. Hot air balloons rise in the air because the hot air inside is less dense than the surrounding cooler air, making the balloon’s weight less than the upthrust from the displaced cooler air.

Exercise 5 (A)

Question 1. 

What do you understand by the term upthrust of a fluid? Describe an experiment to show its existence. 

Ans:

Understanding Upthrust

In simple terms, upthrust (also known as the buoyant force) is an upward force exerted by a fluid that opposes the weight of an object immersed in it. A fluid can be either a liquid or a gas. This force is why a piece of wood floats on water, a helium balloon rises in the air, or you feel lighter when you’re in a swimming pool.

This phenomenon occurs because pressure in a fluid increases with depth. The bottom of an immersed object experiences a greater fluid pressure than its top. The difference in these pressures creates a net upward force, which we call upthrust.

An Experiment to Demonstrate the Existence of Upthrust

This simple experiment uses common lab equipment to clearly show that a fluid pushes upwards on an object.

Aim: To demonstrate that a fluid (water) exerts an upward force (upthrust) on an object placed in it.

Materials Required:

1. A spring balance (or a digital force meter)
2. A small, dense object (e.g., a metal weight or a stone)
3. A beaker or a large overflow can
4. Water
5. A thin string or thread

Procedure:

1. Setup: Tie the metal weight securely to the hook of the spring balance using the string. Hold the spring balance from the top so that the object hangs freely in the air.
2. Measure Weight in Air: Carefully note the reading on the spring balance. This value represents the true weight of the object. Let’s call this reading W₁.
3. Prepare the Beaker: Fill the beaker with water until it is almost full. If you are using an overflow can, ensure the spout is clear.
4. Immerse the Object: Now, slowly lower the object suspended from the spring balance into the beaker of water. Ensure the object is completely submerged but does not touch the bottom or sides of the beaker.
5. Measure Weight in Water: Observe the new reading on the spring balance while the object is still submerged. You will immediately notice that the reading has decreased. Let’s call this new, lower reading W₂.

Observations:

• The spring balance reading in air (W₁) is greater than the reading when the object is submerged in water (W₂).
• This means the object appears to weigh less when it is inside the water.

Explanation and Conclusion:

The apparent loss in weight (W₁ – W₂) is not because the water is “erasing” mass. Instead, the water is exerting an upward force on the object, which counteracts some of the downward pull of gravity. This upward force is the upthrust.

The spring balance measures the net downward force. When the upthrust from the water pushes up, it supports some of the object’s weight, so the spring balance has to pull with less force to hold the object, resulting in a lower reading.

Question 2. 

In what direction and at what point does the buoyant force on a body due to a liquid act? 

Ans:

The buoyant force, often called upthrust, is the upward force exerted by a fluid (a liquid or a gas) that opposes the weight of an object immersed in it. To answer your question precisely:

Direction of the Buoyant Force

The buoyant force always acts vertically upward. This direction is independent of the shape of the object or how it is oriented in the fluid. It is directly opposite to the direction of the effective weight of the fluid, which is downward due to gravity.

Point of Action of the Buoyant Force

The buoyant force acts through a specific point called the Center of Buoyancy.

The Center of Buoyancy is defined as the center of mass of the fluid which would have been there if the object were not present. In simpler terms, it is the geometric center (the centroid) of the immersed portion of the body.

To visualize this:
Imagine you carefully mark the outline of the part of the object that is submerged in the liquid. Now, mentally remove the object and fill that exact submerged volume with the same liquid. The center of mass of that hypothetical, shaped volume of liquid is the center of buoyancy. The buoyant force acts vertically upward through this point.

A Key Distinction

It is crucial to understand that the center of buoyancy is not necessarily the same as the object’s own center of gravity. The center of gravity is a fixed property of the object’s mass distribution, while the center of buoyancy depends entirely on the shape of the submerged volume.

• For a completely and uniformly submerged object (like a sealed box underwater), the center of buoyancy is fixed and coincides with the object’s geometric center.
• For a floating or partially submerged object (like a ship), the center of buoyancy shifts as the object tilts or rolls, because the shape of the submerged volume changes. This shifting is what helps a stable object like a ship right itself.

Question 3.

What is meant by the term buoyancy? 

Ans:

At its simplest, buoyancy is the uplifting force, the invisible “lift,” that a fluid gives to an object that is placed in it. Think of the feeling you get when you try to push a beach ball underwater; that powerful push back against your hands is buoyancy at work.

This happens because of a fundamental difference in pressure. A fluid, which can be a liquid like water or a gas like air, has weight and exerts pressure on all sides of an object submerged within it. This pressure increases with depth. So, the bottom of a submerged object experiences a greater upward push from the fluid than the downward push on its top. This difference in pressure results in a net force that points upward. We call this net upward force the buoyant force.

The strength of this buoyant force is governed by a principle discovered by the ancient Greek thinker Archimedes. It states that the buoyant force on an object is equal to the weight of the fluid that the object displaces.

Imagine you carefully lower an object into a full bucket of water. The water that spills out over the edge has a specific weight. Archimedes’ principle tells us that the buoyant force pushing up on the object is exactly equal to the weight of that spilled water.

This is why some things float and others sink:

• An object floats if the buoyant force (weight of displaced fluid) is greater than the object’s own weight. A massive steel ship floats because its hollow shape displaces a huge volume of water, and the weight of that water is greater than the ship’s weight.
• An object sinks if its own weight is greater than the buoyant force it creates. A small, solid steel bolt sinks because it only displaces a little bit of water, and the weight of that water is less than the bolt’s weight.
• An object remains suspended (neutrally buoyant) when the two forces are perfectly balanced.

Question 4. 

Define upthrust and state its S.I. unit. 

Ans:

Upthrust is the upward force exerted on an object when it is fully or partially submerged in a fluid (a liquid or a gas). This force arises because the pressure in a fluid increases with depth. The pressure on the lower surface of the submerged object is greater than the pressure on its upper surface, resulting in a net upward push. The magnitude of this force is exactly equal to the weight of the fluid that the object displaces, a principle famously established by Archimedes.

For example, when you try to push an empty bucket underwater, you feel this upward push resisting you; that is the upthrust in action.

The S.I. The unit of upthrust is the newton (N). Since upthrust is a type of force, it shares the same standard unit of measurement.

Question 5. 

What is the cause of upthrust? At which point can it be considered to act? 

Ans:

The Cause of Upthrust

At its heart, upthrust (also known as buoyant force) is caused by a simple imbalance of pressure in a fluid (a liquid or a gas). Here’s a step-by-step breakdown of how this works:

1. Pressure Increases with Depth: In any fluid, the pressure is not the same at all levels. The deeper you go, the greater the weight of the fluid above, and therefore the higher the pressure. An object submerged in a fluid experiences greater pressure on its lower surfaces than on its upper surfaces.
2. The Force from Below is Stronger: Imagine a cube submerged in water. The water pushes against every face of the cube. The force pushing down on the top of the cube is less than the force pushing up on the bottom of the cube because the bottom is at a greater depth and experiences higher pressure.
3. The Net Result is an Upward Push: When you add up all these pressure forces from the fluid, the horizontal forces cancel each other out. However, the upward force on the bottom is greater than the downward force on the top. This difference in forces results in a single, net force that acts in the upward direction. This net force is what we call upthrust or buoyancy.

In essence, the fluid is constantly “trying” to push the object upwards because it cannot exert an equal force on all sides due to the pressure gradient caused by gravity.

The Point Where Upthrust is Considered to Act

Upthrust can be considered to act through a single, specific point called the Center of Buoyancy.

• Definition: The Center of Buoyancy is the center of mass of the fluid that the object displaces.
• How to Visualize It: Imagine you magically remove the submerged object and fill the exact space it occupied with the same fluid. The center of mass of that newly-filled, shaped volume of fluid is the center of buoyancy.
• Why This Point? The forces of pressure from the fluid act all over the submerged surface of the object. For the purpose of calculating overall motion and stability, we can simplify this complex distribution of forces into a single, resultant force (the upthrust) acting straight upwards through this one point.

A Practical Example:
Think of a ship. The center of buoyancy is located within the submerged part of the ship’s hull. For the ship to be stable, this center of buoyancy must be positioned correctly relative to the ship’s own center of gravity. If you were to tilt the ship, the center of buoyancy would shift, creating a force that tries to right the ship again.

Question 6. 

Why is a force needed to keep a block of wood inside water? 

Ans:

It seems strange at first, doesn’t it? If you let a block of wood go above water, it bobs right to the surface. To keep it fully underwater, you have to push down on it. The reason for this isn’t that the wood is “afraid of water,” but rather the result of a constant, invisible tug-of-war between two forces.

The key player here is a force called the buoyant force. You can think of it as a kind of “water lift.” When you submerge the wood, it displaces, or pushes aside, a certain volume of water. The surrounding water pushes back against this from all directions, but the push from the bottom is stronger than the push from the top because pressure increases with depth. This difference in pressure creates a net upward force—that’s the buoyant force.

Now, let’s look at the other team in this tug-of-war: gravity. Gravity is pulling the block of wood straight down towards the center of the Earth. We feel this as the wood’s weight.

Here’s the crucial part: the strength of the buoyant force depends on the weight of the water the block displaces. Wood is less dense than water, meaning for a block of wood and a bucket of water of the same size, the wood is lighter.

So, when the wood is fully submerged, it’s displacing a volume of water that is heavier than the wood itself. This means the upward buoyant force is actually stronger than the downward force of gravity (the wood’s weight).

If the upward force is stronger than the downward force, the object must move upward—and it does! That’s why it floats.

Therefore, to keep the block submerged and stationary, your hand must provide that missing downward force. You are essentially making up the difference. You are adding just enough extra downward pull to balance the powerful upward push of the water, so that the total downward force (gravity + your push) equals the upward buoyant force.

A Simple Summary:

Imagine the block of wood is a spring that is naturally stretched out. Pushing it underwater is like compressing that spring. The moment you let go, the spring (the buoyant force) pushes it back to its natural, resting position—the surface. Your hand is simply the clamp that holds the compressed spring in place.

Question 7. 

A piece of wood if left under water comes to the surface. Explain the reason. 

Ans:

We’ve all seen it happen: you try to push a piece of wood down into a pond or a bathtub, and the moment you let go, it pops right back up to the surface. This isn’t just a quirky trait of wood; it’s a classic demonstration of a fundamental force of nature.

The main reason for this is a simple battle of density.

Think of density as how much “stuff” is packed into a certain space. Water has a certain density. A piece of wood, by its very nature, is made of fibers and has tiny air pockets trapped inside it. This means that, on average, the same volume of wood is less dense than the same volume of water. It’s lighter for its size.

Now, imagine the wood is fully submerged. The water beneath it is pushing it upward with a force that is equal to the weight of the water the wood has “taken the place of.” This is the buoyant force. Since the wood is less dense, the water it displaces is actually heavier than the wood itself.

So, the upward push from the displaced water is stronger than the downward pull of the wood’s own weight. This net upward force is what we experience as buoyancy. The wood is literally being pushed to the surface by the water around it because it’s a lighter imposter in the water’s space.

It will keep rising until it reaches a point of balance. This is when part of the wood is above the surface. At this stage, the volume of water it’s still displacing (the part that is underwater) now has a weight exactly equal to the weight of the entire piece of wood. The forces are balanced, and it floats peacefully.

For a clear contrast, a stone is much denser than water. The weight of the water it displaces is less than its own weight, so the downward pull wins, and it sinks.

In short, wood floats because it is naturally less dense than water, causing the surrounding water to exert a stronger upward force than the wood’s own downward weight, pushing it to the surface until a perfect balance is found.

Question 8. 

Describe an experiment to show that a body immersed in a liquid appears lighter than it really is. 

Ans:

Experiment: Discovering the “Vanishing” Weight

Aim: To demonstrate that when a body is submerged in a liquid, it experiences an upward force that makes it appear lighter than its actual weight.

The Core Idea: Imagine lifting a heavy rock. Now, try lifting that same rock from the bottom of a swimming pool. It feels surprisingly easier! This experiment allows us to measure that “missing” weight and understand where it goes.

What You’ll Need:

• A spring balance (or a digital kitchen scale that can be suspended from a stand).
• A solid, non-absorbent object that is heavier than water and can be easily hung (e.g., a small metal weight, a stone tied with a string, or a dense piece of plastic).
• A transparent beaker or a tall measuring jug.
• Water.
• A strong string.
• A retort stand with a clamp (or any creative way to hang the spring balance securely over the beaker).

Step-by-Step Procedure:

1. The Setup: First, set up your retort stand and clamp. Hang the spring balance from it securely. Make sure the beaker is positioned directly underneath the balance, but empty for now.
2. Find the True Weight: Tie your chosen object (let’s say a stone) to the hook of the spring balance using the string. Allow it to hang freely in the air. Carefully note down the reading on the spring balance. This is the object’s true weight in air. Let’s call this reading W₁.
3. The Submersion: Now, slowly pour water into the beaker until the stone is completely submerged. Do not let the stone touch the bottom or sides of the beaker. It should be hanging freely in the middle of the water.
4. Observe the “Apparent Weight”: Look at the spring balance again. You will immediately see that the reading has decreased. Note down this new, lower reading. This is the object’s apparent weight in water. Let’s call this reading W₂.
5. Calculate the “Loss” of Weight: The difference between the two readings is the force that made the object appear lighter.
   • Loss in Weight = True Weight (W₁) – Apparent Weight (W₂)

A Dramatic Enhancement (The Overflow Can Demonstration):

To make this even more compelling, you can use a special container called an “overflow can.” This is a spouted beaker filled to the very brim with water.

• Repeat the setup, but place an empty, dry beaker under the spout of the overflow can.
• Submerge the stone. As it enters the water, it will displace its own volume of water, which will flow out of the spout and into the empty beaker.
• Now, carefully collect the displaced water from the beaker.
• Weigh this collected water. You will find something remarkable: The weight of the displaced water is exactly equal to the “loss in weight” (W₁ – W₂) you calculated earlier.

What You’ve Discovered:

The experiment clearly shows that a body immersed in a liquid experiences an upward push, known as the buoyant force. This force is responsible for the object appearing lighter. The enhanced part of the experiment proves a fundamental law of physics: The buoyant force is equal to the weight of the fluid displaced by the object. This is Archimedes’ Principle in action.

In essence, the liquid is actively pushing up against the object, counteracting gravity and creating the sensation of reduced weight. This is why ships float, swimmers feel buoyant, and that rock in the swimming pool is so much easier to lift.

Question 9. 

Will a body weigh more in air or vacuum when weighed with a spring balance? Give a reason for your answer. 

Ans:

The Reason: The Missing Buoyant Force

The reason for this is the absence of the buoyant force (or upthrust) exerted by air.

1. How a Spring Balance Works: A spring balance measures the actual force (tension) required to support an object. This is different from a beam balance, which compares masses.
2. The Effect of Air (Buoyancy): Every object immersed in a fluid (like air) experiences an upward buoyant force. This force is equal to the weight of the air displaced by the object, as stated by Archimedes’ principle.
   • When you weigh the body in air, the spring balance only has to provide enough force to counteract the difference between the object’s actual weight (directed downwards) and the buoyant force (directed upwards).
   • So, the reading on the balance is: True Weight – Buoyant Force.
3. The Effect of a Vacuum: In a vacuum, there is no surrounding air. Therefore, there is no buoyant force acting upwards on the object.
   • In this case, the spring balance must provide the full force to counteract the object’s true weight.
   • The reading on the balance is the full True Weight.

Question 10. 

A metal solid cylinder tied to a thread is hanging from the hook of a spring balance. The cylinder is gradually immersed into the water contained in a jar. What changes do you expect in the readings of the spring balance? Explain your answer. 

Ans:

The Changing Reading of the Spring Balance

When the metal cylinder is gradually immersed in water, the reading on the spring balance will decrease steadily until the cylinder is completely submerged. After full immersion, the reading will stabilize and remain constant, regardless of how much deeper it is pushed.

Here is a step-by-step explanation of why this happens:

1. The Starting Point: Cylinder in Air

Initially, the cylinder hangs freely in the air. The spring balance measures the total downward force, which is simply the weight of the cylinder (mass × acceleration due to gravity). At this point, the reading is at its maximum.

2. The Gradual Immersion: The Role of Buoyancy

As the cylinder is lowered into the water, it starts to displace a volume of water equal to the volume of the part of the cylinder that is submerged. This is where Archimedes’ Principle comes into play.

This principle states that an object immersed in a fluid (liquid or gas) experiences an upward buoyant force. The magnitude of this force is exactly equal to the weight of the fluid displaced by the object.

• Buoyant Force = Weight of Displaced Water

This buoyant force acts in the upward direction, directly opposing the downward force of gravity (the weight).

3. The Net Force and the Spring Balance Reading

The spring balance does not measure just the weight; it measures the tension in the thread, which is the net force acting on the cylinder.

• Tension in Thread = Weight of Cylinder (downwards) – Buoyant Force (upwards)

As more of the cylinder is immersed, the volume of water it displaces increases. A greater displaced volume means a greater buoyant force.

Since the weight of the cylinder remains constant, a larger buoyant force means a smaller net downward force (tension). Therefore, the spring balance shows a steadily decreasing reading as immersion progresses.

4. The Point of Full Submersion: A Constant Reading

The critical moment occurs when the entire cylinder is just completely under the water surface. At this point, it cannot displace any more water than its own total volume.

• Once fully submerged, the volume of displaced water becomes constant (equal to the total volume of the cylinder).
• Therefore, the buoyant force also becomes constant.
• With both the weight and the buoyant force now constant, the net force (Tension) also becomes constant.

Pushing the cylinder deeper will not change the reading because the volume of water displaced remains the same.

Question 11. 

A body dipped into a liquid experiences an upthrust. State two factors on which upthrust on the body depends. 

Ans:

A body dipped into a liquid experiences an upthrust. The two factors on which this upthrust depends are:

1. The density of the liquid in which the body is immersed. A denser liquid, like salt water, will exert a greater upthrust on the same body compared to a less dense liquid, like fresh water.
2. The volume of the body that is submerged in the liquid. A larger submerged portion of the body will displace a greater amount of liquid, resulting in a stronger upthrust force.

Question 12. 

How is the upthrust related to the volume of the body submerged in a liquid? 

Ans:

Imagine pushing an empty, sealed plastic container into a bucket of water. The deeper you push it, the more forcefully it tries to pop back up. That upward force you feel is the upthrust, also known as the buoyant force. So, what’s really going on here? The secret lies in the amount of water your container is displacing.

The fundamental principle at work is Archimedes’ principle, which states that the upthrust on an object submerged in a fluid is equal to the weight of the fluid the object displaces.

Now, let’s connect this to volume. The weight of the displaced fluid is directly determined by its volume. We know that:

Weight = Mass × Gravity
and
Mass = Density × Volume

Combining these, we get: Weight of displaced liquid = Density of liquid × Volume displaced × Gravity

Since upthrust equals this weight, the formula becomes:

Upthrust = Density of liquid × Volume submerged × Gravity

This equation reveals the core relationship: The upthrust is directly proportional to the volume of the body submerged in the liquid.

Let’s break down what this means in practical terms:

• Direct Proportionality: If you double the submerged volume of an object, you double the amount of liquid it displaces. Doubling the displaced liquid means doubling its weight, and therefore, the upthrust also doubles. If you submerge only half the volume, you get only half the upthrust.
• Complete vs. Partial Submersion:
  • For an object that is completely submerged (like a rock sunk to the bottom of a pond), its entire volume is displacing liquid. Since the submerged volume cannot increase further, the upthrust remains constant no matter how deep it goes (assuming the liquid’s density is uniform).
  • For a floating object (like a ship or a swimming person), the submerged volume is only a part of the total object’s volume. As the object settles, it submeres just enough volume so that the upthrust exactly equals its own total weight. A heavier ship sinks deeper, increasing its submerged volume to generate a greater upthrust to balance its weight.

A Simple Thought Experiment:

Think of two identical balloons, one fully inflated and the other only half-inflated. If you push both completely under water, the fully inflated balloon has a much larger volume submerged. It will experience a much stronger push upwards because it displaces a much greater weight of water.

Question 13. 

A bunch of feathers and a stone of the same mass are released simultaneously in air. Which will fall faster and why? How will your observation be different if they are released simultaneously in vacuum?

Ans:

In Air: The Stone Falls Faster

When released in air, the stone will fall and hit the ground significantly faster than the bunch of feathers.

Why?

The reason is air resistance. While gravity pulls both objects downward with the same force (because they have the same mass), the air pushes back against them with different amounts of force.

• The Stone: It is very dense and compact. Its small surface area means it has to push aside only a little bit of air as it falls. The upward force of air resistance acting on it is very small compared to the downward pull of gravity. Therefore, it accelerates quickly and reaches a high speed.
• The Bunch of Feathers: It has a very large and irregular surface area. As it falls, it has to push aside a huge amount of air. This creates a very large upward force of air resistance. This force almost immediately balances out the downward force of gravity, causing the feathers to reach a very low terminal velocity very quickly and then float down slowly.

Think of it like this: The stone is like a sleek diver entering water, while the feathers are like an open parachute. The parachute is designed to maximize air resistance, which is exactly what the feathers do naturally.

In Vacuum: They Fall at the Exact Same Speed

If you could perform this experiment inside a vacuum chamber (a space with all the air removed), the observation would be completely different. Both the feathers and the stone would fall at the exact same rate and hit the ground at the exact same time.

Why?

In a vacuum, there is no air. Therefore, the factor that was holding the feathers back—air resistance—is completely eliminated. Since they have the same mass, gravity pulls them with the same force, causing them to accelerate downwards at the same rate (approximately 9.8 m/s² on Earth).

This demonstrates a fundamental principle of physics first proposed by Galileo: all objects, regardless of their mass or composition, will fall with the same acceleration in the absence of air resistance. The mass of the object does not affect its rate of fall because a more massive object is both harder to accelerate (has more inertia) and is pulled by a stronger gravitational force; these two effects cancel each other out perfectly.

Question 14. 

A body experiences an upthrust F1 in river water and F2 in sea water when dipped up to the same level. Which is more, F1 or F2? Give a reason. 

Ans:

When an object is submerged to an equal depth in two different liquids, the buoyant force acting on it, also known as upthrust, varies. In this case, the upthrust in sea water (F2) is greater than the upthrust in river water (F1).

This difference occurs due to the fundamental principle of buoyancy, established by Archimedes. The principle states that any object, either partially or entirely immersed in a fluid, is acted upon by an upward force equivalent to the weight of the fluid it displaces.

This relationship is expressed by the formula:
Upthrust = Volume of displaced fluid × Density of the fluid × Acceleration due to gravity

Since the object is dipped to the same level in both river water and sea water, the volume of fluid displaced remains constant. The acceleration due to gravity is also a constant factor in this scenario.

Consequently, the density of the fluid becomes the sole determining variable for the magnitude of the upthrust. Sea water possesses a higher density because it contains a substantial concentration of dissolved salts and minerals. In contrast, river water is fresh water and has a comparatively lower density due to the minimal presence of these dissolved substances.

Because the density of sea water is greater than that of river water, and the displaced volume is identical, the weight of the sea water displaced is also greater. It follows that the upward force experienced by the object in the denser sea water, F2, is stronger than the force F1 experienced in the less dense river water.

Question 15. 

A small block of wood is completely immersed in (i) water, (ii) glycerine and then released. In each case, what do you observe? Explain the difference in your observation in the two cases. 

Ans:

(i) When immersed in water and released:

You would observe that the small block of wood, after being released, initially moves upwards quickly. It shoots through the water, breaks the surface, and then bobs for a moment before coming to rest floating with a significant part of its volume above the water surface. Only a portion of the block remains submerged.

(ii) When immersed in glycerine and released:

In this case, the block of wood would also move upwards when released, but its motion would be noticeably slower and more sluggish compared to its movement in water. It will still break the surface and float, but it will settle such that a much larger portion of its volume remains submerged below the glycerine surface. It sits lower in the glycerine compared to in water.

Explanation of the Difference in Observation:

1. The difference in these two behaviors stems from a difference in the density of the two liquids.
2. The Principle of Buoyancy: According to Archimedes’ principle, when an object is placed in a fluid, it experiences an upward buoyant force. An object will float if this buoyant force is greater than or equal to the object’s own weight.
3. The Role of Density: The wood has a density less than both water and glycerine, which is why it floats in both. However, glycerine is significantly denser and heavier than water.

• Why the Block Floats Higher in Water:

In water, the wood must displace a certain volume of water to generate a buoyant force equal to its weight. Since water is less dense, a relatively large volume of it needs to be displaced to match the wood’s weight. This results in a significant part of the wooden block rising above the surface to achieve this balance, leaving a smaller portion submerged.

• Why the Block Floats Lower in Glycerine:

Because glycerine is denser, a much smaller volume of it has the same weight. Therefore, the wooden block only needs to displace a small volume of glycerine to create a buoyant force equal to its own weight. To displace this smaller volume, a larger portion of the block’s volume must remain submerged. Consequently, it floats much lower in the glycerine.

A Simple Analogy: Imagine you need to lift a 1 kg weight. If you use light, fluffy feathers, you would need a very large basketful of them to weigh 1 kg. But if you use lead shot, you would only need a small cupful to reach 1 kg. The wood is like the “container,” and it only needs to “hold” a small volume of the “heavy” fluid (glycerine) or a large volume of the “light” fluid (water) to achieve the same “weight” (buoyant force).

Question 16. 

A body of volume V and density ρ is kept completely immersed in a liquid of density ρL. If g is the acceleration due to gravity, then write expressions for the following:

(i) The weight of the body, (ii) The upthrust on the body,

(iii) The apparent weight of the body in liquid, (iv) The loss in weight of the body. 

Ans:

Taking g as the acceleration due to gravity, the required expressions are as follows:

(i) The weight of the body
The weight of a body is the force of gravity acting on it, given by the product of its mass and gravitational acceleration. Since mass (m) = density (ρ) × volume (V), the expression is:
Weight = ρVg

(ii) The upthrust on the body
The upthrust, or buoyant force, is equal to the weight of the liquid displaced by the body. As the body is completely immersed, the volume of liquid displaced is equal to the volume of the body (V). The mass of the displaced liquid is ρ_LV, so the upthrust is:
Upthrust = ρ_LVg

(iii)
The apparent weight is the measured weight of the body when it is submerged. It is equal to the actual weight minus the upthrust force. Therefore, the expression is:
Apparent Weight = Weight – Upthrust = ρVg – ρ_LVg = Vg(ρ – ρ_L)

(iv) The loss in weight of the body
The loss in weight is the difference between the weight of the body in air and its apparent weight in the liquid. This difference is numerically equal to the upthrust acting on it.
Loss in Weight = Weight – Apparent Weight = Upthrust = ρ_LVg

Question 17. 

A body held completely immersed inside a liquid experiences two forces:

(i) F1, the force due to gravity and

(ii) F2, the buoyant force.

Draw a diagram showing the direction of these forces acting on the body and state the condition when the body will float or sink.

Ans:

Diagram Description

Imagine a simple, solid cube completely submerged in a liquid, contained within a beaker.

• Force F1 (Force due to Gravity): This is the weight of the body. It is represented by a vertical arrow pointing downwards, starting from the center of the cube. This arrow is labeled F₁.
• Force F2 (Buoyant Force): This is the upward force exerted by the liquid. It is represented by a vertical arrow pointing upwards, also starting from the center of the cube. This arrow is slightly longer than F1 to visually represent a case where the body might rise, and it is labeled F₂.

(Since I cannot create an image, please draw this based on the description above. The key is that both forces act through the center of the body but in opposite directions.)

Condition for the Body to Sink or Float

The motion of the body is determined by the relative magnitudes of these two forces.

1. Condition for Sinking:
The body will sink if the downward force due to gravity is greater than the upward buoyant force.
In other words:
F₁ > F₂

This happens when the density of the body is greater than the density of the liquid it is immersed in. Its weight is simply too great for the buoyant force to support.

2. Condition for Floating:
The body will float if the upward buoyant force is greater than or equal to the downward force due to gravity.
In other words:
F₂ ≥ F₁

More precisely:

• If F₂ > F₁, the body will accelerate upwards and rise to the surface. Once it reaches the surface, it will float partially immersed until the buoyant force from the displaced liquid equals its weight (F₂ = F₁).
• If F₂ = F₁ right from the start, the body will remain in equilibrium at any submerged depth. This means the density of the body is equal to the density of the liquid.

Question 18. 

1. Complete the following sentence : Two balls, one of iron and the other of aluminium experience the same upthrust when dipped completely in water if _____________ .

2. Complete the following sentence : An empty tin container with its mouth closed has an average density equal to that of a liquid. The container is taken 2 m below the surface of that liquid and is left there. Then the container will ____________ .

3. Complete the following sentence : A piece of wood is held under water. The upthrust on it will be ___________  the weight of the wood piece. 

Ans:

1. Two balls, one of iron and the other of aluminium, experience the same upthrust when dipped completely in water if their volumes are equal.

Reasoning: The buoyant force acting on an object submerged in a fluid is determined by the amount of fluid it displaces, not by the object’s own material composition. This is the essence of Archimedes’ principle. Since both balls are fully immersed and have identical volumes, they push aside the exact same amount of water. The water exerts an upward force equal to the weight of this displaced volume. Whether that space is occupied by dense iron or lighter aluminium is irrelevant to the water; the reaction force depends solely on the volume of water moved. Consequently, the upward push, or upthrust, is identical for both spheres.

2. An empty tin container with its mouth closed has an average density equal to that of a liquid. The container is taken 2 m below the surface of that liquid and is left there. Then the container will remain at rest at that location.

Reasoning: An object will achieve a state of neutral buoyancy—neither sinking nor rising—when its overall density matches that of the surrounding fluid. In this case, the container’s density is equal to the liquid’s density. This balance means the downward force of gravity on the container is exactly countered by the upward buoyant force from the displaced liquid. With these two opposing forces cancelling each other out, the net force on the container is zero. According to fundamental physics, an object with no net force acting upon it will not accelerate. Therefore, the container has no tendency to move and will remain stationary at the 2-meter depth where it was released.

3. A piece of wood is held under water. The upthrust on it will be greater than the weight of the wood piece.

Reasoning: Wood is naturally less dense than water, which is why it floats. When floating freely, it settles so that the portion below the surface displaces a volume of water whose weight equals the wood’s entire weight. However, when the wood is pushed and held completely underwater, it is forced to displace a volume of water equal to its own total volume. This total volume is greater than the submerged volume it has when floating. Since the upthrust equals the weight of the actual displaced water, this force becomes greater than the wood’s weight. This is the reason you must apply a continuous downward force to keep it submerged; you are counteracting this excess buoyant force that wants to push the wood back to the surface.

Question 19. 

Prove that the loss in weight of a body when immersed wholly or partially in a liquid is equal to the buoyant force (or upthrust) and this loss is because of the difference in pressure exerted by liquid on the upper and lower surfaces of the submerged part of body. 

Ans:

Proof of Archimedes’ Principle Based on Fluid Pressure

The observation that a body immersed in a fluid experiences an upward force, leading to an apparent loss of weight, is a fundamental concept in fluid mechanics. This can be rigorously proven by examining the forces exerted by the fluid pressure on the submerged body.

Part 1: Establishing the Scenario

Consider a solid body of an arbitrary shape submerged in a fluid of density (ρ). To analyze the forces, we will use a thought experiment involving a simpler object.

Imagine a right circular cylinder with a cross-sectional area (A) and height (h) submerged in the fluid such that its top and bottom faces are horizontal. The top face is at a depth of (h₁) below the free surface of the fluid, and the bottom face is at a depth of (h₂). Therefore, the height of the cylinder is (h = h₂ – h₁).

Part 2: Analyzing the Forces Due to Fluid Pressure

The fluid pressure at any depth is given by (P = P₀ + ρgh), where (P₀) is the atmospheric pressure.

• Force on the Top Face:
  • Pressure at the top face, (P₁ = P₀ + ρgh₁)
  • This force acts downward (perpendicular to the surface).
  • Force (F₁) = Pressure × Area = (P₁ × A) = (P₀ + ρgh₁)A
• Force on the Bottom Face:
  • Pressure at the bottom face, (P₂ = P₀ + ρgh₂)
  • This force acts upward.
  • Force (F₂) = Pressure × Area = (P₂ × A) = (P₀ + ρgh₂)A
• Forces on the Side Walls:
  • The horizontal forces on the vertical side walls are equal and opposite at every point at the same depth. Therefore, they cancel each other out completely, resulting in no net horizontal force.

Part 3: Calculating the Net Vertical Force (Buoyant Force)

The net force acting on the cylinder is the vector sum of all the forces. Since the horizontal forces cancel, we only consider the vertical forces.

The downward force is (F₁) and the upward force is (F₂). Therefore, the net upward force (F_b), known as the buoyant force or upthrust, is:

(F_b = F₂ – F₁)
(F_b = [ (P₀ + ρgh₂)A ] – [ (P₀ + ρgh₁)A ])
(F_b = P₀A + ρgh₂A – P₀A – ρgh₁A)
(F_b = ρgA (h₂ – h₁))

Since (h₂ – h₁ = h), the height of the cylinder, we get:
(F_b = ρg A h)

Now, note that (A × h) is the volume of the cylinder, which is equal to the volume of the fluid displaced by the cylinder, (V_d).

Therefore,
F_b = ρg V_d

But (ρ × V_d) is the mass of the fluid displaced, and (ρg V_d) is the weight of the fluid displaced.

Hence, we have shown that:
Buoyant Force (F_b) = Weight of the fluid displaced by the object.

This is the formal statement of Archimedes’ principle.

Part 4: Connecting to Loss of Weight and Pressure Difference

1. Loss in Weight: When the cylinder is suspended in the fluid, two main vertical forces act on it:
   • Its actual weight (W_actual = mg) acting downward.
   • The buoyant force (F_b) acting upward.
     The net force measured by a scale (the apparent weight, W_apparent) is:
     (W_apparent = W_actual – F_b)
     Therefore, the loss in weight is (W_actual – W_apparent = F_b).
     This proves that the loss in weight is numerically equal to the buoyant force.
2. Origin in Pressure Difference: As derived in the calculation, the buoyant force (F_b) arose directly from the difference between the upward pressure on the bottom surface and the downward pressure on the top surface.
   (F_b = F₂ – F₁ = (P₂ – P₁) × A)
   Since (P₂ > P₁) because (h₂ > h₁), the net force is upward. The pressure difference is itself due to the difference in depth (h) and is equal to (ρgh). Thus, the loss in weight is fundamentally because of the difference in pressure exerted by the liquid on the upper and lower surfaces of the submerged part of the body.

Part 5: Generalization to an Arbitrary Shape

While we used a cylinder for simplicity, the principle holds for any shape. Any arbitrarily shaped body can be thought of as being composed of many tiny vertical columns similar to the one analyzed. For each column, the net vertical force is (ρg × volume of the column). The sum of the forces on all these columns is (ρg × total volume of the body), which is the weight of the fluid displaced by the entire body. The horizontal components on the slanted surfaces will always cancel out for the entire object, leaving only a net upward vertical force.

Conclusion

We have proven that for a body immersed in a fluid:

1. The loss of weight is exactly equal to the buoyant force (upthrust).
2. This buoyant force is numerically equal to the weight of the fluid displaced by the body.

Question 20. 

A sphere of iron and another sphere of wood of the same radius are held under water. Compare the upthrust on the two spheres.

[Hint: Both have equal volume inside the water].

Ans:

Imagine you have two boxes that are completely identical in size and shape. You fill one with feathers and the other with rocks. Even though the boxes hold the same amount of space, the rock-filled box is obviously much harder to lift. This same basic idea is the key to understanding what happens in water.

Since the two spheres have the same radius, they take up precisely the same amount of space; they have equal volume. The critical difference lies in how much “stuff,” or mass, is packed into that space.

Iron is a very heavy, compact material. A sphere made of it packs a tremendous amount of mass into its volume. In contrast, wood is made of a fibrous, porous material, so a sphere of the same size contains far less mass.

Now, think about what happens when you place an object in water. The water pushes back with a force that is directly related to the amount of water the object displaces. Because the spheres are the same size, the water pushes upward on both of them with an identical force.

This is where the balance tips. For the wooden sphere, the upward push from the water is stronger than the downward pull of the sphere’s own weight. As a result, it is buoyed to the surface and floats.

For the iron sphere, its weight is so immense—because it is so densely packed with mass—that the water’s upward push is simply not enough to hold it. The downward force wins, and the sphere sinks.

Ultimately, it comes down to a simple contest of forces. The water provides a fixed amount of lift for an object of that size. The wooden sphere is light enough to be supported, while the iron sphere is too heavy for that same lift to manage.

Question 21. 

A sphere of iron and another of wood, both of same radius are placed on the surface of water. State which of the two will sink? Give a reason for your answer. 

Ans:

It all comes down to a simple but powerful contest: the object’s weight pulling it down versus the water’s push holding it up. Even though two spheres are the same size, what they are made of decides the winner of this contest.

Since the spheres share the same radius, they take up precisely the same amount of space. Imagine two identical boxes; one is filled with feathers and the other with rocks. They are the same size, but their contents make one incredibly heavy and the other very light. This is the situation with the iron and wood spheres.

Iron is an inherently heavy, compact material for its size. A sphere of it is very massive. Wood, on the other hand, is light and porous. A sphere of wood of the exact same dimensions has far less mass.

Water has a natural “lifting power.” When you place an object in water, the water tries to hold it up with a force equal to the weight of the water the object displaces. Since our spheres are the same size, they displace the same amount of water, so the water’s lifting push is identical for both.

For the wooden sphere, this upward push from the water is more than enough to support its light weight, so it floats comfortably on the surface. For the iron sphere, its own weight is so much greater than the water’s maximum lifting effort that it wins the contest outright, and the sphere sinks straight to the bottom. In essence, the iron sphere is just too heavy for the amount of water it pushes aside, while the wooden sphere is light enough to be supported.

Question 22. 

How does the density of material of a body determine whether it will float or sink in water? 

Ans:

What Makes Something Float? It’s All About the Squeeze

We’ve all seen it: a heavy log drifts on a lake while a tiny pebble plummets to the bottom. It seems to defy common sense. The secret isn’t just about weight, but about how tightly packed that weight is. Scientists call this concept density.

A material like lead has a lot of mass crammed into a small box, making it very dense. A material like balsa wood has very little mass in that same box, making it low density.

Here’s the golden rule: An object will float if its material is less dense than the fluid it’s placed in. It will sink if its material is more dense.

Water acts as the benchmark. If an object’s material is “lighter” than water for the same amount of space, it floats. If it’s “heavier,” it sinks.

The Invisible Tug-of-War

To truly get it, picture an invisible battle of forces happening the moment an object touches the water.

1. The Downward Pull (Gravity): This is the force you’re most familiar with. It’s the weight of the object itself, pulling it straight down toward the Earth. The more mass the object has, the stronger this pull.
2. The Upward Push (The Water’s Pushback): This is the magic force. When an object enters water, it has to push some water out of the way to make space for itself. The water doesn’t like this and pushes back with a force equal to the weight of the displaced water. This is the floating force.

The winner of this tug-of-war decides the object’s fate.

• If the upward push is stronger, the object is forced to the surface and floats.
• If the downward pull is stronger, the object wins and sinks.

Connecting Density to the Battle

This is where it all comes together. Let’s compare two objects of the exact same size—a block of wood and a block of iron.

• The Wood Block: Wood is less dense than water. For its size, it’s relatively light. When it slides into the water, it displaces a volume of water that actually weighs more than the block itself. So, the upward push from the water is stronger than the downward pull of the block’s weight. It floats to the top.
• The Iron Block: Iron is much denser than water. For that same size, it’s incredibly heavy. When it enters the water, the weight of the water it displaces is far less than the weight of the block. The downward pull easily overpowers the upward push, and the block sinks.

The Shape-Shifter Trick: How Heavy Ships Float

This leads to the classic puzzle: “Steel is denser than water, so how does a 500-meter-long ship made of steel float?”

The answer is all about average density. A ship isn’t a solid block of metal; it’s a carefully shaped hollow container filled mostly with air.

While the steel itself is dense, the ship encloses a massive volume of empty space. If you take the entire mass of the ship (the steel, cargo, everything) and divide it by the huge volume it occupies (including all the air inside), you get an average density. This average density is actually lower than that of water. The ship displaces a colossal amount of water, creating an upward push so powerful it can support the ship’s immense weight. A solid steel bar of the same weight, being much more compact, has a much higher average density and sinks immediately.

The Simple Takeaway

At its heart, floating is a contest of heaviness for a given space. Water sets a specific weight limit for every liter of its volume. An object that is less dense stays on top because, for the space it occupies, it’s lighter than the water it displaces. An object that is more dense falls through because it’s heavier. It’s this clever interplay between an object’s density and the water’s powerful pushback that keeps the mightiest vessels afloat.

Question 23. 

A body of density ρ is immersed in a liquid of density ρL. State the condition when the body will (i) float and (ii) sink in the liquid. 

Ans:

The behavior of a body immersed in a liquid depends on the average density of the body (ρ) relative to the density of the liquid (ρL). The key principle at play is Archimedes’ principle, which states that the buoyant force acting on the body is equal to the weight of the liquid it displaces.

(i) Condition for the body to float:

The body will float when the average density of the body is less than or equal to the density of the liquid (ρ ≤ ρL).

This can be broken down into two scenarios:

• If ρ < ρL, the body will float partially immersed. It will rise and remain at the surface with a portion of its volume above the liquid. In this state, the weight of the liquid displaced by the submerged part is exactly equal to the weight of the entire body.
• If ρ = ρL, the body will float in a state of neutral equilibrium. It will remain at rest completely submerged at any depth within the liquid, as its weight is exactly balanced by the buoyant force.

(ii) Condition for the body to sink:

The body will sink when the average density of the body is greater than the density of the liquid (ρ > ρL).

In this case, the weight of the body is greater than the maximum possible buoyant force (which is the weight of the liquid displaced by the body’s entire volume). Since the downward force (weight) is greater than the upward force (buoyancy), the body experiences a net downward force, causing it to accelerate and sink to the bottom.

Question 24. 

It is easier to lift a heavy stone under water than in air. Explain.

Ans:

The experience of a stone feeling lighter when submerged is due to a supporting force provided by the water itself, known as buoyancy. To understand this, we need to consider the forces at play in both air and water.

When you lift a stone in air, you are fighting against a single, dominant force: the downward pull of gravity, which is the stone’s weight. The air, being a gas, is not dense enough to provide any significant upward push to counter this weight. Its effect is so minimal that we disregard it.

The situation changes completely when the stone is underwater. While the stone’s weight due to gravity remains the same, it now must displace, or push aside, a volume of water to make space for itself. The water, being a dense fluid, resists being pushed aside and pushes back against the stone from all directions.

The critical point is that the pressure from the water is greater at the bottom of the stone than at the top because the deeper you go, the greater the water pressure. This difference in pressure results in a net upward force acting on the stone—this is the buoyant force.

Essentially, when you lift the submerged stone, you are no longer lifting its full weight alone. The water is helping you by providing this upward buoyant force. You are only responsible for lifting the stone’s “apparent weight,” which is its true weight minus the weight of the water it displaced. Since a stone is denser than water, it still sinks, but the water’s upward support makes the task of lifting it feel significantly easier. The water is literally helping to hold the stone up.

Question 25. 

State the Archimedes’ principle. 

Ans:

The behavior of objects immersed in fluids is governed by a fundamental rule discovered long ago. Whether an object floats or sinks is determined not just by its own weight, but by a supportive interaction with the surrounding liquid or gas.

When an item is placed into a fluid, it inevitably occupies space, pushing the fluid out of the way. This displaced volume of fluid is the key to the upward lift, or buoyancy, that the object encounters. The strength of this lifting force is precisely equivalent to the gravitational weight of the fluid that was moved aside. In essence, the fluid “pushes back” with a force equal to what that displaced volume would have weighed.

This concept clarifies how massive, ocean-going vessels stay afloat. A ship’s hull is engineered to be largely hollow, shaping a volume that can displace a tremendous amount of water. The weight of this displaced water creates a powerful upward push that counteracts the ship’s own substantial weight, allowing it to float. On the other hand, a small, solid object like a stone displaces only a minimal volume of water. The resulting buoyant force is a weak upward push, easily overpowered by the stone’s own downward weight, causing it to sink.

Question 26. 

Describe an experiment to verify the Archimedes’ principle.

Ans:

Verifying Archimedes’ Principle: The Overflow Can Experiment

Objective: To demonstrate that when an object is submerged in a fluid, it experiences an upward buoyant force equal to the weight of the fluid it displaces.

The Core Idea: Archimedes’ principle can feel abstract. This experiment makes it tangible by directly comparing two key measurements:

1. The weight of the fluid displaced by the object.
2. The apparent loss of weight of the object when submerged (the buoyant force).

If these two values are equal, the principle is verified.

Materials Required:

• Overflow Can (Eureka Can): A specialized container with a spout designed to channel all displaced water into another vessel. A large beaker with a bent tube stuck through a stopper also works.
• Small, dense object: A metal weight or a stone that can be easily suspended. It should be insoluble in water.
• A spring balance or a digital scale: Sensitive enough to measure the small changes in weight.
• A small, lightweight beaker or a cup.
• A tripod stand or a support to hold the overflow can steady (optional, but helpful).
• Water
• A cloth or paper towels for spills.

Experimental Procedure:

Step 1: The Dry Run – Measuring True Weight

1. Suspend the object (e.g., the metal weight) from the hook of the spring balance.
2. Record its weight in the air. Let’s call this value W₁. This is the true weight of the object.

Step 2: Preparing the Can – The “Full” Mark

1. Place the overflow can on a flat surface, with the empty beaker under its spout.
2. Slowly pour water into the can until it begins to trickle out of the spout. Wait until the dripping stops completely.
3. At this point, remove the beaker (which now contains a small amount of initial overflow) and replace it with your clean, dry, lightweight beaker. The can is now perfectly full and ready.

Step 3: The Submersion – Catching the Displaced Water

1. Carefully hold the object suspended from the spring balance over the overflow can, ensuring it is not yet touching the water.
2. Gently lower the object until it is completely submerged in the water. Do not let it touch the bottom or sides of the can.
3. As the object enters the water, it will displace a volume of water equal to its own volume. This water will flow out through the spout and be collected in the small beaker.
4. Once the water stops dripping from the spout, take two readings:
   • Read the new weight shown on the spring balance. This is the apparent weight of the object in water. Let’s call this value W₂.
   • The buoyant force (B) acting on the object is the weight it has lost: B = W₁ – W₂.

Step 4: The Crucial Weigh-In – Measuring the Displaced Fluid

1. Carefully remove the beaker from under the spout, trying not to spill any of the displaced water it has collected.
2. Weigh the beaker with the displaced water inside it. Record this mass.
3. Now, empty the beaker, dry it thoroughly, and weigh it again to find its empty mass.
4. The weight of the displaced water (W_d) is the difference between these two masses, converted to Newtons (if using a scale that measures in grams, multiply the mass in kg by 9.8 m/s² to get weight in Newtons).

Observations and Calculations:

You will now have two key values:

• Buoyant Force (B) = W₁ – W₂
• Weight of Displaced Water (W_d)

Verification and Conclusion:

Compare the calculated buoyant force (B) with the measured weight of the displaced water (W_d).

If Archimedes’ principle is correct, these two values should be very nearly equal.

Within the limits of experimental error (like a tiny water spill, the precision of your scale, or a droplet left in the spout), B ≈ W_d.

This direct, one-to-one relationship confirms that the upward push you feel when lifting a rock in a pond isn’t magic—it’s a force precisely equal to the weight of the water your rock is pushing aside. This is the essence of Archimedes’ principle, and it’s the fundamental reason why steel ships float and hot air balloons rise.

Exercise 5 (A)

Question 1. 

A body will experience minimum upthrust when it is completely immersed in : 

1. Turpentine  
2. Water
3. Glycerine   
4. Mercury

Question 2. 

The S.I. unit of upthrust is : 

1. Pa
2. N
3. kg
4. kg m2

Question 3. 

A body of density ρ sinks in a liquid of density ρL.  The densities ρ and ρL are related as :

1. ρ = ρL
2. ρ < ρL
3. ρ > ρL
4. Nothing can be said.

Exercise 5 (A)

Question 1. 

A body of volume 100 cm3 weighs 5 kgf in air. It is completely immersed in a liquid of density 1.8 × 103 kg m-3. Find: The upthrust due to liquid and The weight of the body in liquid. 

Ans:

Step 1: Understanding the Problem

We are given a solid object with a volume of 100 cm³. When weighed in air, it registers a weight of 5 kgf. We then immerse it completely in a liquid with a density of 1.8 × 10³ kg/m³. Our goal is to determine the new weight reading of the object when it is submerged in this liquid.

Step 2: Convert the Volume to Consistent Units

The density is provided in kg/m³, so we must convert the object’s volume to cubic meters (m³) for consistency.

100 cm³ = 100 × (10⁻² m)³ = 100 × 10⁻⁶ m³ = 1.0 × 10⁻⁴ m³.

Step 3: Calculate the Buoyant Force (Upthrust)

Archimedes’ principle tells us that the buoyant force acting on the object is equal to the weight of the fluid it displaces.

• Volume of liquid displaced: 1.0 × 10⁻⁴ m³ (equal to the object’s volume).
• Mass of liquid displaced: Volume × Density = (1.0 × 10⁻⁴ m³) × (1.8 × 10³ kg/m³) = 0.18 kg.
• Weight of liquid displaced (Buoyant Force): Since 1 kg has a weight of 1 kgf, the weight of the displaced liquid is 0.18 kgf.

Therefore, the upward buoyant force acting on the object is 0.18 kgf.

Step 4: Determine the Apparent Weight in the Liquid

The weight scale measures the net downward force. When submerged, the buoyant force supports some of the object’s weight, making it seem lighter.

The apparent weight in the liquid is the true weight (in air) minus the buoyant force.

Apparent Weight = Weight in Air – Buoyant Force
*Apparent Weight = 5.00 kgf – 0.18 kgf*
*Apparent Weight = 4.82 kgf*

Final Answer:

The weight of the body when immersed in the liquid is 4.82 kgf.

Question 2. 

A body weighs 450 gf in air and 310 gf when completely immersed in water. Find 

(i) The volume of the body, (ii) The loss in weight of the body, and (iii) The upthrust on the body. State the assumption made in part (i). 

Ans:

Question 3. 

You are provided with a hollow iron ball A of volume 15 cm3 and mass 12 g and a solid iron ball B of mass 12 g. Both are placed on the surface of water contained in a large tub. Find upthrust on each ball. Which ball will sink? Give a reason for your answer (Density of iron = 8.0 g cm-3)

Ans:

Step 1: Analyze the Two Balls

We have two iron balls placed on water:

• Ball A (Hollow): Mass = 12 g, Total Volume = 15 cm³
• Ball B (Solid): Mass = 12 g
• Density of Iron = 8.0 g/cm³
• Density of Water = 1.0 g/cm³

Step 2: Determine the Upthrust (Buoyant Force) on Each

The upward force, or upthrust, on an object in water is equal to the weight of the water it pushes aside.

For Hollow Ball A:
First, find its overall density:
Overall Density = Mass / Volume = 12 g / 15 cm³ = 0.8 g/cm³

Since its density (0.8 g/cm³) is less than water’s density (1.0 g/cm³), Ball A will float. A floating object displaces a volume of water whose weight equals its own weight.

Therefore, the upthrust on Ball A is equal to its total weight.
Upthrust on A = 12 g-wt

For Solid Ball B:
First, find its actual volume as a solid piece of iron:
Volume = Mass / Density = 12 g / 8.0 g/cm³ = 1.5 cm³

Since its density (8.0 g/cm³) is greater than water’s density (1.0 g/cm³), Ball B will sink. A sinking object is fully submerged, so the upthrust is based on its entire volume.

Upthrust = Density of Water × Volume of Ball × g
= (1.0 g/cm³) × (1.5 cm³) × g
Upthrust on B = 1.5 g-wt

Step 3: Identify Which Ball Sinks and the Reason

Ball B, the solid iron ball, will sink.

Reason:

• Ball A is hollow. The trapped air increases its total volume, making its overall density lower than water. The water can push it up with a force strong enough to support its weight, allowing it to float.
• Ball B is solid and compact. Its high density means it is too heavy for its size. The maximum upward push the water can provide when the ball is completely submerged (1.5 g-wt) is not enough to counter its own weight (12 g-wt). This net downward force causes it to sink.

Question 4. 

A solid of density 5000 kg m-3 weighs 0.5 kgf in air. It is completely immersed in water of density 1000 kg m-3. Calculate the apparent weight of the solid in water. 

Ans:

When an object is completely immersed in a fluid, it experiences a reduction in its perceived weight. This occurs because of an upward force, known as buoyancy, which counteracts the object’s own weight. The magnitude of this buoyant force is precisely equal to the weight of the fluid that the object pushes aside, or displaces.

Consider a solid object with a weight of 0.5 kilogram-force (kgf) measured in air. Since the unit kgf already incorporates the standard gravitational acceleration, a weight of 0.5 kgf directly indicates a mass of 0.5 kilograms.

The object’s volume can be determined from its mass and its density, which is given as 5000 kilograms per cubic meter (kg/m³). The volume (V) is found using the formula:

V = Mass / Density = 0.5 kg / 5000 kg/m³ = 0.0001 cubic meters

This calculated volume represents the amount of space the object occupies and, consequently, the volume of fluid it will displace when fully submerged. To find the buoyant force, we calculate the weight of this displaced water. Given that the density of water is 1000 kg/m³, the mass of the displaced water is:

Mass of displaced water = Density of water × Volume = 1000 kg/m³ × 0.0001 m³ = 0.1 kg

The weight of this water, and thus the buoyant force acting on the object, is 0.1 kgf.

The apparent weight of the object while submerged is the result of its actual weight being partially supported by the buoyant force. It is calculated by subtracting the buoyant force from the weight in air:

Apparent Weight in Water = Weight in Air – Buoyant Force
Apparent Weight in Water = 0.5 kgf – 0.1 kgf = 0.4 kgf

Question 5. 

Two spheres A and B, each of volume 100 cm3 is placed on water (density = 1.0 g cm−3). The sphere A is made of wood of density 0.3 g cm−3 and sphere B is made of iron of density 8.9 g cm−3.Find: The weight of each sphere, and The upthrust on each sphere. Which sphere will float? Give a reason.

Ans:

Analyzing the Wood and Iron Spheres

To understand how the wooden and iron spheres behave in water, we need to examine three key aspects: their individual weights, the upward buoyant force (upthrust) they experience, and how these forces determine whether they float or sink.

1. Calculating the Weight of Each Sphere

An object’s weight is the force of gravity pulling it downward. It is calculated by multiplying its density by its volume.

• Wooden Sphere (A):
  With a density of 0.3 g/cm³ and a volume of 100 cm³, its mass is 30 grams. Therefore, its weight is equivalent to the force exerted by a 30-gram mass.
• Iron Sphere (B):
  With a much higher density of 8.9 g/cm³ and the same 100 cm³ volume, its mass is 890 grams. Consequently, its weight is equivalent to the force exerted by an 890-gram mass.

Summary: The iron sphere is significantly heavier, with a weight nearly 30 times greater than that of the wooden sphere.

2. Determining the Upthrust on Each Sphere

Upthrust, or the buoyant force, is the upward push exerted by a fluid. According to Archimedes’ principle, this force equals the weight of the fluid displaced by the object. The maximum amount of water either sphere can displace is 100 cm³, which has a mass of 100 grams.

• Wooden Sphere (A):
  Since wood is less dense than water, this sphere will not sink completely. It will float, settling at a point where it has displaced just enough water to balance its own weight. Therefore, the upthrust acting on it will be exactly equal to its weight, which is equivalent to a 30-gram force.
• Iron Sphere (B):
  Iron is denser than water, so this sphere will sink and become fully submerged. It will displace the maximum possible volume of water (100 cm³). This results in the maximum possible upthrust, equivalent to a 100-gram force.

Summary: Despite its greater weight, the iron sphere only experiences an upthrust equivalent to 100 grams, while the wooden sphere, though lighter, is perfectly supported by a 30-gram upthrust.

3. Identifying Which Sphere Will Float

The key to flotation lies in the balance between weight (downward force) and maximum possible upthrust (upward force).

• Wooden Sphere (A): Floats
  Its weight is equivalent to a 30-gram force, while the maximum upthrust available is a 100-gram force. Because the maximum upward push is greater than the downward pull, the sphere will rise and adjust its position in the water. It will float, with part of its volume above the surface, until the upthrust exactly matches its weight.
• Iron Sphere (B): Sinks
  Its weight is equivalent to an 890-gram force, but the maximum upthrust it can generate is only a 100-gram force. The downward force is overwhelmingly greater than the maximum possible upward force. This net downward force causes the sphere to accelerate to the bottom.

The Fundamental Reason: A Matter of Density
Ultimately, this behavior boils down to a simple comparison of densities. An object will float if its average density is less than the density of the fluid it is placed in.

• The wooden sphere has a density (0.3 g/cm³) lower than water (1.0 g/cm³), so it floats.
• The iron sphere has a density (8.9 g/cm³) higher than water, so it sinks.

Question 6. 

The mass of a block made of certain material is 13.5 kg and its volume is 15 × 10-3 m3. (a) Calculate upthrust on the block if it is held fully immersed in water.

(b) Will the block float or sink in water when released? Give a reason for your answer.

(c) What will be the upthrust on the block while floating? Take density of water = 1000 kg m-3. 

Ans:

(a) Calculate the upthrust on the block if it is held fully immersed in water.

The upthrust (or buoyant force) on an object fully submerged in a fluid is given by Archimedes’ principle. It is equal to the weight of the fluid displaced by the object.

• Volume of the block, V = 15 × 10⁻³ m³
• Density of water, ρ_water = 1000 kg/m³
• Acceleration due to gravity, g = 9.8 m/s² (This is a standard value used unless specified otherwise)

Step 1: Calculate the mass of water displaced.
When fully immersed, the volume of water displaced is equal to the volume of the block.
Mass of water displaced = Density × Volume = ρ_water × V
= 1000 kg/m³ × (15 × 10⁻³ m³)
= 15 kg

Step 2: Calculate the weight of the water displaced (which is the upthrust).
Upthrust, F_b = Mass of water displaced × g
= 15 kg × 9.8 m/s²
= 147 N

Therefore, the upthrust on the block when fully immersed is 147 N.

(b) Will the block float or sink in water when released? Give a reason.

To determine if the block will float or sink, we compare its density to the density of water.

• Mass of the block, m_block = 13.5 kg
• Volume of the block, V_block = 15 × 10⁻³ m³

Step 1: Calculate the density of the block.
Density of block, ρ_block = Mass / Volume
= 13.5 kg / (15 × 10⁻³ m³)
= 900 kg/m³

Step 2: Compare densities.
Density of the block (ρ_block) = 900 kg/m³
Density of water (ρ_water) = 1000 kg/m³

Since the density of the block (900 kg/m³) is less than the density of water (1000 kg/m³), the block will float when released.

(c) What will be the upthrust on the block while floating?

When an object floats freely, it is in a state of equilibrium. The forces acting on it are balanced.

• The downward force is its weight (W = m_block × g).
• The upward force is the upthrust (F_b).

According to the principle of flotation, the weight of the floating body is equal to the weight of the liquid it displaces. Therefore, the upthrust must be equal to the weight of the block.

Step 1: Calculate the weight of the block.
Weight of block, W = m_block × g
= 13.5 kg × 9.8 m/s²
= 132.3 N

Step 2: Determine the upthrust.
Since the block is floating, Upthrust = Weight of the block
Therefore, the upthrust on the block while floating is 132.3 N.

Summary of Answers:

(a) Upthrust when fully immersed: 147 N
(b) The block will float because its density (900 kg/m³) is less than that of water (1000 kg/m³).
(c) Upthrust while floating: 132.3 N

Question 7. 

A piece of brass weighs 175 gf in air and 150 gf when fully submerged in water. The density of water is 1.0 g cm-3.

(i) What is the volume of the brass piece? (ii) Why does the brass piece weigh less in water? 

Ans:

(i) Finding the Volume of the Brass Piece

We are told the piece of brass weighs 175 gf in air and 150 gf when submerged in water.

The apparent loss of weight when submerged is a result of the upward buoyant force acting on the object. The magnitude of this buoyant force is exactly equal to the weight of the fluid displaced by the object.

• Weight loss in water: 175 gf – 150 gf = 25 gf.

This means the buoyant force acting on the brass is 25 gf. By Archimedes’ principle, this force equals the weight of the water displaced. Therefore, the weight of the water displaced is also 25 gf.

We are given the density of water as 1.0 g cm⁻³. Density is mass per unit volume, and since the gram-force (gf) is the weight of a 1-gram mass, we can work with mass directly.

• Mass of water displaced: 25 grams.
• Density of water: 1.0 g/cm³.

We can now find the volume of this displaced water using the formula:

Volume = Mass / Density

• Volume of displaced water = 25 g / 1.0 g/cm³ = 25 cm³.

When the brass is fully submerged, it displaces a volume of water equal to its own volume.

Therefore, the volume of the brass piece is 25 cm³.

(ii) Why the Brass Piece Weighs Less in Water

The brass piece weighs less in water because of the upward force, known as buoyancy, exerted by the water.

When the brass is immersed, it displaces a certain volume of water. The surrounding water pushes back against the object from all sides, but the pressure is greater on the bottom surface of the object than on the top due to the increasing depth of the water. 

This upward buoyant force acts in the opposite direction to the downward force of gravity (the object’s weight). The scale reading shows the net force. So, when the scale reads 150 gf in water, it is measuring the object’s true weight (175 gf) minus the upward buoyant force (25 gf), making it seem lighter.

Question 8.

A metal cube of edge 5 cm and density 9 g cm-3 is suspended by a thread so as to be completely immersed in a liquid of density 1.2 g cm-3. Find the tension in thread. (Take g = 10 m s-2) 

Ans:

A Walk-Through of the Floating Cube Problem

Let’s break down this physics problem about a cube suspended in a liquid. We’ll be meticulous with units, converting everything into the standard SI system (meters, kilograms, seconds) right from the start to keep things clean and avoid errors.

Question 9. 

A block of wood is floating on water with its dimensions 50 cm x 50 cm x 50 cm inside water. Calculate the buoyant force acting on the block. Take g = 9.8 N kg-1.

Ans:

A buoyant force pushes up on an object submerged in a fluid. For a floating object, this force perfectly balances the object’s weight. We can calculate it using Archimedes’ principle, which states that the buoyant force is equal to the weight of the fluid displaced by the object.

Step 1: Find the Volume of the Displaced Water

The block is floating, but the problem states its dimensions are “50 cm x 50 cm x 50 cm inside water.” This means the entire volume of the block is submerged beneath the water’s surface.

First, let’s calculate this volume in cubic meters (m³), as the standard unit for density is kg/m³.

• Side of the block = 50 cm = 50 / 100 = 0.5 m
• Volume of block, V = side × side × side = 0.5 m × 0.5 m × 0.5 m = 0.125 m³

Since the entire block is submerged, the volume of water displaced, V_displaced, is equal to the volume of the block.
V_displaced = 0.125 m³

Step 2: Find the Mass of the Displaced Water

We know the density of water, ρ_water, is 1000 kg/m³.
Mass is calculated as density multiplied by volume.

• Mass of displaced water, m = ρ_water × V_displaced
• m = 1000 kg/m³ × 0.125 m³
• m = 125 kg

Step 3: Calculate the Weight of the Displaced Water

The weight of an object is given by its mass multiplied by the acceleration due to gravity (g).

• Weight, W = m × g
• W = 125 kg × 9.8 N/kg
• W = 1225 N

Step 4: Apply Archimedes’ Principle

According to Archimedes’ principle, the buoyant force acting on the block is numerically equal to the weight of the water it displaces.

Final Answer:

The buoyant force acting on the wooden block is 1225 Newtons (N).

Question 10. 

A body of mass 3.5 kg displaces 1000 cm3 of water when fully immersed inside it. Calculate: the volume of the body, the upthrust on the body and the apparent weight of the body in water.

Ans:

Exercise 5 (B)

Question 1. 

Define the term density.

Ans:

A material’s density reveals how tightly its matter is concentrated. It answers a simple but important question: for a given amount of space, how much “stuff” is actually inside?

Scientifically, this is calculated as the amount of mass contained within a specific unit of volume. The relationship is captured by a straightforward equation:

Density = Mass ÷ Volume

To picture this, consider two identical suitcases.

One is meticulously packed with clothes, rolled tightly to fit as much as possible. This suitcase is heavy for its size, demonstrating a high density. The materials inside are packed closely together.

The other suitcase is filled only with a few fluffy pillows. It is light and easy to carry, showing a low density. The same volume is occupied by far less material, with its matter being much more spread out.

This concept of relative density, or how dense one material is compared to another, governs why objects float or sink. A massive wooden ship floats because the wood and the air-filled spaces within its hull create an overall structure that is less dense than the body of water it rests on. Conversely, a solid steel nail, though small, sinks immediately because its material is far denser than water. At its heart, density measures how much mass is squeezed into a defined space.

Question 2. 

What is the unit density in (i) C.G.S. and (ii) S.I. systems?

Ans:

What is Unit Density?

Density is a measure of mass per unit volume. In simpler terms, it tells us how much “stuff” is packed into a given space. 

(i) Unit Density in the C.G.S. System

The C.G.S. system stands for Centimeter-Gram-Second.

• Mass is measured in grams (g).
• Length is measured in centimeters (cm). Therefore, volume (length × width × height) is measured in cubic centimeters (cm³).

Following the formula for density (ρ = mass / volume), the unit of density in the C.G.S. system is:

Gram per cubic centimeter (g/cm³).

Practical Significance:
This unit is very intuitive for small-scale objects and laboratory work. For example, the density of pure water at 4°C is almost exactly 1 g/cm³. This makes it easy to visualize and compare the densities of other materials directly against water.

(ii) Unit Density in the S.I. System

The S.I. system (Système International d’Unités) is the modern form of the metric system and is used globally in science and engineering.

• Mass is measured in kilograms (kg).
• Length is measured in meters (m). Therefore, volume is measured in cubic meters (m³).

Therefore, the unit of density in the S.I. system is:

Kilogram per cubic meter (kg/m³).

Practical Significance:
While scientifically precise, the kg/m³ unit is less intuitive for everyday objects because a cubic meter is a very large volume. For instance, the density of water is 1000 kg/m³. This unit is most useful in engineering, fluid dynamics, and large-scale calculations.

Question 3. 

Express the relationship between the C.G.S. and S.I. units of density. 

Ans:

Understanding the Link Between Density Units

Density provides a measure of how much mass is packed into a given space, calculated by dividing an object’s mass by its volume. The connection between its units in different measurement systems arises directly from how those systems define their fundamental quantities.

The Gram per Cubic Centimeter (C.G.S. Unit)

In the Centimeter-Gram-Second (C.G.S.) system, which builds upon the centimeter, gram, and second, the logical unit for density is the gram per cubic centimeter (g/cm³). This is a naturally convenient unit; for instance, the density of pure water is approximately 1 g/cm³.

The Kilogram per Cubic Meter (S.I. Unit)

The International System of Units (S.I.) uses the meter, kilogram, and second as its base. Consequently, the standard unit for density becomes the kilogram per cubic meter (kg/m³). At first glance, these two units, g/cm³ and kg/m³, appear quite different.

Connecting the Two Through Conversion

The bridge between these units is built by converting both the mass and the length components.

1. Mass Conversion: The first link is straightforward. One kilogram is defined as one thousand grams.
   • 1 kg = 1000 g
2. Volume Conversion: This is the crucial step. A cubic meter is not merely 100 cubic centimeters. Since volume is length cubed, we must cube the conversion factor for length.
   • 1 m = 100 cm
   • 1 m³ = (100 cm)³ = 100 cm × 100 cm × 100 cm = 1,000,000 cm³ (or 10⁶ cm³)

Now, we can express one S.I. density unit in terms of the C.G.S. unit:

1 kg/m³ = 1 kg / 1 m³

Substituting the conversions we just established: = 1000 g / 1,000,000 cm³

Simplifying this fraction: = 1000 / 1,000,000 g/cm³ = 1 / 1000 g/cm³ = 0.001 g/cm³

The Practical Relationship

From the above, we see that 1 kg/m³ is equal to 0.001 g/cm³. For practical use, it is often more useful to state the inverse relationship:

1 g/cm³ = 1000 kg/m³

This means a density expressed in grams per cubic centimeter is numerically one thousand times larger than the same density expressed in kilograms per cubic meter. For example, the density of aluminum is about 2.7 g/cm³, which is equivalent to 2,700 kg/m³.

In summary, the factor of 1000 connecting these units is a direct and inevitable result of the definitions within the metric system: a kilogram is 10³ times a gram, and a cubic meter is 10⁶ times a cubic centimeter, leading to a net conversion factor of 10³ / 10⁶ = 10⁻³, or its reciprocal, 10³.

Question 4.

‘The density of iron is 7800 kg m-3’. What do you understand by this statement?

Ans:

When we say “The density of iron is 7800 kg m⁻³,” it is a precise way of describing how much ‘stuff’—or mass—is packed into a given amount of space.

Here’s a breakdown of what that means:

1. It’s a Measure of ‘Heaviness for Size’: Imagine you have two identical cubes, one made of iron and one made of wood. The iron cube would feel much heavier. This is because iron has a higher density; more of its matter is squeezed into the same volume.
2. Decoding the Units (kg m⁻³): This is read as “kilograms per cubic meter.”
   • A cubic meter (m³) is the standard unit for volume. It’s a fairly large space, equivalent to a cube where each side is one meter long (like a large washing machine or a small kennel).
   • A kilogram (kg) is the standard unit for mass (similar to weight for our everyday purposes).
3. Putting It All Together: The statement tells us that if you were to take a perfectly solid block of iron measuring exactly one cubic meter, it would have a mass of 7800 kilograms.

To put that number into perspective, a cubic meter of water has a mass of about 1000 kg. So, iron is roughly 7.8 times “heavier” or more massive than an equal volume of water. This high density is a fundamental property of iron and metals like it, which is why they feel so solid and are used in construction where strength and weight are important. It’s a fixed value that helps engineers and scientists calculate the mass of an iron object just by knowing its volume, and vice-versa.

Question 5. 

Write the density of water at 4°C in S.I. unit .

Ans:

We often think of substances becoming steadily denser as they cool, but water has a fascinating and life-preserving quirk. While it does contract and become denser as it cools from room temperature, this trend reverses just before it freezes. The point of greatest compaction for a sample of pure water isn’t in its solid form, but at a specific point in its liquid life: 4 degrees Celsius.

In the International System of Units (S.I.), which uses the kilogram and the cubic meter as its base units for mass and volume, this peak density is quantified as 1000 kilograms per cubic meter (kg/m³).

This value is far from arbitrary; it is deeply embedded in the history of measurement. The original definition of the kilogram at the end of the 18th century was directly tied to this physical property. It was established as the mass of one cubic decimeter of pure water at its point of maximum density. Although the modern kilogram is now defined by a fundamental physical constant, this historical link explains the perfect, round-number relationship: one liter (a cubic decimeter) of water at 4 °C has a mass of exactly one kilogram. This elegant connection between the metric unit of volume and the unit of mass was intentionally engineered by its creators.

Question 6. 

How are the (i) Mass, (ii) Volume and (iii) Density of a metallic piece affected, if at all, with an increase in temperature?

Ans:

When a metallic piece, like a steel bolt or a copper coin, is heated up, its fundamental properties change in the following ways:

(i) Mass: Unchanged

The mass of the metallic piece remains completely unaffected by the increase in temperature. Mass is a measure of the actual amount of matter, the total number of atoms, present in the object. Heating the metal does not create or destroy these atoms; it only changes how much they move and the space between them. So, whether the metal is freezing cold or glowing hot, its mass stays constant.

(ii) Volume: Increases

This is the most noticeable change. As the temperature rises, the atoms within the metal gain kinetic energy and vibrate more intensely. These stronger vibrations push the atoms slightly farther apart from each other. Because this happens in all three dimensions (length, width, and height), the entire piece of metal expands. This phenomenon is known as thermal expansion. You can observe this in everyday life, such as with gaps left between railway tracks to accommodate this expansion on a hot day.

(iii) Density: Decreases

Density is defined as mass per unit volume (Density = Mass / Volume). Since we’ve established that the mass stays the same while the volume increases, the result is a straightforward mathematical decrease in density. The same amount of mass is now spread out over a larger volume, making the metal less dense when it is hot. This is why hot air rises, and the same principle applies to liquids and solids—a heated metal becomes slightly less dense than its cooler surroundings.

Question 7. 

Water is heated from 0°C to 10°C . How does the density of water change with temperature?

Ans:

Water exhibits a unique and counterintuitive behavior in its density change between 0°C and 10°C. Unlike most substances, which become steadily denser as they cool, water does not follow a linear path.

The density of water initially increases as it warms from 0°C to 4°C, and then decreases from 4°C to 10°C and beyond.

Here is a breakdown of this phenomenon:

1. From 0°C to 4°C: The Increase in Density

At 0°C, in its solid state as ice, water molecules are locked into a rigid, hexagonal crystal lattice. This structure holds the molecules further apart on average than in the liquid state, which is why ice is less dense and floats.

When ice melts to become liquid water at 0°C, this crystalline structure collapses. However, numerous fragments of this open, hydrogen-bonded network still persist temporarily. As the water is warmed from 0°C to 4°C, the primary effect is not the typical thermal expansion (which would decrease density), but the continued breakdown of these residual, low-density ice-like structures.

The collapse of these open cages allows the molecules to pack more closely together. This increase in molecular packing efficiency outweighs the slight expansion caused by the increased molecular vibration from the heat. Consequently, the volume of a given mass of water decreases, and its density increases, reaching a maximum at 4°C.

2. At 4°C: The Point of Maximum Density

At this precise temperature, the balance tips. The disruptive effect of the broken hydrogen-bond networks is maximized, and the water molecules are arranged in the most compact way possible for liquid water. No other temperature yields a higher density for liquid water under standard conditions.

3. From 4°C to 10°C: The Decrease in Density

Beyond 4°C, the “normal” behavior of liquids takes over. The thermal energy supplied to the water now primarily increases the kinetic energy of the molecules. They vibrate more vigorously and push against their neighboring molecules, requiring more space. This phenomenon, known as thermal expansion, becomes the dominant factor.

As the volume increases with a constant mass, the density begins to decrease steadily as the temperature rises from 4°C to 10°C and continues to do so as it is heated further.

In summary, the relationship is not one-directional. The density of water first increases, peaks at 4°C, and then decreases as it is heated from 0°C to 10°C. This unique property, caused by the interplay between molecular packing and hydrogen bonding, is crucial for the survival of aquatic life, as it causes the densest 4°C water to sink to the bottom of lakes in winter, preventing them from freezing solid.

Question 8. 

1. Complete the following sentence. Mass = ……………….. × density 

2. Complete the following sentence. S.I. unit of density is ………. . 

3. Complete the following sentence. The density of water is …. … kg m-3. 

4. Complete the following sentence. Density in kg m-3 =  ………… × density in g cm-3

Ans:

1. Complete the following sentence. Mass = Volume × density
2. Complete the following sentence. S.I. unit of density is kilogram per cubic metre (kg/m³).
3. Complete the following sentence. The density of water is 1000 kg m⁻³.
4. Complete the following sentence. Density in kg m⁻³ = 1000 × density in g cm⁻³

Question 9. 

What do you understand by the term relative density of a substance?

Ans:

Understanding Relative Density: A Measure of Heaviness

At its core, relative density is a straightforward concept that answers a simple question: for the same amount of space, how much heavier is one material compared to another? It’s a comparison of “heft,” stripping away complex units to give a clean, comparable number.

The universal yardstick for this measurement, for nearly all solids and liquids, is pure water at 4° Celsius—the temperature at which it reaches its maximum density. This makes the concept incredibly practical, as it directly relates a material’s behavior to our most common liquid.

The Mathematical Relationship

The definition is clean and unitless:

Relative Density = (Density of a Substance) / (Density of Reference Substance, usually water)

Because you are dividing a density by another density (e.g., g/cm³ by g/cm³), the units cancel out. The result is a pure number, a simple multiplier that tells you how the substance stacks up against water.

Interpreting the Value

The number you get isn’t just abstract; it has immediate physical meaning:

• A Value of 1: The substance is a density match for water. An object made from it will neither sink nor float readily, but will hover suspended in the water column.
• A Value Greater than 1: This indicates a material that is denser than water. Such an object will sink. For example, a relative density of 7.8 means the substance is 7.8 times denser than an equal volume of water. A solid piece of it will always sink.
• A Value Less than 1: This signals a material that is lighter than water. An object made from it is buoyant and will float. A value of 0.85, for instance, means the substance is only 85% as dense as water, so 85% of it will be submerged while it floats.

Practical Applications in Everyday and Professional Life

This concept is more than a textbook idea; it’s a useful tool in many contexts:

• Predicting Floating and Sinking: The most immediate application is knowing if something will float. From designing boats and buoys to understanding why a heavy log of wood floats while a small metal key sinks, relative density provides the instant answer.
• Assessing Purity and Composition: Pure substances have a specific, known relative density. If you measure the relative density of a sample of gold and it’s lower than the standard value, it’s a clear sign that the gold is alloyed with a less dense metal. This principle is used to test the quality of fuels, oils, and other liquids.
• A Tool for Simplicity and Comparison: It is far simpler to recall that the relative density of lead is 11.3 than to remember its precise density is 11,340 kg/m³. This simplification makes mental calculations and comparisons between different materials much faster and more intuitive.

Question 10. 

What is the unit of relative density?

Ans:

The unit of relative density is no unit at all.

It is a dimensionless quantity.

Here’s the simple reason why: Relative density is a ratio. It is calculated by dividing the density of a substance by the density of a standard reference substance (which is water for liquids and solids).

Because you are dividing a density (e.g., kg/m³) by another density (also kg/m³), the units cancel each other out completely.

In simple terms:
Imagine you have a piece of iron. You find that the density of iron is 7800 kg/m³. The density of water is 1000 kg/m³.

The relative density is calculated as:
(7800 kg/m³) / (1000 kg/m³) = 7.8

The “kg/m³” units cancel, leaving you with just the pure number 7.8. This number tells you that iron is 7.8 times denser than water. It’s a straightforward comparison, so it doesn’t need a unit.

Question 11. 

Differentiate between density and relative density of a substance. 

Ans:

Feature	Density (ρ)	Relative Density (RD or SG)
Definition	It is an absolute measure of a substance’s mass contained per unit volume.	It is a dimensionless ratio comparing a substance’s density to the density of a standard reference substance.
Formula	Ρ = Volume / Mass​= V / m​	RD = Density of Reference Substance / Density of Substance​
Units	Has units (e.g., kg/m3 or g/cm3).	It is unitless (dimensionless) because it is a ratio of two quantities with the same units.
Measurement	Measures the intrinsic property of the substance itself.	Measures how dense a substance is compared to another, usually water (for liquids/solids) or air (for gases).
Reference	No reference substance is needed.	Requires a reference substance (e.g., water at 4∘C).

Question 12. 

With the use of Archimedes’ principle, state how you will find relative density of a solid denser than water and insoluble in it. How will you modify your experiments if the solid is soluble in water? .

Ans:

Part 1: Finding Relative Density of an Insoluble Solid (e.g., Metal)

Aim: To find the relative density of a solid denser than and insoluble in water.

Principle: Archimedes’ Principle. The buoyant force equals the weight of the fluid displaced.

Procedure:

1. Suspend the solid from a spring balance and note its weight in air. Let this be W₁.
2. Immerse the solid completely in water without touching the beaker. Note the new weight. Let this be W₂.

Calculation:

• Loss of weight in water (Buoyant force) = W₁ – W₂
• This loss equals the weight of water displaced by the solid.
• Relative Density (R.D.) = W₁ / (W₁ – W₂)

Part 2: Finding Relative Density of a Water-Soluble Solid (e.g., Salt, Sugar)

Aim: To find the relative density of a solid that dissolves in water.

Modification: Use a liquid in which the solid does not dissolve, like kerosene.

Procedure:
This is a two-step method.

Step 1: Find the Relative Density of Kerosene

1. Weigh a dense, insoluble solid (sinker) in air. Weight = A.
2. Weigh it completely immersed in water. Weight = B.
3. Weigh it completely immersed in kerosene. Weight = C.
4. R.D. of Kerosene = (A – C) / (A – B)

Step 2: Find the Relative Density of the Soluble Solid

1. Weigh the soluble solid in air. Weight = W_air.
2. Weigh it completely immersed in kerosene. Weight = W_kerosene.

Calculation:

• Relative Density of Solid = (W_air × R.D._kerosene) / (W_air – W_kerosene)

Question 13. 

A body weighs W gf in air and W1 gf when it is completely immersed in water. Find: (i) Volume of the body, (ii) Upthrust on the body and (iii) Relative density of the material of the body. 

Ans:

Question 14. 

Describe an experiment, using Archimedes principle, to find relative density of a liquid. 

Ans:

Experiment: Finding a Liquid’s Relative Density Using a Solid

Aim: Use a solid that sinks in liquids to find the relative density (specific gravity) of a test liquid like saltwater or oil by applying Archimedes’ principle.

Principle: Archimedes’ principle says a submerged object is pushed upward by a force equal to the weight of the fluid it displaces. For a fully submerged solid, the weight loss in a fluid equals the weight of the displaced fluid. By comparing this weight loss in the test liquid to that in pure water, we find the liquid’s relative density.

Formula:
Relative Density of Liquid = (Weight loss in liquid) / (Weight loss in water)

Materials:

• A solid sinking in both water and test liquid (e.g., metal piece, stone)
• Test liquid (e.g., saltwater, oil)
• Pure water in a beaker
• Spring balance
• Thin thread
• Stand with clamp

Procedure:

1. Weight in Air: Hang the solid from the spring balance using thread. Note its weight in air as Wₐᵢᵣ.
2. Weight in Water: Place the beaker of water below the object. Submerge the object fully without letting it touch the container. Record the new weight as W_water. Calculate the loss in water:
   Loss_water = Wₐᵢᵣ – W_water.
3. Weight in Test Liquid: Dry the object. Replace the water beaker with the test liquid. Fully submerge the object again and note the weight as W_liquid. Calculate the loss in liquid:
   Loss_liquid = Wₐᵢᵣ – W_liquid.
4. Calculation: Compute the relative density:
   R.D. = Loss_liquid / Loss_water.

Why It Works: The object displaces the same volume of fluid each time. The weight loss ratio directly gives the density ratio of the liquids because the buoyant force depends on the density of the displaced fluid.

Tips for Accuracy:

• Use the same solid for all measurements.
• Ensure the object is fully submerged and still for readings.
• Remove any air bubbles stuck to the object.
• Dry the object between liquids to prevent mixing.

Question 15. 

A body weighs W1gf in air and when immersed in a liquid it weighs W2gf, while it weighs W3gf on immersing it in water. Find: (i) volume of the body (ii) upthrust due to liquid (iii) relative density of the solid and (iv) relative density of the liquid.

Ans:

To analyze an object using buoyancy, we begin with its measured weights: one in open air, another while submerged in a specific liquid, and a final one while fully immersed in water. The core principle at work is that a submerged object is pushed upward by a force equal to the weight of the fluid it displaces.

Calculating the Object’s Volume
When the object is placed in water, its apparent weight decreases. This loss of weight is not a change in the object itself, but rather the effect of the water pushing back against it with a force equal to the weight of the displaced water. Since we know the density of water is 1 gram per cubic centimeter, the mass of this displaced water (in grams) gives us the object’s volume directly in cubic centimeters. We find this by simply subtracting the object’s weight in water from its weight in air.

Measuring the Liquid’s Upward Push (Buoyant Force)
The liquid also exerts an upward push on the object. The strength of this push is revealed by how much lighter the object seems when immersed in the liquid. We calculate this buoyant force by finding the difference between the object’s weight in air and its weight while submerged in that particular liquid.

Finding the Solid Material’s Specific Gravity
We can determine how dense the object’s material is compared to water, a property known as its specific gravity or relative density. This is done by comparing the object’s actual weight to the weight of the water it displaces. In practice, this is a simple ratio: the weight in air divided by the reduction in weight observed when it is submerged in water.

Finding the Liquid’s Specific Gravity
Similarly, we can find out how dense the liquid is relative to water. This is done by comparing the liquid’s buoyant effect to that of water. Essentially, we take the ratio of the object’s weight loss in the liquid to its weight loss in water. This tells us the liquid’s relative density.

Exercise 5 (B)

Question 1. 

Relative density of a substance is expressed by comparing the density of that substance with the density of : 

1. Air
2. Mercury 
3. Water
4. Iron

Question 2. 

The unit of relative density is : 

1. g cm-3 
2. kg m-3 
3. m3 kg-1
4. no unit

Question 3. 

The density of water is : 

1. 1000 g cm-3
2. 1 kg m-3
3. 1 g cm-3
4. None of these.

Exercise 5 (B)

Question 1. 

The density of copper is 8.83 g cm-3. Express it in kg m-3. 

Ans:

Converting Copper’s Density from g/cm³ to kg/m³

When working across different scientific fields, it’s often necessary to convert units. Let’s transform the density of copper, 8.83 grams per cubic centimeter (g/cm³), into the standard SI unit of kilograms per cubic meter (kg/m³). This process is essentially one large multiplication by the number “1,” cleverly disguised using conversion factors.

The most efficient way to perform this conversion is to recognize the direct relationship between the units. We are converting both the mass (g → kg) and the volume (cm³ → m³) simultaneously.

Question 2. 

The relative density of mercury is 13.6. State its density in

(i) C.G.S. unit and

(ii) S.I. unit. 

Ans:

The relative density, which is a simple measure of how heavy a substance is compared to water, tells us that mercury is 13.6 times heavier than an equal volume of water. To find its actual density, we just need to perform a straightforward calculation using the density of water for each unit system.

(i) Density in the C.G.S. unit:

In the C.G.S. system, we measure density in grams per cubic centimeter (g/cm³). Since the density of water is exactly 1 g/cm³, the calculation is very simple.

The density of mercury is:
= 13.6 × 1 g/cm³
= 13.6 g/cm³

(ii) Density in the S.I. unit:

In the S.I. system, density is measured in kilograms per cubic meter (kg/m³). Here, the density of water is 1000 kg/m³.

Therefore, the density of mercury becomes:
= 13.6 × 1000 kg/m³
= 13,600 kg/m³

To put it simply:

In S.I. terms, it’s 13,600 kg/m³.

In C.G.S. terms, it’s 13.6 g/cm³.

Question 3. 

The density of iron is 7.8 x 103 kg m-3. What is its relative density? 

Ans:

Understanding How Dense Iron Really Is

We often hear that iron is a “heavy” metal, but a much more useful question is: “How much heavier is it than water?” This is exactly what the concept of relative density, sometimes called specific gravity, helps us figure out. It’s not about finding a weight, but about making a direct comparison.

At its heart, relative density is a simple comparison. It’s a number that answers the question: “How many times denser is this material than pure water?” 

The Golden Rule of Relative Density

The formula is beautifully straightforward:

Relative Density = (Density of Your Material) / (Density of Water)

For this to work, the densities for both the material and water absolutely must be in the same units. If they aren’t, it’s like comparing miles to kilometers without converting; the answer will be meaningless.

The Key Player: The Density of Water

To be the universal standard for comparison, we need a fixed density for water. In the metric system, which is designed for this kind of simplicity, the density of water is a wonderfully clean number:

Density of Water = 1000 kg/m³

We can also write this as 1.0 × 10³ kg/m³ to make calculations with scientific notation easier.

Applying the Concept to Iron

Now, let’s look at our subject, iron. We are told that:

Density of Iron = 7.8 × 10³ kg/m³

Notice that both this and the density of water are in the exact same units (kg/m³). This means we can plug them directly into our formula without any messy conversions.

The calculation looks like this:

Relative Density of Iron = (7.8 × 10³ kg/m³) / (1.0 × 10³ kg/m³)

The “Aha!” Moment of Simplification

This is where the elegance of the metric system shines. The units of kg/m³ in the top and bottom cancel each other out completely, leaving us with a pure, unitless number—exactly what we want for a ratio.

Furthermore, the 10³ (which means 1000) on the top and bottom also cancel out.

So, we are left with:

Relative Density of Iron = 7.8 / 1.0 = 7.8

What This Number Truly Means

The result, 7.8, is powerful in its simplicity. It tells us that iron is 7.8 times denser than water. This isn’t just a abstract math result; it has a direct physical consequence.

This is why a solid chunk of iron will immediately sink when placed in water. For an object to float, it must be less dense than the fluid it’s in. Since iron is nearly eight times denser, it has no chance of floating and will always displace a volume of water that weighs much less than itself.

Question 4.

The relative density of silver is 10.8. Find its density.  

Ans:

A substance’s relative density, often called its specific gravity, serves as a practical measure to compare its heaviness to that of water. Since it is a pure ratio, this number carries no units. When we say silver has a relative density of 10.8, it means that a given chunk of silver is 10.8 times more massive than a chunk of water of identical size.

To move from this relative comparison to a concrete density value, we simply combine it with the absolute density of water in the unit system we wish to use.

Calculating the Density in the C.G.S. Framework:

Within the Centimeter-Gram-Second (C.G.S.) system, the standard unit for density is grams per cubic centimeter (g/cm³). A fundamental standard here is that pure water has a density of exactly 1 g/cm³.

Consequently, silver’s density is found through this direct calculation:
= Specific Gravity of Silver × Mass of a Cubic Centimeter of Water
= 10.8 × 1 g/cm³
= 10.8 g/cm³

Calculating the Density in the S.I. Framework:

The International System of Units (S.I.) specifies density in kilograms per cubic meter (kg/m³). In this system, the density of water is fixed at 1000 kg/m³.

Applying the same principle gives us the density of silver as:
= Specific Gravity of Silver × Mass of a Cubic Meter of Water
= 10.8 × 1000 kg/m³
= 10,800 kg/m³

Final Results:

• Expressed in C.G.S. units, the density of silver is 10.8 g/cm³.
• Expressed in S.I. units, the density of silver is 10,800 kg/m³.

Question 5. 

Calculate the mass of a body whose volume is 2 m3 and relative density is 0.52. 

Ans:

Finding an Object’s Mass Using Its Relative Density

When we need to determine the mass of an object but don’t have a scale, we can use its physical properties as a workaround. If we know how much space it occupies (its volume) and its relative density, the calculation becomes straightforward. Let’s work through an example where a body has a volume of 2 cubic meters and a relative density of 0.52.

Part 1: Decoding What Relative Density Means

Relative density, often called specific gravity, is a useful number that compares a material’s density to a well-known standard: the density of water. Think of it as a measure of how “heavy” a material is for its size compared to water.

Question 6. 

Calculate the mass of air in a room of dimensions 4.5 m × 3.5 m × 2.5 m if the density of air at N.T.P. is 1.3 kgm-3 . 

Ans:

To find the mass of the air inside the room, we need to perform two main steps. First, we must determine the volume of space the room encloses. Then, we use the given density to calculate the mass of the air filling that volume.

Step 1: Calculate the Volume of the Room

The room is a rectangular cuboid, so its volume is found by multiplying its length, width, and height.

• Length = 4.5 m
• Width = 3.5 m
• Height = 2.5 m

Volume (V) = Length × Width × Height
V = 4.5 m × 3.5 m × 2.5 m
V = 39.375 m³

Step 2: Calculate the Mass of the Air

We know the density (ρ) of air is 1.3 kg for every cubic meter (kg/m³). 

Mass (M) = Density × Volume
M = ρ × V
M = 1.3 kg/m³ × 39.375 m³
M = 51.1875 kg

For a final answer, we can round this to a sensible number of significant figures. The dimensions of the room are given to two significant figures (4.5, 3.5, 2.5), and the density is given to two (1.3).

Therefore, the mass of the air is approximately 51 kg.

Final Answer:
The mass of the air in the room is 51 kg.

Question 7. 

A piece of stone of mass 113 g sinks to the bottom in water contained in a measuring cylinder and water level in the cylinder rises from 30 ml to 40 ml. Calculate R.D. of stone.

Ans:

Determining the Relative Density of a Stone

A fundamental concept in material science is relative density, also known as specific gravity. It provides a dimensionless measure of how dense a substance is compared to a reference, which for solids and liquids is typically pure water. This value tells us if an object will sink or float and can help identify the material it’s made of.

The principle is straightforward: relative density (R.D.) is the ratio of the density of a substance to the density of water. Since the density of water is conveniently 1 gram per cubic centimeter (g/cm³), this calculation simplifies immensely. In practice, it means the R.D. is numerically equal to the ratio of the mass of the object to the mass of the water it displaces.

Step-by-Step Analysis with the Stone

Let’s apply this principle to the given data for the stone.

1. Determine the Stone’s Mass:
   The mass is directly provided by the measurement on a scale. We know the stone has a mass of 113 grams.
2. Determine the Stone’s Volume (using water displacement):
   The volume is found by observing how much the water level rises when the stone is submerged.
   • Initial water level in the graduated cylinder: 30 ml
   • Final water level after adding the stone: 40 ml
   • Therefore, the volume of the stone is 40 ml – 30 ml = 10 ml.
3. A key point of conversion is that 1 milliliter (ml) is exactly equal to 1 cubic centimeter (cm³). So, the stone’s volume is 10 cm³.
4. Calculate the Mass of the Displaced Water:
   Since the stone has a volume of 10 cm³, it must displace an equal volume of water. Using the density of water (1 g/cm³), we can find the mass of this displaced water.
   • Mass of displaced water = 10 cm³ × 1 g/cm³ = 10 grams.
5. Calculate the Relative Density:
   Following the definition, we divide the mass of the stone by the mass of the water it displaces.
   • R.D. = Mass of Stone / Mass of Displaced Water
   • R.D. = 113 g / 10 g = 11.3

Question 8. 

A body of volume 100 cm3 weighs 1 kgf in air. Find: Its weight in water and Its relative density.

Ans:

Imagine holding an object that weighs exactly 1 kilogram-force on a scale in the air. Now, you lower it into a tank of water. You’ll notice the scale reading drops because the water pushes up on the object with a force. This push, known as the buoyant force, is exactly equal to the weight of the water your object has taken the place of.

Since your object has a size of 100 cubic centimeters, it forces 100 cubic centimeters of water aside. We know that a single cubic centimeter of water weighs about 1 gram-force. So, the 100 cm³ of displaced water has a total weight of 100 gram-force, which is the same as 0.1 kilogram-force. This 0.1 kgf is the strength of the water’s upward push.

To find what the scale shows underwater, you take the object’s real weight and subtract this helpful upward push from the water.

Scale Reading in Water = Weight in Air – Buoyant Force
= 1.0 kgf – 0.1 kgf
= 0.9 kgf

Now, to find out how dense the object’s material is compared to water, we can use a neat trick. You compare its actual weight to the weight it seems to lose when submerged. The object felt 0.1 kgf lighter in the water.

So, its relative density is a simple division:
Relative Density = (Weight in Air) / (Weight Loss in Water)
= 1.0 kgf / 0.1 kgf
= 10

This tells us the object’s material is ten times denser than water.

Final Answers:

• The object’s apparent weight in water is 0.9 kgf.
• The object has a relative density of 10.

Question 9. 

A body of mass 70 kg, when completely immersed in water, displaces 20,000 cm3 of water. Find: (i) The weight of the body in water and (ii) The relative density of material of the body. 

Ans:

Determining Weight in Water and Relative Density

Imagine you’re trying to figure out how a heavy object behaves when submerged in water. You know its mass is 70 kg, and when you immerse it completely, it pushes aside 20,000 cm³ of water. Our goal is to find two things: what the object seems to weigh while underwater, and the relative density (or specific gravity) of the material it’s made from.

Let’s break this down step-by-step.

Step 1: Getting Our Units in Order

First, we notice a unit mismatch. The body’s mass is in kilograms (kg), but the displaced water volume is in cubic centimeters (cm³). Since the density of water is given as 1000 kg/m³, it’s best to work in cubic meters (m³) for consistency.

We know:
1 m³ = 1,000,000 cm³

Therefore, to convert the displaced volume:
20,000 cm³ ÷ 1,000,000 = 0.02 m³

So, the body displaces 0.02 cubic meters of water.

Step 2: Finding the Upthrust (Buoyant Force)

Archimedes’ principle tells us that the upward force (upthrust) on a submerged object is equal to the weight of the fluid it displaces.

First, let’s find the mass of that displaced water:
Mass of water = Density × Volume = 1000 kg/m³ × 0.02 m³ = 20 kg.

In the context of weight (using kilogram-weight, kg-wt, where 1 kg mass has a weight of 1 kg-wt), the weight of the displaced water is 20 kg-wt. This weight of the displaced fluid is precisely the buoyant force pushing upwards on the object.

Step 3: Calculating the Apparent Weight in Water

The object’s actual weight in air is 70 kg-wt. When submerged, the buoyant force supports some of this weight, making it feel lighter.

Weight in Water = Weight in Air − Buoyant Force
Weight in Water = 70 kg-wt − 20 kg-wt = 50 kg-wt

This means a scale would read 50 kg if the object were weighed while underwater.

Step 4: Uncovering the Relative Density

Relative Density (R.D.) is a dimensionless number that tells us how dense a material is compared to pure water. We can find this in two different ways, both leading to the same answer.

Method A: Using Densities Directly

• Density of the Body = Mass / Volume = 70 kg / 0.02 m³ = 3500 kg/m³
• Density of Water = 1000 kg/m³
• Relative Density = Density of Body / Density of Water = 3500 / 1000 = 3.5

Method B: Using Weights (The Elegant Shortcut)
There’s a handy principle in physics: the relative density of a solid is equal to its weight in air divided by its loss of weight in water.

• Weight in Air = 70 kg-wt
• Loss of Weight in Water = Buoyant Force = 20 kg-wt
• Relative Density = 70 kg-wt / 20 kg-wt = 3.5

Both methods confirm our result.

Final Answers:

• The weight of the body in water is 50 kg-wt.
• The relative density of the material is 3.5.

Question 10. 

A solid weighs 120 gf in air and 105 gf when it is completely immersed in water. Calculate the relative density of solid. 

Ans:

When an object is submerged in a fluid, it seems to become lighter due to an upward push from the fluid, known as the buoyant force. The amount of weight it loses is exactly equal to the weight of the fluid it pushes aside.

In this case, the solid seems to lose weight when placed in water.

Its measured weight in air is 120 gf.
Its measured weight while fully underwater is 105 gf.

The weight it seems to lose is its apparent loss in weight, which is also the strength of the buoyant force acting on it.
Buoyant Force = Weight in air – Weight in water
= 120 gf – 105 gf
= 15 gf

According to Archimedes’ principle, this 15 gf buoyant force means the solid displaced an amount of water that itself weighs 15 gf.

The relative density (also called specific gravity) is found by comparing the object’s density to that of water. A simpler way to calculate it without dealing with volume directly is to use the weight values we have.

The relative density of the solid is given by the ratio:

Relative Density = (Weight of Solid in Air) / (Loss of Weight in Water)

Plugging in our values:

Relative Density = 120 gf / 15 gf
= 8

Question 11. 

A solid weighs 32 gf in air and 28.8 gf in water. Find: (i) The volume of solid, (ii) R.D. of solid and (iii) The weight of solid in a liquid of density 0.9 g cm-3. 

Ans:

This problem explores the principles of buoyancy and density using a solid object weighed under different conditions. The given data is:

• Weight of solid in air = 32 gf
• Weight of solid in water = 28.8 gf
• Density of water = 1 g/cm³
• Density of liquid = 0.9 g/cm³

(i) Finding the Volume of the Solid

The key principle here, established by Archimedes, is that when an object is fully submerged in a fluid, it experiences an upward force (buoyancy) equal to the weight of the fluid it displaces. This force is directly responsible for the apparent loss of weight.

(iii) Finding the Weight of the Solid in the Liquid

We now immerse the same solid in a different liquid with a density of 0.9 g/cm³. The principle remains the same: the apparent weight loss will be equal to the weight of the liquid displaced.

1. Calculate the buoyant force (upthrust) in this liquid:
   The buoyant force is determined by the volume of the object and the density of the new liquid.
   • Volume of liquid displaced = Volume of solid = 3.2 cm³
   • Density of liquid = 0.9 g/cm³
   • Mass of liquid displaced = Volume × Density = 3.2 cm³ × 0.9 g/cm³ = 2.88 g
   • Weight of liquid displaced = 2.88 gf (This is the upthrust force).
2. Calculate the apparent weight in the liquid:
   The weight measured in the liquid is the true weight minus the upthrust.
   • Weight in liquid=Weight in air−Upthrust
   • Weight in liquid=32 gf−2.88 gf=29.12 gf

Answer for (iii): The weight of the solid in the liquid is 29.12 gf.

Final Answers Summary

(i) Volume of solid = 3.2 cm³
(ii) Relative density of solid = 10
(iii) Weight of solid in liquid = 29.12 gf

Question 12. 

A body weighs 20 gf in air and 18.0 gf in water. Calculate the relative density of the material of the body. 

Ans:

We can discover how dense a solid object is compared to water by using a simple weighing method. The numbers from the experiment are clear: the object weighs 20 grams-force in the air and seems to weigh only 18 grams-force when completely underwater.

The difference in these two weights is our key to finding the answer. When the object is submerged, it becomes lighter because of the supporting force of the water pushing up against it. This difference is calculated as follows:

20.0 gf (in air) – 18.0 gf (in water) = 2.0 gf

This value of 2.0 gf represents the weight of the volume of water that was pushed aside by the object. In other words, it tells us the weight of an amount of water that takes up the exact same space as the object itself.

A clever trick of physics gives us the relative density. For a solid, we simply compare its actual weight to the weight of the water it displaces. This comparison is made by dividing the weight in air by the weight of the displaced water.

Putting our numbers into this idea gives us:

Relative Density = (Weight of Object) / (Weight of Displaced Water) = 20.0 gf / 2.0 gf

Completing the division gives a final value of 10.

Question 13. 

A solid weighs 1.5 kgf in air and 0.9 kgf in a liquid of density 1.2 × 103 kg m-3. Calculate R. D. of solid.

Ans:

By hanging an object from a spring scale, its weight registers as 1.5 kgf in air. Immersing it completely in a liquid of density 1200 kg/m³ causes the reading to drop to 0.9 kgf. This loss of 0.6 kgf represents the buoyant force.

This upward force equals the weight of the displaced liquid, meaning the mass of the liquid moved is 0.6 kg. Given the liquid’s density, the volume displaced is 0.6 kg / 1200 kg/m³ = 0.0005 m³. This volume is the same as the object’s own volume.

With an object mass of 1.5 kg, its density is 1.5 kg / 0.0005 m³ = 3000 kg/m³. The relative density compared to water is therefore 3000 / 1000 = 3.

Question 14.

A jeweler claims that he makes ornaments of pure gold that have a relative density of 19.3. He sells a bangle weighing 25.25 gf to a person. The clever customer weighs the bangle when immersed in water and finds that it weighs 23.075 gf in water. With the help of suitable calculations, find out whether the ornament is made of pure gold or not.

[Hint : calculate R.D. of material of bangle which comes out to be 11.6].

Ans:

A jeweler states that a certain bangle is crafted from pure gold, which should have a specific gravity of 19.3. To check the truth of this claim, a simple test is conducted using water.

The bangle is first weighed in the open air, showing a value of 25.25 grams-force. It is then weighed again while completely submerged in water, giving a reading of 23.075 grams-force.

The difference between these two weights, known as the loss of weight, is the upward buoyant force exerted by the water. This is calculated as follows:
25.25 grams-force – 23.075 grams-force = 2.175 grams-force.

A fundamental principle used here is that the relative density of a solid object can be found by taking its weight in air and dividing it by the loss of weight it experiences in water.

Applying this formula gives:
Relative Density = 25.25 / 2.175

To simplify the calculation, we can multiply the numerator and denominator by 1000 to eliminate decimals, resulting in 25250 / 2175. Simplifying this fraction, we find it is approximately equal to 1010 / 87. Performing this division gives a final value of roughly 11.6.

The bangle’s measured relative density is approximately 11.6. Since pure gold has a known relative density of 19.3, this result is significantly lower. Therefore, the jeweler’s claim is incorrect, and the ornament is not made of pure gold.

Question 15. 

A piece of iron weighs 44.5 gf in air. If the density of iron is 8.9 × 103, find the weight of the iron piece when immersed in water.

Ans:

To find the iron’s weight in water, we first determine how much space it occupies. Since its density is 8.9 g/cm³ and it weighs 44.5 grams, its volume is 44.5 / 8.9 = 5 cm³.

When submerged, the water pushes upward with a force equal to the weight of the water displaced. Filling the same 5 cm³ volume, water (density 1 g/cm³) has a mass of 5 grams, resulting in an upward force of 5 grams-force.

This buoyant force makes the iron feel lighter. Subtracting this 5 gf push from its original 44.5 gf weight gives an apparent weight of 39.5 gf.

Question 16.

A piece of stone of mass 15.1 g is first immersed in a liquid and it weighs 10.9 gf. Then on immersing the piece of stone in water, it weighs 9.7 gf. Calculate:

The weight of the piece of stone in air, The volume of the piece of stone, The relative density of stone, The relative density of the liquid.

Ans:

Let’s break this problem down using the principle of buoyancy. This force is what causes the apparent loss of weight.

First, we note the given measurements:

• The stone’s weight in air is 15.1 grams-force (gf).
• Its apparent weight when fully submerged in the liquid is 10.9 gf.
• Its apparent weight when fully submerged in water is 9.7 gf.

Finding the Volume of the Stone

The true weight of the stone is 15.1 gf. When it’s in water, its weight drops to 9.7 gf. The difference between these two values is the buoyant force from the water, which is also the weight of the water displaced.

So, the weight of the displaced water = 15.1 gf – 9.7 gf = 5.4 gf.

Since the density of water is 1 gram per cubic centimeter, a weight of 5.4 gf for water means it has a mass of 5.4 grams. Therefore, the volume of that water is 5.4 cm³.

According to Archimedes’ principle, this volume of displaced water is equal to the volume of the stone itself.

• Volume of the stone = 5.4 cm³.

Finding the Relative Density of the Stone

The relative density (or specific gravity) of a solid object can be found by comparing its weight in air to its loss of weight when submerged in water.

The loss of weight in water is the 5.4 gf we just calculated.

Relative Density (stone) = Weight in Air / Loss of Weight in Water
= 15.1 gf / 5.4 gf
= 151/54 ≈ 2.796

Finding the Relative Density of the Liquid

Now, let’s analyze what happens in the liquid. The weight in the liquid is 10.9 gf, so the loss of weight is:

Loss of weight in liquid = 15.1 gf – 10.9 gf = 4.2 gf.

This 4.2 gf represents the weight of the liquid displaced by the stone’s volume.

The relative density of the liquid is the ratio of its density to that of water. A powerful way to find this is to compare the buoyant force it exerts to the buoyant force water exerts for the same object.

Relative Density (liquid) = (Loss of Weight in Liquid) / (Loss of Weight in Water)
= 4.2 gf / 5.4 gf
= 42/54 = 7/9 ≈ 0.778

Final Answers:

• Weight in air: 15.1 gf
• Volume of stone: 5.4 cm³
• Relative Density of stone: 151/54 or approximately 2.796
• Relative Density of liquid: 7/9 or approximately 0.778

Exercise 5 (C)

Question 1. 

State the principle of floatation. 

Ans:

The principle of flotation states that a floating object displaces a volume of fluid whose weight is exactly equal to the object’s own weight.

In simpler terms, for an object to float, it must push aside an amount of water that weighs as much as it does. This is why a heavy steel ship floats—its hollow shape allows it to displace a vast volume of water, and the weight of that displaced water equals the ship’s total weight, providing enough upward push to keep it afloat.

Question 2. 

A body is held immersed in a liquid. (i) Name the two forces acting on the body and draw a diagram to show these forces. (ii) State how the magnitudes of two forces mentioned in part (i) determine whether the body will float or sink in liquid when it is released. (iii) What is the net force on the body if it (a) sinks and (b) floats? 

Ans:

When an object is fully submerged in a fluid, a simple interplay of forces determines its fate.

(i) The Two Forces and a Diagram

The two forces at play are:

1. The Weight of the Body: This is the force due to gravity, pulling the object straight down. It acts through the object’s center of gravity.
2. The Buoyant Force (Upthrust): This is an upward push provided by the liquid. It exists because the pressure at the bottom of the submerged object is greater than the pressure at its top.

A simple diagram would show an object, like a cube, inside a container of liquid. From the center of the object, a downward-pointing arrow is labeled “Weight (W).” From the same center, an upward-pointing arrow of equal or different length is labeled “Buoyant Force (F_b).”

(ii) How the Forces Decide Floating or Sinking

The decision to float or sink rests entirely on the competition between the strength of these two forces the moment the object is released.

• If the buoyant force (F_b) becomes greater than the object’s weight (W), the net upward push wins, and the object will accelerate upwards, eventually rising to float.
• If the object’s weight (W) is greater than the buoyant force (F_b), the downward pull is stronger, and the object will accelerate downwards, meaning it sinks.
• If the two forces are perfectly equal in magnitude, the object will remain suspended wherever it is placed in the liquid, showing no tendency to rise or fall.

(iii) The Net Force in Each Case

The net force is simply the overall force resulting from the combination of the weight and the buoyant force.

(a) When the body sinks: The downward force (weight) is larger. Therefore, the net force acts in the downward direction.
(b) When the body floats: Once it comes to rest at the surface, the upward buoyant force and the downward weight are perfectly balanced. 

Question 3. 

When a piece of wood is suspended from the hook of a spring balance, it reads 70 gf. The wood is now lowered into water. What reading do you expect on the scale of spring balance?

Ans:

When a piece of wood is suspended from a spring balance in air, it reads 70 gf, which represents the weight of the wood. As the wood is lowered into water, it experiences an upward buoyant force due to the water displaced. Since wood is less dense than water (with a typical density less than 1 g/cm³), it will float when immersed. For a floating object, the buoyant force equals the weight of the object. Therefore, the buoyant force acting on the wood is 70 gf, which completely counteracts the weight of the wood. This results in zero net force on the wood, meaning the spring balance does not need to exert any tension to support it. Consequently, the scale of the spring balance will read 0 gf.

This outcome assumes that the wood is allowed to float freely in the water while attached to the spring balance. If the wood were forced to remain fully submerged (which is not typical for wood due to its low density), the reading would be greater than zero but less than 70 gf, depending on the volume and density. However, based on the principle of flotation, the reading is zero.

Question 4. 

A solid iron ball of mass 500 g is dropped in mercury contained in a beaker. (a) Will the ball float or sink? Give reasons. (b) What will be the apparent weight of the ball?

Ans:

(a) Will the ball float or sink?

The ball will float.

Here is the reasoning: Whether an object sinks or floats depends on a simple battle between densities. The ball is made of solid iron, which has a density of about 7.8 g/cm³. Mercury, on the other hand, is an extremely dense liquid with a density of 13.6 g/cm³. Since the iron ball is significantly less dense than the mercury it is placed in, it will not be able to sink. It will be pushed upwards by the buoyant force and will rest on the surface of the mercury, floating partially submerged.

(b) What will be the apparent weight of the ball?

This is because the ball is floating. When an object floats, it is in a state of equilibrium. The upward push from the mercury, known as the buoyant force, perfectly balances the downward pull of gravity on the ball (its true weight). Since these two forces cancel each other out, there is no net force. If you were to try and weigh the ball while it is floating in the mercury, it would not press down on the scale; it would simply register a weight of zero. The mercury is fully supporting it.

Question 5. 

How does the density ρs of a substance determine whether a solid piece of that substance will float or sink in a given liquid ρL? 

Ans:

The Underwater Tug-of-War: Why Some Things Sink and Others Float

Picture yourself at a lake, about to drop a pebble and a stick into the water. You know exactly what will happen: one will plummet to the bottom, while the other will bob on the surface. This everyday phenomenon isn’t a mystery; it’s the clear outcome of a silent contest between two forces. Let’s explore this simple yet powerful principle.

The Two Forces at Play

Imagine an invisible tug-of-war happening the moment an object enters a fluid (like water).

1. The Downward Pull: Gravity. This is the object’s weight, the familiar force pulling it straight down toward the center of the Earth. It’s determined by the object’s mass and the density of the material it’s made from. A solid chunk of iron is heavy for its size because it’s very dense, meaning its atoms are packed tightly together.
2. The Upward Push: The Buoyant Force. This is the fluid’s secret weapon. As the object pushes into the fluid, it displaces—or moves aside—a certain amount of that fluid. Archimedes, an ancient Greek thinker, discovered that the fluid pushes back with a force equal to the weight of the fluid that was displaced. It’s as if the water is trying to reclaim its space and is shoving the object upward in the process.

The Deciding Factor: A Simple Rule of Density

So, who wins this tug-of-war? The outcome hinges entirely on a single, simple property: density. Density is a measure of how much “stuff” is packed into a given space.

Here’s the golden rule:

• An object will SINK if it is MORE DENSE than the fluid.
• An object will FLOAT if it is LESS DENSE than the fluid.

A Kitchen Sink Experiment

You don’t need a lab to see this in action. Imagine filling your sink with water.

• The Sinking Carrot: Take a solid, dense carrot and drop it in. It sinks straight to the bottom. Why? The carrot is more dense than water. The weight of the carrot (the downward pull) is greater than the maximum upward push the water can provide. Gravity wins decisively.
• The Floating Apple: Now, take an apple and place it in the water. It floats! This is because the apple, with its air-filled structure, is less dense than water. It only needs to displace a small volume of water to generate an upward push that matches its own weight. Once these forces are balanced, it rests comfortably on the surface.
• The Suspended Egg (A Special Case): If you carefully prepare a glass of saltwater, you can make an egg hover in the middle. By adding salt, you increase the water’s density until it matches the density of the egg exactly. When the densities are equal, the upward buoyant force perfectly balances the downward weight, and the object hangs in a state of suspension, neither rising nor falling.

The Magic of Shape: How Steel Ships Float

This leads to a fascinating puzzle: how can a gigantic ship made of dense, heavy steel float, while a tiny steel nail sinks? The secret isn’t in the material itself, but in the object’s average density.

A nail is solid metal. Its density is the density of steel, which is much higher than water.

A ship, however, is not solid. It’s mostly hollow, filled with air. If you take the entire mass of the steel and divide it by the enormous volume of the ship (including all the empty, air-filled space inside), you get an average density. This average density is actually lower than that of water. The ship is shaped to displace a vast amount of water, creating a massive buoyant force that easily supports its weight.

Question 6. 

Explain why an iron nail floats on mercury, but it sinks in water.

Hint : The density of iron is less than that of mercury, but more than that of water. 

Ans:

Whether an object floats or sinks comes down to a simple battle of densities. An object will float if it is less dense than the fluid it is placed in. Think of it as the lighter substance being forced to sit on top of the heavier one.

Let’s apply this rule to the iron nail.

First, consider the nail placed on mercury. The density of iron is approximately 7.8 grams per cubic centimeter (g/cm³). Mercury, however, is far denser, with a density of about 13.6 g/cm³. Since the iron nail is the “lighter” substance in this comparison, it cannot penetrate the much denser liquid metal. The mercury simply cannot make room for the nail to sink, so the nail rests on its surface.

Now, picture the same iron nail dropped into water. The density of water is only 1 g/cm³. In this case, the roles are reversed. The iron nail, at 7.8 g/cm³, is vastly denser than the water surrounding it. The water is the “lighter” substance and is easily pushed aside. The nail’s weight overcomes the water’s ability to support it, causing it to plunge straight to the bottom.

In short:

• On mercury, the nail is like a person on a trampoline that is too firm to bounce; it just stays on top.
• In water, the nail is like a heavy rock thrown into a pond; it immediately breaks the surface and falls because it is the heavier material.

Question 7. 

A body floats in a liquid with a part of it submerged inside the liquid. Is the weight of the floating body greater than, equal to or less than the upthrust?

Ans:

When a body floats steadily in a liquid, the forces acting upon it are perfectly balanced. This is a direct consequence of a fundamental principle of physics.

The weight of the body is the downward force caused by gravity pulling on its mass. The upthrust, also known as the buoyant force, is the upward force exerted by the liquid on the submerged part of the body.

For any object that is stationary and not accelerating—whether it’s sitting on the ground, being held in a hand, or floating—the net force acting on it must be zero. Since the floating body is at rest and not sinking or rising, we can conclude that the upward force and the downward force are in perfect equilibrium.

Therefore, the weight of the floating body is exactly equal to the upthrust provided by the displaced liquid.

Think of it like this: the liquid pushes up with just enough force to cancel out the weight trying to pull the object down. This balance is precisely what allows the body to remain suspended at that particular level without sinking further or bobbing up.

Question 8. 

A homogeneous block floats on water (a) partly immersed (b) completely immersed. In each case state the position of centre of buoyancy B with respect to the centre of gravity G of the block.

Ans:

Step 1: Understanding the Situation

We have a homogeneous block—meaning its density is uniform throughout—floating on water. Two cases are considered:

• (a) The block is partly immersed in water.
• (b) The block is completely immersed in water.

We are to compare the positions of:

• Centre of Buoyancy (B): The point through which the buoyant force acts; it is the centroid of the displaced water volume.
• Centre of Gravity (G): The point through which the weight of the block acts; for a homogeneous block, this is at its geometric center.

Step 2: Case (a) — Partly Immersed

When the block is partly immersed, only a portion of it is below the water surface. The buoyant force acts through the centroid of the submerged volume.

• Since the block is homogeneous, its center of gravity G is at its geometric center.
• The submerged part is typically a section from the bottom upward.
• The centroid of this submerged volume lies below the geometric center of the entire block.

Therefore, in this case:

B is below G

Step 3: Case (b) — Completely Immersed

When the block is completely immersed, the entire volume of the block is underwater. The buoyant force now acts through the centroid of the entire block.

• For a homogeneous block, the centroid of its volume coincides with its center of gravity.

Therefore, in this case:

B and G coincide

​

Final Answers

• (a) Partly immersed: B is below G
• (b) Completely immersed: B and G coincide

Question 9. 

The figure shows the same block of wood floating in three different liquids A, B and C of densities ρ1, ρ2  and ρ3 respectively. Which of the liquids has the highest density? Give a reason for your answer.

Ans:

The behavior of the wooden block in the three liquids reveals a clear winner in the density contest. The block rides highest in Liquid C, sits lower in Liquid B, and sinks deepest in Liquid A.

This entire scene is governed by a fundamental rule of flotation: a floating object pushes aside an amount of liquid that weighs exactly the same as the object itself. Because we are using the same block every time, its weight is a fixed value. This means the buoyant force, which is the upward push from the displaced liquid, must be identical in all three scenarios.

Here is the crucial link: to provide that identical upward force, different liquids must be displaced in different amounts. A dense, heavy liquid is very good at providing push; only a little bit of it is needed to equal the block’s weight. In contrast, a light, less dense liquid is weak at providing support; a much larger amount of it must be moved aside to generate the same lifting power.

Looking at the figure, the block displaces the smallest volume in Liquid C. For a small volume of liquid to have a large enough weight to support the block, that liquid must be very heavy for its size—in other words, it must be very dense.

Therefore, Liquid C is the densest. The block floats high because only a small “portion” of the dense liquid is needed to hold it up. Liquid A, where the block sinks deepest, is the least dense, as a large volume of it is required to match the block’s weight.

Question 10. 

Draw a diagram to show the forces acting on a body floating in water with its some part submerged. Name the forces and show their points of application. How is the weight of water displaced by the floating body related to the weight of the body itself?

Ans:

Forces on a Floating Body

When a body floats in a fluid like water, it is in a state of equilibrium under the action of two main forces. The following is a description of a diagram that illustrates these forces.

Diagram Description:

Imagine a simple rectangular block floating in a container of water. The block is partially submerged, meaning a portion of it is below the water surface and the rest is above.

1. Force of Gravity (Weight): This force acts vertically downward.
   • Point of Application: It is applied at the center of gravity (G) of the entire floating body. This point is typically located at the geometric center for a uniform, regular object like our block.
2. Buoyant Force (Upthrust): This force acts vertically upward.
   • Point of Application: It is applied at the center of buoyancy (B), which is the center of gravity of the volume of water displaced by the body. For the partially submerged block, this point is at the geometric center of the submerged part of the block.

In the diagram, the two forces are represented by arrows:

• An arrow labeled ‘W’ (Weight) pointing downwards from point ‘G’.
• An arrow labeled ‘Fb’ (Buoyant Force) pointing upwards from point ‘B’. For the object to be stable (not rotating), point ‘B’ is usually directly below point ‘G’, and the two arrows are equal in length, signifying they are balanced.

text

   *********************

    *       AIR        *

    *********************  <– Water Surface

    *         |        *

    *         | G      *

    *         |        *  ^

    *——————*  | Submerged Part

    *         |        *  |

    *         | B      *  |

    *         |        *  v

    *********************

          WATER

The Relationship: Archimedes’ Principle

The key to flotation is defined by Archimedes’ Principle. It states that when a body is partially or fully immersed in a fluid, it experiences an upward buoyant force equal to the weight of the fluid it displaces.

For a floating body to be in equilibrium, the net force on it must be zero. Since the only two vertical forces acting on it are its weight (downwards) and the buoyant force (upwards), these two forces must be equal in magnitude and opposite in direction.

Therefore, the relationship is:

The weight of the water displaced by the submerged part of the floating body is exactly equal to the total weight of the body itself.

In simpler terms, the buoyant force pushing up on the object perfectly supports its entire weight, which is why it doesn’t sink. If the object were heavier, it would sink deeper, displacing more water, until the weight of that displaced water once again matched its own weight.

Question 11. 

What is the centre of buoyancy? State its position for a floating body with respect to the centre of gravity of the body. 

Ans:

Think of the centre of buoyancy as the heart of the upward push a floating object experiences. It is defined as the precise point where the total buoyant force acts on a submerged object. This point is located exactly at the center of gravity of the volume of fluid that the object displaces. In simpler terms, if you could take the shape of the pushed-away water and find its balance point, that spot is the centre of buoyancy.

Now, for the relationship with the body’s own centre of gravity (its weight’s balance point):

For a body to float in a stable, upright position, its centre of buoyancy and its centre of gravity must align in a specific vertical relationship. The centre of buoyancy is always positioned directly below the centre of gravity of the floating body.

This arrangement is crucial for stability. It creates a righting lever arm, much like a pendulum. If the floating object tilts, the shape of the displaced fluid changes, causing the centre of buoyancy to shift sideways. This shift creates a turning force that works to rotate the object back to its original, upright position. If the buoyancy centre were above the gravity centre, the slightest tilt would cause the object to flip over uncontrollably.

Question 12. 

A balloon filled with helium gas floats in a big closed jar which is connected to an evacuating pump. What will be your observation, if air from the jar is pumped out? Explain your answer. 

Ans:

Observation and Explanation

If the air is pumped out of the sealed jar, you will observe the helium-filled balloon sinking and eventually resting at the bottom of the jar.

The Explanation: Why Buoyancy Disappears

This surprising result is a direct consequence of how buoyancy works, and it can be understood by breaking down the forces at play.

1. The Principle of Buoyancy: A gas-filled balloon floats in air for the exact same reason a wooden block floats in water: it experiences an upward buoyant force. This force, as established by Archimedes’ principle, is equal to the weight of the fluid (in this case, air) that the balloon displaces.
2. The Balancing Act: Inside the jar, the helium balloon is subject to two main forces:
   • Its own weight (W): The force of gravity pulling it down. This is the combined weight of the helium gas and the balloon’s material.
   • The Buoyant Force (Fb): The upward push from the displaced air.
     The balloon floats because the buoyant force (Fb) is greater than its own weight (W).
3. The Critical Change: Removing the Air: When the air is pumped out of the jar, we are removing the medium in which the balloon is submerged. As the air density decreases:
   • The amount of air available to be displaced by the balloon decreases.
   • Consequently, the weight of that displaced air (the buoyant force) also decreases.
4. The Result: The balloon’s own weight remains constant. However, the supporting buoyant force is rapidly diminishing. At a certain point, when enough air has been removed, the buoyant force will become less than the weight of the balloon. At this moment, the net force is downward, and the balloon will sink, just like a rock in water, until it comes to rest on the bottom of the jar.

Question 13. 

A block of wood is so loaded that it just floats in water at room temperature. What change will occur in the state of floatation, if (a) Some salt is added to water, (b) Water is heated? Give reasons. 

Ans:

The behavior of the block is governed by the delicate balance between its own density and the density of the water it displaces. Since it just floats, its overall density is exactly equal to the density of pure water at room temperature. Any change to the water will disrupt this precise balance.

(a) When salt is added to the water:

A noticeable change occurs: the block of wood will rise slightly so that it floats higher in the water.

The reason for this lies in the water’s increased density. Dissolving salt adds mass to the water without significantly increasing its volume, making the saltwater heavier per cupful. The block’s density, however, remains unchanged. Now, the block finds itself in a fluid that is denser than itself. To achieve a new balance, it does not need to displace as much of this heavier fluid to support its weight. Consequently, a smaller portion of the block remains submerged, and it rides higher in the brine.

(b) When water is heated:

The opposite effect takes place: the block will sink lower, and if heated sufficiently, it may sink completely.

Heating water causes its molecules to move apart, leading to thermal expansion. This expansion means that the same mass of water now occupies a slightly larger volume, resulting in a decrease in its density. The block’s density remains fixed. As the hot water becomes less dense, the block, which was once of equal density to the water, becomes relatively denser than the fluid around it. To keep itself buoyant, it must displace a greater volume of this now-lighter water. This forces more of the block to submerge. If the water is heated enough to reduce its density below that of the wooden block, the block will be denser than the water and will sink entirely.

In summary:

• Salt makes water denser, making the block comparatively lighter and causing it to float higher.
• Heat makes water less dense, making the block comparatively heavier and causing it to float lower or even sink.

Question 14. 

A body of volume V and density ρs , floats with volume v inside a liquid of density ρL. Show that V / 𝑉  = ρ𝑠 / ρ𝐿.

Ans:

Understanding Why Objects Float: A Derivation of the Submerged Volume Ratio

When an object floats, it finds a perfect balance between two competing forces: its own weight pulling it down and the buoyant force of the liquid pushing it up. We can use this balance to derive a simple and powerful relationship between the object’s density, the liquid’s density, and how much of the object sits below the surface.

Question 15. 

Two identical pieces, one of ice (density = 900kg per meter cube) and other wood (density = 300kg per meter cube) float on water. Which of the two will have more volume submerged inside water Which of two will experience more upthrust due to water.

Ans:

To solve this, we need to revisit the core principle of flotation: an object floating freely in a fluid is steadied by an upward push, known as upthrust or buoyant force. The strength of this upward force is exactly equal to the weight of the fluid the object displaces. For a floating object, this upthrust perfectly balances the object’s own weight.

Since both the ice and the wood are identical in size and are floating, they share one crucial characteristic: they both experience the same upthrust.

Why is that? The upthrust must counter their individual weights to keep them afloat. Because the two pieces are identical in volume, the heavier one (with more mass) must be the denser one. Ice, being denser than wood, is therefore heavier for the same size. To support this greater weight, the upthrust on the ice must be stronger.

However, upthrust is generated by the volume of water displaced. A greater upthrust requires a greater volume of water to be pushed aside. Therefore, the heavier and denser piece—the ice—needs to sink deeper into the water to displace a volume of water whose weight equals its own.

The wooden piece, being much lighter for its size, finds a balance by displacing a much smaller amount of water.

In summary:

• Which has more volume submerged? The ice submerges more of its volume. Its higher density requires it to displace more water to achieve the necessary upthrust.
• Which experiences more upthrust? The ice experiences a greater upthrust. This stronger upward force is required to counteract its greater downward weight and keep it floating.

Question 16. 

Why is the floating ice less submerged in brine than in water? 

Ans:

The depth to which ice submerges is a direct result of the liquid’s “lifting power.” Think of the liquid as a support force; a stronger support requires less of the object to be submerged to balance its weight.

Brine, which is water heavily saturated with salt, possesses a greater density than fresh water. The dissolved salt particles increase the mass of the water without significantly increasing its volume, making it a heavier, more robust fluid.

When an object like ice floats, it displaces a volume of liquid equal in weight to the ice’s own weight. Because brine is denser, a smaller volume of it is needed to match the weight of the ice. Imagine trying to balance a one-kilogram block: you would need a larger bowl of light feathers to equal one kilogram, but a much smaller bowl of heavy sand to reach the same weight. The ice is the block, and the brine is the sand.

Therefore, the ice floating on potent brine is buoyed up more forcefully. It does not need to sink as deeply to displace a liquid mass equal to its own. It rides higher in the brine, with a larger portion of its volume remaining proudly above the surface compared to its posture in fresh water.

Question 17. 

A man first swims in sea water and then in river water. (i) Compare the weights of sea water and river water displaced by him. (ii) Where does he find it easier to swim and why? 

Ans:
When a person swims, they float because the water pushes them up with a force equal to the weight of the water their body displaces. This is a fundamental principle of how flotation works. The type of water they are in—whether it’s the sea or a river—plays a significant role in this experience due to one key difference: the density of the water.

Here is a breakdown of the comparison:

(i) Comparison of the Weights of Water Displaced

The weights of the sea water and the river water displaced by the man are identical.

The reason for this is straightforward. The man’s weight remains constant. When he is floating peacefully or swimming, the upward push from the water (the buoyant force) perfectly balances his downward weight. Since this upward force is mathematically equal to the weight of the water he displaces, that displaced weight must be the same in any water body where he is floating. Whether he is in the dense Dead Sea or a less dense freshwater lake, the amount of water he weights is always equal to his own weight.

(ii) Where it is Easier to Swim and Why

The man will find it significantly easier to swim in the sea water.

The explanation lies not in the weight of the displaced water, but in the volume.

• Sea water has a higher density than river water because it contains dissolved salts and minerals. This makes it heavier per cupful, so to speak.
• Because sea water is denser, a smaller volume of it needs to be displaced to achieve a buoyant force equal to the man’s weight.
• In practical terms, this means his body sits higher in the sea water. More of his body is above the surface, and he doesn’t have to work as hard to keep himself from sinking.

Imagine it like this: it’s much easier to float while holding a heavy, dense piece of iron, but much harder to float while holding a large, low-density balloon that displaces the same weight of air. In the sea, the water itself acts like that dense iron, providing more “lift” per liter displaced, making swimming and floating feel more effortless. In river water, his body sinks deeper, requiring more energy and effort to stay afloat and propel himself forward.

Question 18. 

An iron nail sinks in the water while an iron ship floats on water. Explain the reason. 

Ans:

The behavior of the iron nail and the iron ship seems like a complete contradiction, but the secret doesn’t lie in the material itself—it lies in the shape and what that shape encompasses.

Both are made of iron, which is undoubtedly denser than water. A solid nail is a compact piece of iron. Its total weight is concentrated in a small volume, making it heavier than the volume of water it pushes aside. It’s a simple losing battle: a small amount of water cannot hold up the nail’s concentrated weight, so it sinks.

An iron ship, however, is not a solid block of metal. It is a hollowed-out shell. This brilliant engineering trick is the key. While the ship is made of heavy iron, the vast, empty space inside the hull is filled with nothing but air, which is incredibly light.

This means the ship’s total volume—counting all the iron plus all the enclosed air—creates a much larger overall shape. The weight of the ship (the iron and everything in it) is now spread across this huge volume. Crucially, when the ship is placed in water, it displaces a volume of water that is equal to its own total, large volume.

The water pushes back with an upward force (buoyancy) equal to the weight of that displaced water. Because the ship’s hollow shape displaces a massive amount of water, the upward push from the water becomes enormous. For a properly designed ship, this upward force becomes greater than the ship’s total downward weight. The water wins the battle and holds the ship up.

In essence:

• The nail is dense iron versus a small cupful of water. Iron wins, and the nail sinks.
• The ship is a lightweight, air-filled structure versus a colossal volume of water. The water wins, and the ship floats.

Question 19. 

What can you say about the average density of a ship floating on water in relation to the density of water? 

Ans:

It’s a sight that never fails to make one pause: a massive vessel, built from tons of heavy steel, floating effortlessly on the water. Common sense tells us that a solid piece of metal will sink straight to the bottom. So, what is the secret that allows a ship, which is undeniably heavy, to stay afloat? The answer lies not in the weight of the steel, but in the clever use of empty space.

Think of it this way: the force that keeps the ship buoyant is an upward push from the water, created by the volume of water the ship’s hull pushes aside. For the ship to float stably, this upward force must perfectly balance the ship’s downward weight.

This is where the ship’s brilliant design comes into play. A ship is not a solid block of steel; it is essentially a strong, watertight steel shell surrounding a vast amount of air. While the steel itself is dense and heavy, the air trapped inside is incredibly light. If you were to take the entire ship—the steel hull, the engines, the cargo, and all the air inside—and calculate its total mass divided by its total volume, you would arrive at its average density.

This average density is the key. Even though the materials used are dense, the immense volume of the hollow shape dramatically lowers the overall average. Imagine the difference between a solid steel ball and a thin steel bowl. The ball, being solid, has a high average density and will sink. But if you place the bowl gently on the water, it displaces a large volume of water relative to its small weight, and it floats. A ship is simply a giant, scaled-up, and sealed version of that bowl.

So, the ship is engineered to be a hollow object. This design ensures that its average density ends up being less than the density of the water it sits in. It displaces a weight of water equal to its own weight, and in doing so, is held up by the water. It’s a perfect demonstration of a simple principle of physics, harnessed by human ingenuity to achieve the remarkable feat of floating immense structures on the sea.

Question 20. 

A body is held inside water contained in a vessel by tying it with a thread to the base of the vessel. Name the three forces that keep the body in equilibrium, and state the direction in which each force acts. 

Ans:

1. The Downward Pull of Its Own Heaviness (Gravity’s Effect)
The first force is the object’s weight. This is the relentless, downward pull caused by the Earth’s gravity acting on the object’s mass. It is a constant force, always trying to drag the object straight to the bottom of the container.

2. The Upward Push from the Displaced Water (The Water’s Lift)
The second force is buoyancy. By simply occupying space underwater, the object displaces a certain volume of water. The surrounding water reacts by pushing back against the object with an upward force. This supportive lift is what makes some objects feel lighter when submerged.

3. The Upward Tug of the Tether (The Thread’s Restraint)
The third force is the tension in the thread. Since the object’s own weight is greater than the water’s buoyant lift, it would naturally sink. The thread, anchored firmly to the base, prevents this. It pulls upward on the object, supplying the precise amount of additional force needed to counteract the remaining downward pull.

In essence, the object remains motionless because the two upward forces—the water’s buoyant push and the thread’s taut pull—together perfectly balance the single, persistent downward force of the object’s weight.

Question 21. 

A loaded cargo ship sails from sea water to river water. State and Explain your observations. 

Ans:

Observing a Cargo Ship Moving from Sea to River Water

When a loaded cargo ship sails from the open sea into a river, a careful observer will notice a distinct change: the ship will sit lower in the water, meaning its hull sinks deeper as it moves into the river.

This seemingly simple observation is driven by a fundamental scientific principle known as Archimedes’ principle. This principle states that any floating object displaces a volume of fluid whose weight is equal to the object’s own weight.

Let’s break down why this leads to the ship sinking deeper:

1. The Constant Factor: The Ship’s Weight. The cargo ship, along with its load, has a fixed total weight. For the ship to float, the upward push (buoyant force) from the water must exactly balance this weight, regardless of whether it is in sea water or river water.
2. The Changing Factor: Water Density. This is the key to the entire phenomenon. Sea water is denser than fresh river water. This is because sea water contains a significant amount of dissolved salts and minerals, which make it heavier for the same volume.
3. The Relationship Between Density and Displacement. Since the buoyant force must always equal the ship’s constant weight, the ship must displace the same weight of water in both environments. However, because river water is less dense (lighter per cubic meter), the ship needs to displace a larger volume of it to equal the same weight.
4. The Visible Result: Deeper Draught. To displace this larger volume of lighter river water, the ship must sink deeper into the river, pushing more of its hull underwater. This increase in the depth of the submerged part of the hull is known as an increase in its “draught.”

Question 22. 

A piece of ice floating in a glass of water melts, but the level of water in the glass does not change. Give reasons.Hint: Ice contracts on melting. 

Ans:

This is a classic observation that seems counterintuitive at first glance. The reason the water level remains unchanged is rooted in a specific principle of buoyancy and the unique property of water.

Here’s the breakdown:

When the piece of ice is floating, it is already displacing a certain volume of water. The crucial law at play is Archimedes’ principle, which tells us that a floating object displaces a volume of water whose weight is equal to the object’s own weight.

So, the floating ice block pushes aside an amount of water that weighs exactly the same as the entire ice block.

Now, what happens when the ice melts? It transforms from a solid state into a liquid state. The key is that the mass of the water produced from the melting ice is identical to the mass of the original ice block. Since density is mass per unit volume, this newly formed liquid water will occupy a volume precisely equal to the volume of water that was originally displaced.

Think of it as a perfect trade:

• The ice, while floating, claimed a “water space” in the glass by displacement.
• Upon melting, the ice simply fills that exact same “water space” itself, as liquid water.

Therefore, there is no net addition or subtraction to the overall volume of water in the glass. The level remains perfectly steady.

Regarding the hint about ice contracting: This is the fundamental reason this works for water and not for most other substances. For most materials, the solid is denser than the liquid. However, water is special—ice is less dense than liquid water. This expansion upon freezing is the very reason ice floats. When that same ice melts, it contracts back into the more compact liquid form, and this contraction perfectly matches the volume it was already occupying through displacement. If ice were denser than water (like a metal), it would sink and the melting process would cause the water level to change.

Question 23. 

1. Explain the following : Icebergs floating in sea are dangerous for ships.

2. Explain the following : An egg sinks in fresh water, but floats in a strong salt solution.

3. Explain the following : Toy balloons filled with hydrogen rise to the ceiling, but if they are filled with carbon dioxide, then they sink to the floor. 

4. Explain the following : As a ship in harbour is being unloaded, it slowly rises higher in water. 

5. Explain the following : A balloon filled with hydrogen rises to a certain height and then stops rising further.

6. Explain the following : A ship submerges more as it sails from sea water to river water.

Ans:

1. Icebergs floating in the sea are dangerous for ships.

This danger stems from the deceptive nature of how icebergs float. Ice is less dense than liquid water, which is why it floats. However, a vast majority of an iceberg’s bulk is hidden beneath the water’s surface. Typically, only about one-tenth of an iceberg is visible above water, while the remaining nine-tenths lurk underwater. This large, submerged portion is often much wider than the visible tip and can be sharp and jagged. Since a ship’s hull extends deep into the water, it can collide with this unseen, underwater part of the iceberg long before the ship gets close to the visible section, leading to potential punctures and sinking.

2. An egg sinks in fresh water, but floats in a strong salt solution.

This happens because of changes in the water’s density. An egg is slightly denser than fresh water, meaning it weighs more for its size. As a result, it sinks. When a large amount of salt is dissolved in the water, the salt ions fill the spaces between the water molecules, making the solution denser without significantly increasing its volume. A strong salt solution can become denser than the egg. When this happens, the buoyant force pushing the egg upward becomes greater than the weight of the egg pulling it downward, causing it to float.

3. Toy balloons filled with hydrogen rise to the ceiling, but if filled with carbon dioxide, they sink to the floor.

This is all about the relative density of the gases inside the balloons compared to the surrounding air. The air in our atmosphere is a mixture of gases, primarily nitrogen and oxygen. Hydrogen gas is much less dense (lighter) than this atmospheric air. Therefore, a hydrogen-filled balloon is lighter than the air it displaces, causing it to rise. Carbon dioxide (CO₂), on the other hand, is a heavier gas and is denser than air. A balloon filled with CO₂ is heavier than the air it displaces, so the force of gravity pulls it down, making it sink to the floor.

4. As a ship in harbour is being unloaded, it slowly rises higher in water.

This is a direct demonstration of Archimedes’ principle. A floating ship displaces a volume of water that weighs the same as the entire ship, including its cargo. When cargo is unloaded, the ship’s total weight decreases. To maintain this balance, the ship no longer needs to displace as much water. It therefore rises in the water until the weight of the displaced water once again equals the new, lighter weight of the ship. It’s like a heavily laden canoe sitting low in the water; when you step out, it rises noticeably.

5. A balloon filled with hydrogen rises to a certain height and then stops rising further.

While hydrogen is lighter than air at ground level, the atmosphere changes with altitude. As the balloon rises, the atmospheric pressure decreases, allowing the gas inside the balloon to expand. The balloon itself can only stretch so far. Eventually, it reaches an altitude where it can no longer expand, and the density of the hydrogen inside becomes equal to the density of the thinner, less dense air outside. At this point of neutral buoyancy, the balloon is no longer lighter than its surroundings and stops rising. Additionally, if it’s a flexible balloon, it might even burst from the pressure difference.

6. A ship submerges more as it sails from sea water to river water.

The key difference is the density of the water. Sea water contains dissolved salts and minerals, making it denser than fresh river water. A floating ship displaces its own weight in water. In denser sea water, it needs to displace a smaller volume to achieve this balance, so it floats higher. When it moves into less dense fresh water, it must displace a larger volume of water to equal its weight. To displace this larger volume, the ship sinks deeper into the water.

Exercise 5 (C)

Question 1. 

For a floating body, its weight W and upthrust FB on it are related as :

1. W > FB
2. W < FB
3. W = FB
4. Nothing can be said

Question 2. 

A body of weight W is floating in a liquid. Its apparent weight will be

1. Equal to W
2. Less than W
3. Greater than W
4. Zero

Question 3. 

A body floats in a liquid A of density ρ1 with a part of it submerged inside the liquid, while in liquid B of density ρ2 it is totally submerged inside the liquid. The densities ρ1 and ρ2 are related as : 

1. ρ1 = ρ2 
2. ρ1 < ρ2
3. ρ1 > ρ2
4. Nothing can be said

Exercise 5 (C)

Question 1. 

A rubber ball floats on water with its 1/3rd volume outside water. What is the density of rubber? 

Ans:

Question 2. 

A block of wood of mass 24 kg floats on water. The volume of wood is 0.032 m3. Find: 

the volume of blocks below the surface of water, the density of wood. (Density of water = 1000 kg m−3)

Ans:

Question 3. 

A wooden cube of 10 cm has a mass 700 g. What part of it remains above the water surface while floating vertically on the water surface? 

Ans:

Question 4. 

A piece of wax floats on brine. What fraction of its volume is immersed?

Density of wax = 0.95 g cm-3, Density of brine = 1.1 g cm-3. 

Ans:

When an object floats, it pushes aside a volume of fluid equal in weight to its own. This principle allows us to solve for the submerged portion of the wax.

The weight of the entire wax piece is its density multiplied by its total volume and gravity:
Weight of wax = ρ_wax × V_total × g

The buoyant force supporting it is the weight of the brine it displaces. This depends on the immersed volume:
Weight of displaced brine = ρ_brine × V_immersed × g

Since the wax floats calmly, these two forces are in balance:
ρ_wax × V_total × g = ρ_brine × V_immersed × g

We can simplify this by canceling the ‘g’ from both sides, leaving:
ρ_wax × V_total = ρ_brine × V_immersed

Our goal is to find the fraction of the volume that is immersed, which is V_immersed / V_total. Rearranging the equation gives us this exact ratio:

V_immersed / V_total = ρ_wax / ρ_brine

Now we substitute the given values:
Density of wax (ρ_wax) = 0.95 g/cm³
Density of brine (ρ_brine) = 1.1 g/cm³

Fraction immersed = 0.95 / 1.1

Calculating this gives:
Fraction immersed = 95/110 = 19/22

Question 5.

If the density of ice is 0.9 g cm-3, then what portion of an iceberg will remain below the surface of water in sea? (Density of sea water = 1.1 g cm-3) 

Ans:

Understanding How Much of an Iceberg is Underwater

Have you ever looked at a picture of an iceberg and wondered just how much of it is hidden beneath the ocean’s surface? The answer lies in a beautiful and fundamental concept of physics discovered by Archimedes. Let’s explore this step-by-step, focusing on the logic behind the calculation.

The Key Idea: A Balancing Act of Weight

At its heart, the reason an iceberg floats is due to a perfect balance of forces. Archimedes’ principle tells us that the weight of the water pushed aside (displaced) by the submerged part of the iceberg must exactly equal the total weight of the entire iceberg itself. Think of it as the ocean providing an upward push strong enough to support the iceberg’s total mass.

Setting the Stage with Densities

To put numbers to this idea, we need two key pieces of information:

1. Density of Ice: The iceberg itself is made of ice, which has a density of approximately 0.9 grams per cubic centimeter.
2. Density of Sea Water: The ocean is not pure water; it’s salt water, which is denser. A typical value for sea water density is 1.1 grams per cubic centimeter.

Building the Equation

Let’s define our terms:

• Let V_total represent the total volume of the entire iceberg.
• Let V_sub represent just the volume of the iceberg that is submerged underwater.

Question 6. 

A piece of wood of uniform cross section and height 15 cm floats vertically with its height 10 cm in water and 12 cm in spirit. Find the densities of wood and spirit. 

Ans:

Question 7. 

A wooden block floats in water with two-third of its volume submerged.

(a) Calculate the density of wood. 

(b) When the same block is placed in oil, three-quarters of its volume is immersed in oil. Calculate the density of oil. 

Ans:

Solving the Wood and Oil Density Problem

This problem uses Archimedes’ principle, which states that the buoyant force on an object is equal to the weight of the fluid displaced by the object. For a floating object, the buoyant force exactly balances the object’s weight.

Question 8. 

The density of ice is 0.92 g cm-3 and that of sea water is 1.025 g cm-3. Find the total volume of an iceberg which floats with its volume 800 cm3 above water.

Ans:

When an object floats, it pushes aside a volume of fluid whose weight is exactly equal to the object’s own weight. This is the key principle we will use.

Let’s define our terms:

• Density of Ice, ρ_ice = 0.92 g/cm³
• Density of Sea Water, ρ_water = 1.025 g/cm³
• Volume above water, V_above = 800 cm³
• Volume below water, V_below = ? (This is what we need to find first)
• Total Volume of Iceberg, V_total = ? (This is our final goal)

Step 1: Understanding the Flotation

The total volume of the iceberg (V_total) is the sum of the part we see and the submerged part:
V_total = V_above + V_below

The weight of the entire iceberg is its density multiplied by its total volume and gravity (g):
Weight of Iceberg = ρ_ice * V_total * g

According to the flotation principle, this weight is supported by the weight of the seawater displaced. The iceberg only displaces a volume of water equal to its submerged portion, V_below.

Therefore, the Buoyant Force (weight of displaced water) is:
Buoyant Force = ρ_water * V_below * g

Since the iceberg is floating in equilibrium:
Weight of Iceberg = Buoyant Force
ρ_ice * V_total * g = ρ_water * V_below * g

We can cancel the gravitational acceleration ‘g’ from both sides, simplifying our working equation to:
ρ_ice * V_total = ρ_water * V_below …(Equation 1)

Step 2: Substituting and Solving

We know that V_total = V_above + V_below. Let’s substitute this into Equation 1.

ρ_ice * (V_above + V_below) = ρ_water * V_below

Now, plug in the known values:
0.92 * (800 + V_below) = 1.025 * V_below

Let’s solve for V_below:
0.92*800 + 0.92*V_below = 1.025*V_below
736 + 0.92 V_below = 1.025 V_below
736 = 1.025 V_below – 0.92 V_below
736 = 0.105 V_below
V_below = 736 / 0.105
V_below ≈ 7009.52 cm³

Step 3: Finding the Total Volume

Now that we know the volume of the submerged portion, finding the total volume is straightforward.

V_total = V_above + V_below
V_total = 800 cm³ + 7009.52 cm³
V_total ≈ 7809.52 cm³

Final Answer:

The total volume of the iceberg is approximately 7,810 cm³.

Question 9. 

A weather forecasting plastic balloon of volume 15 m3 contains hydrogen of density 0.09 kg m-3. The volume of equipment carried by the balloon is negligible compared to its own volume. The mass of an empty balloon alone is 7.15 kg. The balloon is floating in air of density of 1.3 kg m-3. Calculate:

(i) The mass of hydrogen in the balloon,

(ii) The mass of hydrogen and balloon,

(iii) The total mass of hydrogen, balloon and equipment if the mass of equipment is x kg,

(iv) The mass of air displaced by balloon and

(v) The mass of equipment using the law of floatation.

Ans:

Analyzing the Weather Balloon’s Payload Capacity

Let’s work through this problem step-by-step to find out how much equipment the weather balloon can carry. The key to solving this is understanding the principle of flotation: an object will float when its total weight is balanced by the upward push (buoyant force) of the displaced air.

Step 1: Finding the Mass of the Hydrogen Gas

First, we determine the mass of the gas filling the balloon. We use the basic formula connecting mass, density, and volume.

• Volume of hydrogen: 15 m³
• Density of hydrogen: 0.09 kg/m³

Calculation:
Mass of Hydrogen = Density × Volume
= 0.09 kg/m³ × 15 m³
= 1.35 kg

(i) The mass of hydrogen is 1.35 kg.

Step 2: Calculating the Combined Mass of the Balloon and its Gas

Before adding any equipment, we find the mass of the balloon structure and the hydrogen inside it.

• Mass of empty balloon: 7.15 kg
• Mass of hydrogen: 1.35 kg

Calculation:
Mass of Balloon & Hydrogen = 7.15 kg + 1.35 kg
= 8.50 kg

(ii) The total mass of the hydrogen and the balloon is 8.50 kg.

Step 3: Establishing the Total Mass of the Entire Floating System

Now we include the unknown mass of the equipment, which we’ll call *x* kilograms. This gives us the total mass that the buoyant force must support.

Total Mass = Mass of (Balloon + Hydrogen + Equipment)
= 8.50 kg + *x* kg

(iii) The total mass is (8.50 + *x*) kg.

Step 4: Determining the Mass of the Displaced Air

According to Archimedes’ principle, the buoyant force is equal to the weight of the air the balloon pushes aside. Since the balloon fully inflates the space, it displaces a volume of air equal to its own volume.

• Volume displaced: 15 m³
• Density of air: 1.3 kg/m³

Calculation:
Mass of Displaced Air = Density of Air × Volume
= 1.3 kg/m³ × 15 m³
= 19.5 kg

(iv) The mass of the air displaced is 19.5 kg.

Step 5: Applying the Law of Floatation to Find the Equipment Mass

For the balloon to float in equilibrium, the total weight of the entire system must be exactly equal to the weight of the displaced air. Since weight is mass multiplied by gravity (g), we can simplify the equation by dividing both sides by g. This leaves us with a balance of masses.

The Floatation Condition:
Total Mass of System = Mass of Displaced Air

Substituting the values we found:
8.50 + *x* = 19.5

Now, solving for *x*:
*x* = 19.5 – 8.50
*x* = 11.0 kg

(v) The mass of the equipment the balloon can carry is 11.0 kg.

Summary of Final Answers:

• (i) 1.35 kg
• (ii) 8.50 kg
• (iii) (8.50 + *x*) kg
• (iv) 19.5 kg
• (v) 11.0 kg