Refraction of Light at Plane Surface 

1. What is Refraction?

Refraction is the bending of light as it passes at an angle from one transparent material (like air) into another (like water or glass). This happens because light changes speed in different materials.

2. Why and How Does Light Bend?

Light slows down when entering a denser medium (like air to water), causing it to bend towards the normal (an imaginary perpendicular line).

Light speeds up when entering a rarer medium (like water to air), causing it to bend away from the normal.

3. Snell’s Law

This law states that for two specific materials, the ratio sini/sinris a constant, known as the refractive index (n). Here, 

i is the angle of incidence and 

r is the angle of refraction.

4. Refractive Index

The refractive index measures how much a material bends light. It’s defined as 

n=c/v , where 

c is light’s speed in a vacuum and 

v is its speed in the material. A higher index means more bending.

5. Real-Life Effect: Apparent Depth

An object under water looks closer to the surface than it really is. This is because the light rays bend as they leave the water, and our brain misjudges their origin. The refractive index can be calculated as 

n=Real Depth/Apparent Depth

6. Total Internal Reflection (TIR)

This occurs when light tries to move from a denser to a rarer medium (e.g., from water to air).

Critical Angle: The specific angle inside the denser material where the light ray refracts at exactly 90°.

If the light hits the boundary at an angle larger than this critical angle, it doesn’t escape. Instead, it gets completely reflected back inside. This is Total Internal Reflection.

7. Uses of Total Internal Reflection

TIR is used in many technologies:

Optical Fibres: Thin glass wires that guide light for internet and TV signals.

Prisms: Used in binoculars to reflect light and make the device shorter.

Diamonds: Their brilliant sparkle comes from cutting them to trap light via TIR.

Mirages: The “puddles” seen on hot roads are caused by TIR in layers of hot and cool air.

EXERCISE – 4 (A)  

Question 1: What do you understand by refraction of light? 

Ans:Refraction of light is the bending of light rays when they pass from one transparent medium into another.This bending happens because light changes speed as it moves between substances of different densities, like from air into water or glass.

Question 2: Draw diagrams to show the refraction of light from (i) air to glass, (ii) glass to air. In each diagram, label the incident ray, refracted ray, the angle of incidence (i) and the angle of refraction (r). 

Ans: (i) Refraction from Air to Glass

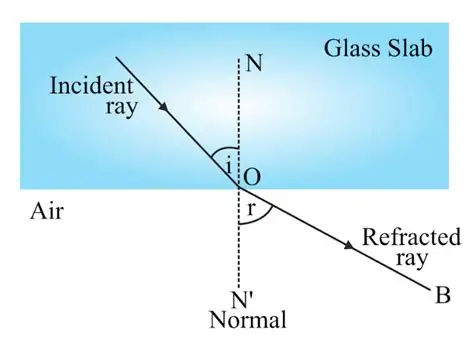
Bending of Ray: The ray bends towards the normal.

Reason: Glass is optically denser than air.

Angle Relationship: Angle of incidence (i) > Angle of refraction (r).

(ii) Refraction from Glass to Air

Bending of Ray: The ray bends away from the normal.

Reason: Air is optically rarer than glass. Light speeds up when entering a rarer medium, causing it to bend away from the normal.

Angle Relationship: Angle of incidence (i) < Angle of refraction (r).

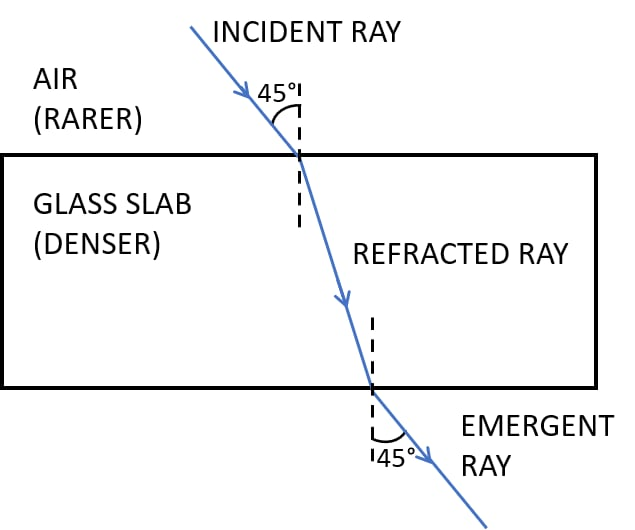
Question 3: A ray of light is incident normally on a plane glass slab. What will be (i) the angle of refraction and (ii) the angle of deviation for the ray? 

Ans:  When a ray of light is incident normally on a surface, it means the ray is perpendicular to the surface, striking it at a 90-degree angle.

(i) Angle of Refraction

The angle of refraction is the angle between the refracted ray inside the medium and the normal to the surface.

Since the incident ray is perfectly perpendicular (along the normal itself), it enters the glass slab without bending. This is because the component of the light’s velocity parallel to the interface is zero when it hits normally. Therefore, the ray continues to travel in a straight line into the glass.

Hence, the refracted ray will also lie along the normal. The angle between the refracted ray and the normal is 0°.

(ii) Angle of Deviation

The angle of deviation is the angle between the direction of the emergent ray and the direction of the original incident ray.

In this case:

The incident ray enters normally and goes straight in.

It then travels through the glass and emerges from the other parallel side of the slab.

For a parallel-sided slab, when a ray emerges into the original medium (air), it undergoes a second refraction. However, because the incident ray was normal to the first surface, it is also normal to the second surface. As a result, it emerges straight without any bending.

The emergent ray is parallel to the incident ray, meaning there is no change in its path.

Therefore, the angle between the original incident ray and the final emergent ray is 0°.

Question 4: What is the cause of refraction of light when it passes from one medium to another? 

Ans:  Light refracts, or bends, because its speed changes when it moves between different transparent materials, like from air to water.Think of it like a shopping cart: if you push it at an angle from a smooth floor onto a rough carpet, one wheel hits the carpet first and slows down. The other wheels, still on the smooth floor, are moving faster. This speed difference causes the cart to turn.Light acts similarly. When it enters glass or water at an angle, one side of the light wave slows down first while the other side is still moving fast. This makes the entire light ray change direction and bend.

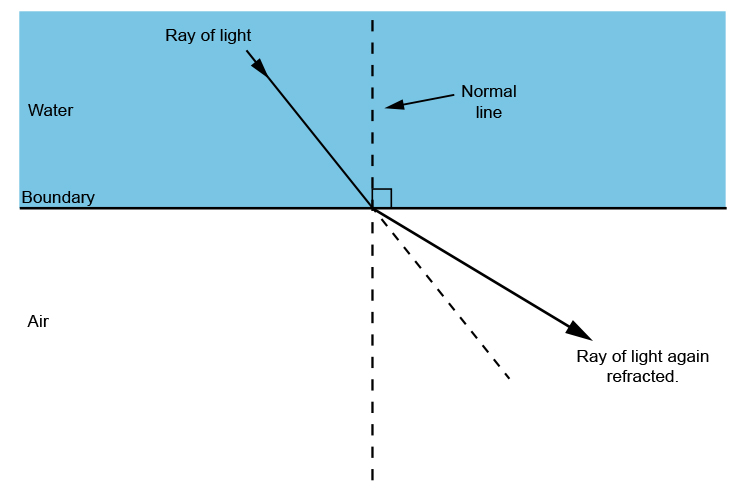
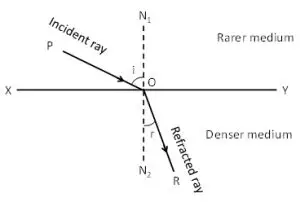
Question 5: A light ray suffers reflection and refraction at the boundary in passing from air to water. Draw a neat labelled ray diagram to show it. 

Ans: A neat labelled ray diagram would show:

Air (rarer medium) above the boundary line.

Water (denser medium) below the boundary line.

An incident ray from air striking the boundary at point of incidence.

A reflected ray bouncing back into air, making an angle equal to the angle of incidence.

A refracted ray bending towards the normal as it enters water.

The Normal, a perpendicular line to the boundary at the point of incidence.

Angle of incidence (∠i), Angle of reflection (∠r), and Angle of refraction (∠R) clearly marked.

Key Observation: ∠i = ∠r, and ∠R < ∠i.

Question 6: A ray of light passes from medium 1 to medium 2. Which of the following quantities of the refracted ray will differ from that of the incident ray: Speed, intensity, frequency, wavelength? 

Ans: Speed and wavelength of the refracted ray will differ from the incident ray.

Frequency remains the same.

Intensity generally decreases due to reflection at the interface and possibly absorption, but the core physical quantities that always change during refraction are speed and wavelength.

Question 7: State the snell’s laws of refraction of light. 

Ans: Snell’s Law of Refraction

Snell’s Law describes how light bends, or refracts, when it crosses from one material into another (like from air into water).

The core idea is this formula:

n₁ sin(i) = n₂ sin(r)

Here’s what the terms mean:

i is the angle of incidence—the angle the incoming light ray makes with an imaginary perpendicular line (called the “normal”).

r is the angle of refraction—the angle the bent light ray makes inside the new material.

In simple terms: The formula lets you calculate the exact angle that light will bend when it enters a new substance like glass or water.

Question 8: Define the term refraction index of a medium. Can it be less than 1? 

Ans:  The refractive index compares the speed of light in a vacuum to its speed in a material. It is usually greater than 1 because light travels slower in most substances.

However, a refractive index of less than 1 is possible in specific cases, like certain plasmas or engineered metamaterials. This occurs when the light’s phase velocity temporarily exceeds the vacuum speed of light.Crucially, this does not break the laws of physics. The phase velocity is not the speed of information. Any actual signal travels at the group velocity, which always remains less than the speed of light in a vacuum.

Question 9: How is the refractive index of a medium related to the speed of light in it? 

Ans: The refractive index is a direct measure of how much a material slows down light.

It is defined by a simple formula: n = c / v

n is the refractive index.

c is the speed of light in a vacuum (its universal top speed).

v is the slower speed of light inside the material.

What this means in practice:

A higher refractive index means light is slowed down more. For example, diamond has a very high index of about 2.42, meaning light travels over twice as slow in diamond as it does in a vacuum.

A lower refractive index means light is slowed down less. Air, for instance, has an index very close to 1, so light travels through it at almost its vacuum speed.

This slowing effect is the fundamental reason why light bends, or refracts, when it enters a material like water or glass at an angle. In short, the refractive index is a direct rating of a material’s “light-slowing power.”

Question 10: A light ray passes from to (a) air, (b) glass. In each case state, how does the speed of light change. 

Ans:  (a) From air to glass:

When a ray of light travels from air into a piece of glass, its speed immediately decreases. Think of it like a car moving from a smooth, open highway (air) onto a rough, gravel road (glass). The glass is a denser medium, meaning its atoms are packed more tightly together. As the light wave enters this crowded environment, it constantly interacts with these atoms—being absorbed and re-emitted by them. This process, while incredibly fast, creates a kind of resistance that slows the overall forward progress of the light wave. This is why light travels slower in glass than in air.

(b) From glass to air:

Conversely, when light emerges from glass back into air, its speed increases. Using the same analogy, it’s like the car is now accelerating off the rough gravel road and back onto the smooth highway. The air is a less dense medium, with far fewer atoms for the light to interact with. With these obstacles removed, the light wave can travel with much less interruption, allowing it to speed up and regain its original, faster velocity through the air.

 Question 11: A light ray in passing from water to a medium (a) speeds up (b) slows down. In each case, give one example of the medium. 

Ans: The behavior of a light ray when it passes from water into another medium depends on the optical density of that new medium.

(a) Speeds Up

If the light ray speeds up, it means it is entering a medium that is optically less dense than water. In such a case, the light ray will bend away from the normal line (the perpendicular line to the surface).

Example of the medium: Air

When a light ray emerges from water into the air, it travels faster because air is much less dense than water. This is why a straw in a glass of water looks bent at the surface.

(b) Slows Down

If the light ray slows down, it means it is entering a medium that is optically denser than water. In this situation, the light ray will bend towards the normal line.

Example of the medium: Glass

When a light ray passes from water into a piece of glass (like a glass aquarium wall), it slows down because common glass has a higher optical density than water.

Question 12: How does the speed of light change when it passes from glass to water? 

Ans:  Think of light as a runner. Different materials, like glass and water, are like different types of terrain. Glass is a “denser” optical medium, which is like thick, muddy ground that slows the runner down. Water is a “less dense” optical medium compared to glass, which is like a wet but firmer track.

Since the runner (light) is moving from a slower terrain (glass) to a faster one (water), it naturally speeds up.

To put it more scientifically, every material has an “optical density” which is measured by its refractive index. Glass has a higher refractive index (around 1.5) than water (around 1.3). The speed of light in any material is given by the formula: Speed in medium = (Speed in vacuum) / (Refractive Index).

Because the refractive index of water is lower than that of glass, the value we divide by gets smaller. So, the speed of light becomes greater when it enters water from glass.

Question 13: A ray of light is passing from a transparent medium 1 to another transparent medium 2 (i) Speed up (ii) slows down. In each case, state whether the refractive index of medium 2 is equal to, less than or greater than the refractive index 

Ans: The refractive index (*n*) of a material tells us how much it slows down light. It’s defined as *n* = c / v, where *c* is the speed of light in a vacuum and *v* is its speed in the material. Since light travels fastest in a vacuum, *v* is always less than *c*, making *n* always greater than 1 for any substance.

(i) If the ray speeds up in medium 2, then n₂ < n₁.

When light speeds up entering a new medium, it means that medium is less optically dense. According to the formula *n* = c / v, a higher speed (*v*) results in a lower refractive index (*n*). Therefore, the refractive index of medium 2 must be lower than that of medium 1.

Example: Light moving from water into air speeds up and bends away from the normal line.

(ii) If the ray slows down in medium 2, then n₂ > n₁.

When light slows down, it means the new medium is more optically dense. A lower speed (*v*) directly results in a higher refractive index (*n*). Therefore, the refractive index of medium 2 is greater than that of medium 1.

Example: Light moving from air into glass slows down and bends towards the normal line.

Question 14: What do you understand by the statement the refractive index of glass is 1.5 for white light? 

Ans: The statement “the refractive index of glass is 1.5 for white light” is a general average.

It means that when white light (which is a mixture of all colors) passes from air into glass, it bends, or refracts.

The number 1.5 indicates that light travels 1.5 times slower in glass than it does in a vacuum (or approximately air). In simpler terms, the speed of light in glass is about two-thirds of its speed in air.

Since white light is made of different colors, and each color bends by a slightly different amount, 1.5 is not a perfect number for every single color. It is a convenient average value used for calculations where extreme precision for a specific color is not needed.

Question 15: A monochromatic ray of light passes from air to glass. The wavelength of light in air is λ, the speed of light in air is c and in glass is ν. If the absolute refractive index of glass is 1.5, write down (a) the relationship between 𝒸 and ν, (b) the wavelength of light in glass. 

Ans: (a) Relationship between c and ν

The absolute refractive index (n) of a medium is defined as the ratio of the speed of light in a vacuum (or air, as a very close approximation) to its speed in that medium. This gives the fundamental relationship:

n = c / ν

Given that the refractive index of glass is 1.5, the relationship between the speed of light in air (c) and in glass (ν) is:

c = 1.5 ν

or, equivalently,

ν = c / 1.5

This shows that the speed of light in glass (ν) is reduced to two-thirds of its speed in air.

(b) Wavelength of light in glass

However, since the wave speed changes (v = fλ), the wavelength must change proportionally to the speed. The wavelength in a medium (λ_m) is related to the wavelength in air (λ) by the refractive index:

λ_glass = λ / n

Substituting the given value of n = 1.5, the wavelength of light in the glass is:

λ_glass = λ / 1.5

This means the wavelength of light is also reduced to two-thirds of its original wavelength in air when it enters the glass.

Question 16: For which colour of white light, is the refractive index of a transparent medium (a) the least (b) the most? 

Ans:  (a) Least Refractive Index: Red Colour

When a beam of white light, which is a mixture of all colours, enters a transparent material like glass, it slows down and bends. This bending is called refraction. We measure how much a material bends light using its refractive index.

Red light has the longest wavelength and the lowest frequency among the visible colours. Because of these specific properties, red light interacts a bit less strongly with the atoms of the material. It is slowed down less compared to other colours and consequently bends the least as it enters the medium. Since the refractive index is a measure of how much the light is bent, red light experiences the least refractive index.

(b) Greatest Refractive Index: Violet Colour

On the opposite end of the visible spectrum, we have violet light. This high energy causes it to interact more intensely with the electrons in the material. As a result, violet light is slowed down the most dramatically. This greater slowing leads to a sharper bend when it enters the medium. Therefore, because it is bent the most, violet light experiences the greatest refractive index.

 Question 17: Name two factors on which the refractive index of a medium depends? State how does it depend on the factors stated by you. 

Ans: 1. Nature of the Medium (Density):

The refractive index depends on the optical density of the material. Generally, for a rarer medium (like gases), the refractive index is lower, while for a denser medium (like solids or liquids), it is higher. For example, the refractive index of glass is about 1.5, while that of water is about 1.33. This is because a denser medium has more particles per unit volume, which slows down light more effectively, increasing the refractive index.

2. Wavelength of Light (Colour):

The refractive index of a medium is inversely related to the wavelength of the incident light. It decreases with an increase in wavelength. This is why different colours of light bend by different amounts when passing through a prism—a phenomenon known as dispersion. For instance, violet light (shorter wavelength) bends more than red light (longer wavelength) in glass.

Question 18: How does the refractive index of a medium depend on the wavelength of light used? 

Ans:The refractive index of a medium depends on the wavelength of light through a phenomenon called dispersion. In general, the refractive index decreases as the wavelength of light increases.This means that shorter wavelengths of light, like blue and violet, are bent more when passing through a medium. Conversely, longer wavelengths, like red and orange, are bent less. This is why white light splits into its constituent colours when it passes through a prism; each colour has a different wavelength and thus experiences a different refractive index.

 Question 19: How does the refractive index of a medium depend on its temperature?  

Ans: The refractive index of a medium typically decreases with an increase in temperature.This happens because as the temperature rises, most materials expand. This expansion decreases the density of the medium, meaning there are fewer atoms or molecules per unit volume to interact with and slow down the light. Since the refractive index is a measure of how much a medium slows down light, a lower density results in a smaller refractive index. For gases, this change is quite significant, while for solids and liquids, the effect is smaller but still measurable. This principle is crucial in applications like correcting for thermal lensing in high-power lasers and in precision optical instruments.

Question 20: A ray of light from air suffers partial reflection and refraction at the boundary of water. In Fig. 4.16, which of the ray A, B, C, D and E is the correct (i) refracted ray (ii) partially reflected ray? 

Ans:  (i) The correct refracted ray is C. This is because when light enters water from air, it bends towards the normal due to water’s higher optical density.

(ii) The correct partially reflected ray is B. This ray obeys the law of reflection, where the angle of reflection equals the angle of incidence.

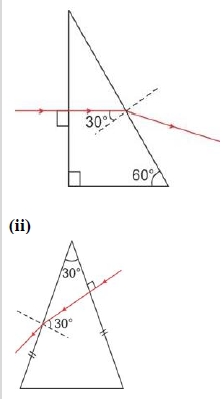
Question 21: The diagram alongside shows the refraction of a ray of light from sir to a liquid. (a) write the values of (i) angle of incidence, (ii) angle of refraction. (b) use snell’s law to find the refractive index of liquid with respect to air.  

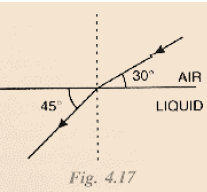
Ans: (a) Values of angles

(i) Angle of incidence = 60°

(ii) Angle of refraction = 45°

(b) Refractive index using Snell’s law

Snell’s law states:

n1sini=n2sinr

Here, 

n1≈1 for air, i=60 ∘ , r=45 ∘ .

n2=sini/sinr

=sin60∘/sin45∘

n2= ≈1.2247

So, the refractive index of the liquid with respect to air is approximately 1.22.

Question 22: The refractive index of water with respect to air is a μ w and of glass with respect to air is a μ g. express the refractive index of glass with respect to water.  

Ans: 

The refractive index of glass with respect to water is denoted as wμg.

It is calculated using the formula:

wμg = (aμg) / (aμw)

Here, aμg is the refractive index of glass with respect to air, and aμw is the refractive index of water with respect to air.

Thus, the refractive index of glass with respect to water is simply the ratio of the refractive index of glass to that of water, both taken with respect to air.

Question 23: In fig , name the ray which represents the correct path of light while emerging out through a glass block.  

 

Ans:  In the given figure, the correct path of light emerging from a glass block is represented by Ray A.This is because when a light ray passes through a parallel-sided glass block, it undergoes refraction. It bends towards the normal when entering the denser glass medium and bends away from the normal when exiting back into the air. For the emergent ray to be parallel to the incident ray (but laterally displaced), it must follow a path like Ray A. The other rays (B and C) show incorrect directions of bending during refraction at the air-glass interfaces.

Question 24: A ray of light strikes the surface of a rectangular glass block such that the angle of incidence in air is (i) 0°, (ii) 45°. In each case, draw diagram to show the path taken by the ray as it passes through the glass block and emerges from it. 

Ans: (i) Angle of Incidence = 0°

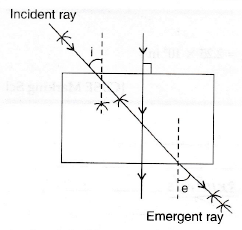
When the ray of light hits the glass block at a 0° angle (head-on, perpendicular to the surface), it passes straight through without bending. This is because the light is not entering at a slant, so there is no refraction. The ray will travel in a straight line through the glass, exit the opposite parallel face, and continue moving in its original direction. The path is a single straight line from air, through the glass, and back into the air.

(ii) Angle of Incidence = 45°

In this case, the ray will bend towards the normal as it enters the denser glass medium. Inside the block, it travels in a straight line until it reaches the opposite face. As it exits from glass back into the less dense air, it bends away from the normal. The final emergent ray is parallel to the original incident ray but is laterally displaced (shifted sideways). The path is a “Z”-shaped pattern consisting of the incident ray, an inward-bent ray inside the glass, and an outward-bent emergent ray.

Question 25: In the adjacent diagram, AO is a ray of light incident on a rectangular glass block. (a) complete the path of the ray till it emerges out of the block. (b) In the diagram, mark the angles of incidence (i) and the angle of refractive index of glass related to the angles 𝔦 and 𝔯 ? (c) mark angles of emergence by the letter ℯ. How are the angles I and e related? (d) which two rays are parallel to each other? Name them. (e) Indicate in the diagram the lateral displacement between the emergent ray and the incident ray. 

Ans: (a) Completing the Ray Path

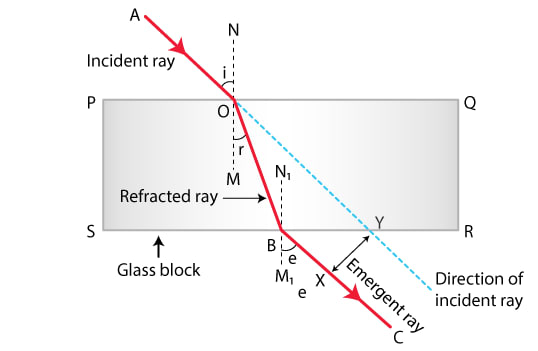
First, draw a normal (a dotted line perpendicular to the surface) at the point where ray AO hits the glass block. The ray will bend towards this normal as it enters the glass. Inside the glass, the ray travels in a straight line. At the far side of the block, draw another normal. The ray will bend away from this normal as it exits the block and returns into the air.

(b) Marking Angles and the Refractive Index

Angle of incidence (i): This is the angle between the incident ray (AO) and the normal at the first surface. Mark this angle inside the block and label it ‘i’.

Angle of refraction (r): This is the angle between the refracted ray inside the glass and the normal. Mark this angle inside the glass and label it ‘r’.

The refractive index of glass (n) is related to these angles by Snell’s Law: 

n=sini/sinr

(c) Angle of Emergence (e) and its Relation to (i)

Angle of emergence (e): This is the angle between the emergent ray (the ray leaving the block) and the normal at the second surface. Mark this angle outside the block and label it ‘e’.

The angle of incidence (i) and the angle of emergence (e) are equal for a rectangular glass slab with parallel sides. So, 

i=e.

(d) Identifying Parallel Rays

The two rays that are parallel to each other are the incident ray (AO) and the emergent ray (the final ray coming out of the block).

(e) Indicating Lateral Displacement

Lateral displacement is the perpendicular shift between the original path of the incident ray and the final path of the emergent ray. To show this, extend the incident ray (AO) in a straight dotted line in the same direction. Then, mark the perpendicular distance between this dotted line and the actual emergent ray. This gap is the lateral displacement.

Question 26: A ray of monochromatic green light enters a liquid from air, as shown in Fig 4.20. The angle 1 is 45° and angle 2 is 30°.   (a) Find the refractive index of liquid. (b) Show in the diagram the path of the ray after it strikes the mirror and re-enters in air. Mark in the diagram the angles where ever necessary. (c) Redraw the diagram if plane mirror becomes normal to the refracted ray inside the liquid. State the principal used. 

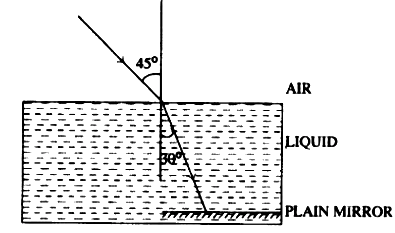
Ans: (a) Refractive index of liquid

Using Snell’s law:

n1sini=n2sinr

Here, 

n1=1(air), 

i=45 ∘ , r=30 ∘ .

n2=sin45∘

sin30∘=1/2​

 ≈1.414

So, refractive index of liquid = 1.414

(b) Path after striking mirror

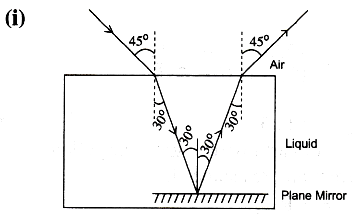
The refracted ray inside the liquid (at 30∘to normal) travels to the plane mirror placed at the bottom. By the law of reflection, the angle of incidence on the mirror equals the angle of reflection. After reflection, the ray travels upward, strikes the liquid-air interface at the same 30∘  on the other side, and emerges into air at 

45∘  (by reversibility of light path). The diagram should show:

At first air-liquid interface: incidence = 45∘, refraction = 30∘

At mirror: incidence = 60∘  with mirror surface (or 30∘  with normal), reflection = 30∘with normal

At second liquid-air interface: incidence = 30∘ , refraction = 45∘ into air.

(c) Redraw diagram if mirror is normal to refracted ray

If the plane mirror is placed normal to the refracted ray inside the liquid, the ray will hit the mirror at 0∘   incidence (along the normal), so it will reflect back on itself, retracing its path through the liquid and emerging into air at the original point of entry at 45∘.The principle used is: Angle of incidence = Angle of reflection for a plane mirror, and for normal incidence, the ray reverses its path.

Question 27: Light of a single colour is passed through a liquid having a piece of glass suspended in it. On changing the temperature of liquid, at a particular temperature the glass piece is not seen. (i) When is the glass piece not seen? (ii) Why is the light of a single colour used? 

Ans: (i) When is the glass piece not seen?

The glass piece becomes invisible when two specific conditions are met simultaneously:

The refractive index of the glass becomes exactly equal to the refractive index of the surrounding liquid.

The light used is monochromatic (a single colour).

When these conditions are satisfied, light rays pass from the liquid into the glass without undergoing any refraction (bending) or reflection at the interface between the two materials.

Here’s a simple analogy: Imagine a perfectly clear glass bead immersed in water. You can see it because light bends and reflects at its surface, creating a distinct boundary. Now, imagine if the bead were magically made of solid water with the same density and clarity as the surrounding water. It would be impossible to see because there would be no boundary for the light to interact with.

In this experiment, temperature is used as a control knob. Since the refractive index of a liquid changes more significantly with temperature than that of a solid (like glass), heating or cooling the liquid allows you to precisely tune its refractive index until it matches that of the suspended glass piece. At this precise temperature, the optical boundary vanishes, and the glass piece seems to disappear into the liquid.

(ii) Why is the light of a single colour used?

Light of a single colour (monochromatic light) is used for a crucial reason: to eliminate the effect of dispersion.

Dispersion is the phenomenon where different colours (wavelengths) of light bend by different amounts when passing through a material. This is what causes white light to split into a spectrum of colours in a prism.

If we used white light (which contains all colours) for this experiment, it would be nearly impossible to make the glass piece disappear completely. This is because the refractive index of both the glass and the liquid is slightly different for red light than it is for blue light. Even if you adjusted the temperature to match the refractive indices for one specific colour (say, green), the indices for other colours (red and blue) would still be mismatched. As a result:

Light of the matched colour (green) would pass through without deviation, making parts of the glass invisible.

Light of other colours (red and blue) would still refract and reflect at the boundaries.

The final effect would be a faint, coloured, ghost-like outline of the glass piece, instead of it completely disappearing. By using a single colour of light, we ensure that there is only one refractive index value to match for both materials, allowing for a perfect and complete disappearance of the glass piece at the specific temperature.

Question 28: When a lighted candle is held in front of a thick plane glass mirror, several images can be seen, but the second image is the brightest, give reason. 

Ans: When a candle flame is held in front of a thick plane glass mirror, multiple images are formed due to multiple reflections between the front and the back surface of the glass.

The first image is the dimmest. It is formed by reflection from the front surface of the glass (which has a silvered coating in a mirror). Only a small fraction of light (about 4-5%) is reflected here; most of the light enters the glass.

The second image is the brightest. It is formed by reflection from the silvered back surface of the mirror. The light travels through the glass, reflects from the silvered layer (which reflects most of the light), and then comes out. Since most of the light is used in forming this image, it is the brightest.

Subsequent images (third, fourth, etc.) are even dimmer because they are formed by light undergoing three or more reflections, losing intensity each time it reflects off a surface.

 Question 29: Fill in the blanks to complete the following sentences: 

(a) When light travels from a rarer to a denser medium, its speed. …………….. 

(b) When light travels from a denser to a rarer medium, its speed ………………. 

(c) The refractive index of glass with respect to air is 3/2. The refractive index of air with respect to glass will be ……………….  

Ans:  (a) When light travels from a rarer to a denser medium, its speed decreases 

(b) When light travels from a denser to a rarer medium, its speed increases 

(c) The refractive index of glass with respect to air is 3/2. The refractive index of air with respect to glass will be 2/3  

 MULTIPLE CHOICE TYPE: 

 Question 1: When a ray of light from air enters a denser medium, it: 

(a) bends away from the normal 

(b) bends towards the normal 

(c) goes undeviated 

(d) is reflected back 

Ans: The ray of light bends towards the normal. Reason: As the speed of light decreases in the denser medium, it bends towards the normal.    

Question 2: A light ray does not bend at the boundary in passing from one medium to the other medium if the angle of incident is: 

(a)  0°   

(b) 45°  

(c) 60°  

(d) 90°

Ans: (a)  0°   

Question 3: The highest refractive index is of: 

(a) Glass   

(b) Water        

(c) Diamond      

(d) Ruby Solution : Diamond 

Ans:(c) Diamond     .    

NUMERICALS:  

Question 1: The speed of light in air is 3 × 108 m s-1. Calculate the speed of light in glass. The refractive index of glass is 1.5 

Ans: We know that light slows down when it enters a material like glass from air. How much it slows down is determined by a property called the refractive index.

The formula that connects everything is:

Refractive Index (n) = (Speed of Light in Air) / (Speed of Light in the Medium)

Or, written more simply:

                                                  n = c / v

Where:

n is the refractive index of the material (glass, in our case).

c is the speed of light in air (or a vacuum).

v is the speed of light inside the medium (what we want to find).

Step 1: List out what we know.

From the problem, we are given:

Speed of light in air, c = 3 × 10⁸ m/s

Refractive index of glass, n = 1.5

Speed of light in glass, v = ? (This is our target)

Step 2: Rearrange the formula to solve for ‘v’.

We start with the original formula:

n = c / v

To find ‘v’, we need to get it by itself on one side. We can do this by swapping their positions:

v = c / n

This makes sense intuitively: the speed inside the glass is equal to the speed in air divided by the refractive index.

Step 3: Plug in the values.

Now we substitute the known numbers into our rearranged formula:

v = (3 × 10⁸ m/s) / 1.5

Step 4: Do the calculation.

Dividing 3 by 1.5 gives us 2.

So, v = 2 × 10⁸ m/s

Final Answer:

The speed of light in glass is 2 × 10⁸ metres per second.

Question 2: The speed of lllight in diamond is 125,000 km s-1. What is its refractive index? (speed of light in air = 3 × 108 m s-1). 

Ans: To determine the refractive index of diamond, we use the fundamental relationship that compares the speed of light in a vacuum, or air as a close approximation, to its speed within the material. The speed of light in air is a constant 300 million meters per second. The provided speed of light within diamond is 125,000 kilometers per second, which is first converted to 125 million meters per second to ensure consistent units. Dividing the speed in air by the speed in diamond (300 million divided by 125 million) yields a result of 2.4. This value is the refractive index, meaning light propagates 2.4 times slower in diamond than in air. It is this high refractive index that causes light to bend sharply and reflect extensively within the gem, creating its characteristic and dazzling sparkle.

Question 3: The refractive index of water with respect to air is 4/3. What is the refractive index of air with respect to water? 

Ans:The refractive index of air with respect to water is 3/4 or 0.75.

This is found by taking the reciprocal of the refractive index of water with respect to air (4/3).

Question 4:  A ray of light of wavelength 5400 Å suffer refraction from air to glass. Taking αμℊ = 3/2, find the wavelength of light in glass. 

Ans: 

When light travels from air to glass, its frequency remains constant, but the wavelength changes due to the change in speed. The refractive index 

μg=3/2  relates the wavelength in air (λa ) to the wavelength in glass (λg ) by the formula:

μg=λa/λg​

 Substituting the given values:

3/2=5400Å/λg

=5400×2/3

​ =3600Å

Thus, the wavelength of light in glass is 3600 Å.

EXERCISE – 4(B)  

Question 1: What is a prism? With the help of diagram of a prism, indicate its refracting surfaces, refracting edge and base.

Ans: A prism is a transparent optical element with flat, polished surfaces that can refract or disperse light. It is typically made of glass or plastic and has a triangular cross-section.

The main parts of a prism are:

Refracting Surfaces: These are the two polished, plane surfaces of the prism through which light enters and exits. These surfaces are inclined at an angle to each other and are responsible for bending the light.

Refracting Edge: This is the edge formed by the intersection of the two refracting surfaces. It is the apex of the triangular cross-section and acts as the primary line from which the angle of the prism is measured.

Base: This is the third surface of the prism, opposite to the refracting edge. It is generally not used for the passage of light and provides stability to the prism.

Although a diagram cannot be drawn here, one can be imagined as a triangle (like △ABC). In this triangle:

The two sides, AB and AC, represent the refracting surfaces.

The point A, where these two sides meet, is the refracting edge.

The side BC, opposite to point A, is the base of the prism.

When a ray of light passes through the prism, it bends towards the base of the prism after refraction.

Question 2: The diagrams (a) and (b) in Fig. 4.29 below show the refraction of a monochromatic ray of light through a parallel sided glass block and a prism respectively. In each diagram, label the incident, refracted emergent rays and the angle of deviation. 

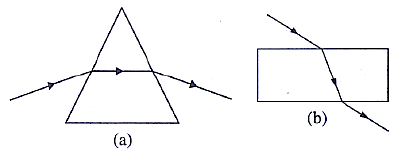
Ans:

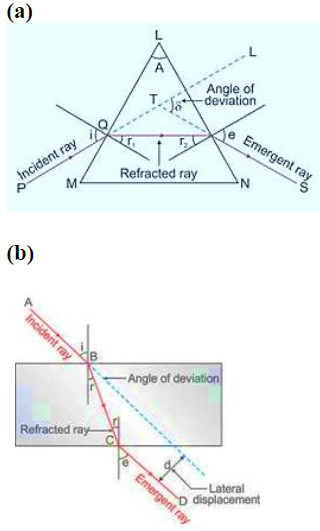
In diagram (a), the parallel-sided glass block:

The ray entering the glass block is the incident ray.

Inside the glass, the ray that bends towards the normal is the refracted ray.

The ray exiting the glass block is the emergent ray. Since the sides are parallel, the emergent ray is parallel to the incident ray.

The angle of deviation (δ) is the angle between the direction of the emergent ray and the original direction of the incident ray. In this case, the ray emerges parallel but is laterally displaced, so the angle of deviation is the small angle between these two parallel lines.

In diagram (b), the prism:

The ray approaching the first prism surface is the incident ray.

Inside the prism, the ray that bends towards the base is the refracted ray.

The ray leaving the second surface of the prism is the emergent ray.

The angle of deviation (δ) is the angle between the original path of the incident ray and the final path of the emergent ray. This angle is clearly visible as the prism causes a significant change in the ray’s direction.

Question 3: Define the term angle of deviation 

Ans: The angle of deviation is the angle between the original path of a light ray and its final path after it has been reflected or refracted by an optical device, such as a prism or a lens.

In simpler terms, when a ray of light enters a prism, it bends twice—once upon entering and once upon leaving. This double bending causes the emergent ray to travel in a different direction than the original incident ray. The angle of deviation measures how much the light ray has been “deviated” or turned from its initial course. This angle is not fixed; it depends on the angle of incidence and the material of the prism. A key concept in optics is the angle of minimum deviation, which is the smallest possible angle of deviation for a given prism and wavelength of light.

Question 4: Complete the following sentence: 

Angle of deviation is the angle which the …………………. Ray makes with the direction of ………………….. ray. 

Ans:  Angle of deviation is the angle which the emergent ray makes with the direction of the incident ray.

Question 5: What do you understand by the deviation produced by a prism? Why is it caused? State three factors on which the angle of deviation depends.

Ans:  The deviation produced by a prism is the angle between the incident ray entering the prism and the emergent ray leaving it. In simple terms, it measures how much the prism has bent the path of the light from its original direction. This bending is primarily caused by refraction. Inside the prism, when it exits through the second face, it speeds up again and bends away from the normal. These two refractions at the inclined surfaces cause the overall deviation of the light ray.

The three main factors on which the angle of deviation depends are:

The angle of the prism (A): A prism with a larger angle typically causes a greater deviation.

The material of the prism (Refractive Index): Different materials (like glass, plastic) have different refractive indices. A higher refractive index leads to a larger deviation.

The wavelength (or color) of light: Different colors of light bend by different amounts. For example, violet light deviates more than red light, which is why a prism creates a spectrum.

Question 6: How does the angle of deviation produced by a prism change with increase in the angle of incidence. Draw a curve showing the variation in the angle of deviation with the angle of incidence at a prism surface. 

Ans:

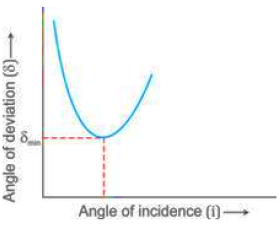
When light passes through a prism, the angle of deviation first decreases with an increase in the angle of incidence, reaches a minimum value, and then starts increasing again.

This variation can be shown on a graph plotting the angle of deviation (δ) against the angle of incidence (i). The resulting curve is a U-shaped parabola.

Initial Stage: As we increase the angle of incidence from a small value, the angle of deviation decreases.

Minimum Deviation: At a specific angle of incidence, the angle of deviation attains its minimum value (δm). At this point, the light ray passes symmetrically through the prism, meaning the angle of incidence is equal to the angle of emergence.

Final Stage: For angles of incidence beyond this point, the angle of deviation begins to increase again.

Therefore, the relationship is non-linear and the angle of deviation is minimum only for one particular angle of incidence.

The accompanying graph of angle of deviation (δ) versus angle of incidence (i) is a smooth curve, concave upwards, clearly showing this initial decrease and subsequent increase, with the bottom of the curve representing the point of minimum deviation.

Question 7: State whether the following statement is ‘true’ or ‘false’  The deviation produced by a prism is independent of the angle of incidence and is same for all the colours of light. 

Ans:  The statement is false.

Explanation:

The deviation produced by a prism depends on both the angle of incidence and the wavelength (colour) of light.

Dependence on angle of incidence:

For a given prism, the angle of deviation changes with the angle of incidence. It is minimum only at a particular angle of incidence (angle of minimum deviation).

Dependence on colour:

Different colours of light travel at different speeds in the prism material, causing dispersion. Hence, the refractive index varies with colour, leading to different deviations for different colours (violet deviates the most, red the least).

Thus, the statement is incorrect on both counts.

Question 8: How does the angle of minimum deviation produces by a prism change with increase in (i) the wavelength of incident light and (ii) the refracting angle of prism? 

Ans: (i) With an increase in the wavelength of incident light:

The angle of minimum deviation decreases as the wavelength of light increases. This happens because the refractive index of the prism material is higher for shorter wavelengths (like blue light) and lower for longer wavelengths (like red light). Since a higher refractive index causes light to bend more, shorter wavelengths experience a greater deviation. Therefore, as we move from violet to red light (increasing wavelength), the amount of bending decreases, leading to a smaller angle of minimum deviation.

(ii) With an increase in the refracting angle of the prism:

The angle of minimum deviation increases as the refracting angle of the prism increases. A prism with a larger refracting angle is physically sharper and has steeper sides. When light passes through such a prism, the overall bending of the light ray at both interfaces is more pronounced. This greater cumulative bending results in a larger angle of minimum deviation for the same material and wavelength of light.

Question 9 Write a relation for the angle of deviation (δ) for a ray of light passing through an equilateral prism in terms of the angle of incidence (i) angle of emergence (ℯ) and angle of prism(A). 

Ans:  The angle of deviation (δ) for a light ray passing through a prism is calculated using the formula δ = i + e – A. In this expression, ‘i’ represents the angle at which the light first strikes the prism, ‘e’ is the angle at which it finally exits, and ‘A’ is the prism’s own angle. Essentially, this relationship shows that the total bending of the light from its original path is a combined result of its entry and exit angles, minus the fixed geometry of the prism itself.

Question 10: A ray of light incident at an angle of incidence i1 passes through an equilateral glass prism such that the refracted ray inside the prism is parallel to its base and emerges at an angle of emergence i2. (i) How is the angle of emergence ‘i2’ related to the angle of incidence ‘i2’. (ii) what can you say about the angle of deviation in such a situation? 

Ans: (i) Relation between angle of emergence and angle of incidence

In this specific setup, since the refracted ray inside the prism is parallel to its base, the prism is in the position of minimum deviation. For minimum deviation in an equilateral prism, the passage of light is symmetric. This means the angle of incidence i1  is equal to the angle of emergence i2

Thus,

i2=i1

(ii) Angle of deviation in this situation

When the ray inside the prism is parallel to the base, the deviation suffered by the ray is the minimum deviation (δmin ).

At minimum deviation, the ray passes symmetrically through the prism, and the angle of deviation is the smallest possible for that prism and wavelength of light.

Question 11: How is the angle of emergence related to the angle of incidence when prism is in the position of minimum deviation? Illustrate your answer with help of a labelled diagram using an equilateral prism? 

Ans:

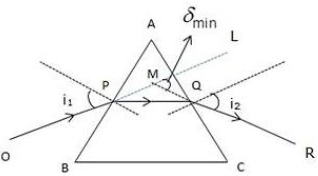
When a prism is in the position of minimum deviation, the ray of light passes symmetrically through the prism. This means:

If 

i is the angle of incidence and 

e is the angle of emergence, then at minimum deviation:

i=e

The refracted ray inside the prism becomes parallel to the base of the prism (in the case of an equilateral prism).

This symmetrical path occurs because the deviation of light is at its minimum value for a given prism and wavelength. Any other path where 

i≠e

i=e would result in a larger angle of deviation.

Illustration with a Labelled Diagram (Equilateral Prism)

The diagram below shows a ray of monochromatic light passing through an equilateral prism in the minimum deviation position.

Labelling:

Prism: Equilateral triangle ABC.

Incident Ray: The ray approaching face AB.

Angle of Incidence (i): The angle between the incident ray and the normal at point of incidence on face AB.

Refracted Ray: The ray inside the prism, shown parallel to the base BC.

Emergent Ray: The ray leaving face AC.

Angle of Emergence (e): The angle between the emergent ray and the normal at point of emergence on face AC.

As the prism is in the minimum deviation position, the two angles 

i and e are clearly equal.

Question 12: A light ray of yellow colour is incident on an equilateral glass prism at an angel of incidence equal to 48° and suffers minimum deviation by an angle of 36°. (i) What will be the angle of emergence? (ii) If the angle of incidence is changes to (a) 30°, (b) 60°, state whether the angle of deviation will be equal to, less than or more than 36° ?  

Ans: (i) Angle of Emergence

For a light ray undergoing minimum deviation in an equilateral prism, the ray inside the prism travels parallel to the base. In this symmetric path, the angle of incidence is equal to the angle of emergence. Since the angle of incidence is given as 48°, the angle of emergence will also be 48°.

(ii) Change in Angle of Incidence

The minimum deviation (36°) occurs only at a specific angle of incidence (48° in this case).

(a) If the angle of incidence is changed to 30°, the ray will no longer follow the path of minimum deviation. The angle of deviation will increase, meaning it will be more than 36°.

(b) If the angle of incidence is changed to 60°, this also deviates from the condition for minimum deviation. Similar to the previous case, the angle of deviation will again be more than 36°.

Question 13: Name the colour of white light which is deviated (i) the most, (ii) the least, on passing through a prism. 

Ans: (i) Violet colour is deviated the most.

(ii) Red colour is deviated the least.

When white light passes through a prism, it undergoes dispersion and splits into its constituent colours. Violet light has the shortest wavelength and bends the most, while red light has the longest wavelength and bends the least.

Question 14: Which of the two prism, A made of crown glass and B made of flint glass, deviates a ray of light more? 

Ans: Of the two, prism B made of flint glass deviates a ray of light more.

This happens because the ability of a material to bend light is determined by its refractive index.  When light enters a prism, this higher refractive index causes a greater change in the light’s speed and direction, resulting in a larger angle of deviation. Therefore, for the same angle of prism and under identical conditions, the flint glass prism will always bend the light ray more strongly.

Question 15: How does the angle of deviation depend on the refracting angle of the prism? 

Ans:  The angle of deviation in a prism depends directly on the refracting angle of the prism. For a given material and wavelength of light, a prism with a larger refracting angle will produce a larger angle of minimum deviation, and vice-versa

Question 16: An object is viewed through a glass prism with its vertex pointing upwards. It appears to be displaced upward. Explain the reason. [Hint: see solved example 1] 

Ans:

When viewed through a glass prism with its vertex pointing upwards, the object appears to be raised or displaced upward. This happens because of the refraction (bending) of light.

As the rays of light from the object travel from a denser medium (glass) into a rarer medium (air), they bend away from the normal. This bending occurs at the second surface of the prism. Since the prism’s vertex is upwards, this refraction causes the light rays to bend in a downward direction. Consequently, when these bent rays enter our eye, our brain traces them back in a straight line. This process makes the object appear to be coming from a point that is higher than its actual position, creating the illusion of an upward displacement.

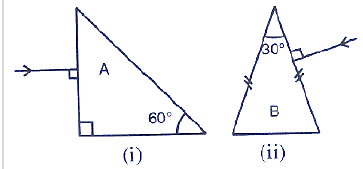
Question 17: A ray of light is normally incident on one face of an equilateral glass prism. Answer the following: (a) What is the angle of incidence on the first face of the prism? (b) What is the angle of refraction from the first face of the prism? (c) what will be the angle of incidence at the second face of the prism? (d) will the light ray suffer minimum deviation by the prism? 

Ans: (a) The light ray strikes the first face at a 0° angle of incidence because it is perpendicular to the surface.

(b) Since the angle of incidence is 0°, the ray enters the prism without bending, so the angle of refraction is also 0°.

(c) Inside the prism, the ray travels straight and meets the second face at an angle of incidence of 60°.

(d) Minimum deviation occurs when the path through the prism is symmetric. Here, the angles at the two faces are unequal (0° and 60°), so the ray does not undergo minimum deviation.

Question 18: Fig. 4.30 below shows two identical prisms A and B placed with their faces parallel to each other A ray of light of single colour PQ is incident at the face of the prism A. complete the diagram to show the path of the ray till it emerges out of the prism B.     [Hint: The e mergent ray out of the prism B will be parallel to the incident ray PQ]   

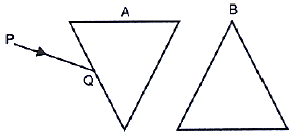
Ans:

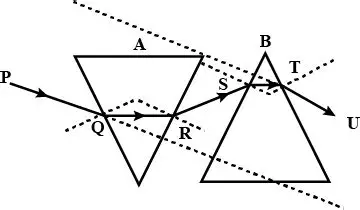
When a ray of light PQ enters prism A, it refracts (bends) towards the normal inside the prism and then bends away from the normal when emerging out, becoming parallel to its original direction but laterally displaced.

Since the two prisms A and B are identical and placed parallel to each other, the emergent ray from prism A will enter prism B at the same angle at which it emerged from A. Inside prism B, the ray again refracts similarly, and the final emergent ray from prism B will be exactly parallel to the initial incident ray PQ, following the principle of reversible path of light through identical mediums.

Question 19: Fig 4.31 below shows a light ray of single colour incident normally on two prisms A and B. In each case draw the path of the ray of light as it enters and emerges out of the prism. Mark the angle wherever necessary.  

Ans: The path of the light ray will be different for the two prisms because they are oriented differently relative to the incident ray.

For Prism A:

The light ray is incident normally (at a 90° angle) on the first surface. Since it is normal, it enters the prism without any bending and travels in a straight line to the opposite face. This opposite face is inclined. Here, the ray moves from a denser medium (glass) to a rarer medium (air) and will bend away from the normal. As it emerges, it will refract downwards, making an angle with its original direction. The angle between the emergent ray and the incident ray is the angle of deviation.

For Prism B:

In this orientation, the light ray is again incident normally on the first surface, so it enters without bending. It travels straight to the second surface, which is also parallel to the first. Because both surfaces are parallel, the ray emerges normally from the second surface as well. Therefore, the emergent ray is parallel to the incident ray but slightly displaced sideways. There is no net bending or deviation of the light ray in this case, as it passes through a glass slab with parallel sides.

Question 20: Complete Fig. 4.32 to show the path of the ray of single colour as it enters the prism and emerges out of it. Mark the angles wherever necessary.  

Ans:

When a ray of single colour enters a prism, it bends towards the normal at the first surface as it moves from air (rarer medium) to glass (denser medium). Inside the prism, it travels in a straight line until it reaches the second surface.

At the second surface, the ray bends away from the normal as it goes from glass to air. The path of the ray is thus deviated from its original direction. The angles of incidence and refraction at both faces should be marked, along with the angle of deviation between the incident and emergent rays.

MULTIPLE CHOICE TYPE:  

Question 1: In refraction of light through a prism, the light ray: 

(a) Suffers refraction only at one face of the prism.

 (b) emerges out from the prism in a direction parallel to the incident ray. 

(c) bends at both the surfaces of prism towards its base. 

(d) bends at both the surfaces of prism opposite to its base. 

Ans:  (c) bends at both the surfaces of prism towards its base. 

Question 2: A ray of light suffers refraction through an equilateral prism. The deviation produced by the prism does not depend on the: 

(a) angle of incidence

 (b) colour of light 

(c) material of prism 

(d) size of prism 

Ans: (d) size of prism 

NUMERICALS:  

Question 1: A ray of light incident at an angle 48° on a prism of refracting angle 60° suffers minimum deviation. Calculate the angle of minimum deviation. [Hint: δ min = 2𝔦 – A] 

Ans: For a prism, when a ray of light undergoes minimum deviation, it passes symmetrically through the prism. This means the angle of incidence is equal to the angle of emergence.

The provided formula for this condition is:

δ_min = 2i – A

Where:

δ_min is the angle of minimum deviation.

i is the angle of incidence (which equals the angle of emergence).

A is the refracting angle of the prism.

Given:

Angle of incidence, i = 48°

Refracting angle, A = 60°

Substituting the given values into the formula:

δ_min = (2 × 48°) – 60°

δ_min = 96° – 60°

δ_min = 36°

Therefore, the angle of minimum deviation is 36°.

EXERCISE – 4 (C) 

 Question 1: How is the refractive index of a medium related to the real and apparent depths of an object in that medium? 

Ans:  The refractive index of a medium is directly related to the real and apparent depths through a simple ratio. When an object is placed inside a denser medium, like water, and viewed from above, it appears to be at a shallower depth than it actually is. This perceived depth is called the apparent depth, while the actual distance to the object is the real depth. The refractive index (n) of the medium is given by the formula: n = Real Depth / Apparent Depth. Therefore, a higher refractive index means a greater difference between the real and apparent depths, making the object appear much closer to the surface.

 Question 2: Prove that Refractive index = 𝑅𝑒𝑎𝑙 𝑑𝑒𝑝𝑡ℎ /𝐴𝑝𝑝𝑎𝑟𝑒𝑛𝑡 𝑑𝑒𝑝𝑡ℎ 

Ans:

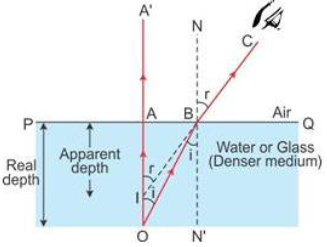
When an object rests at the bottom of a denser medium like water, it looks raised from its true position. This happens because light rays from the object bend away from the normal as they move from water into the air.

The actual distance from the surface to the object is the real depth, while the seemingly shorter distance we perceive is the apparent depth. For small viewing angles, Snell’s law simplifies this relationship. The refractive index of the denser medium is then equal to the real depth divided by the apparent depth, proving that the object appears shallower than it truly is.

Question 3: A tank of water is viewed normally from above. State how does the depth of tank appear to change. Draw a labelled ray diagram to explain your answer. 

Ans: When viewed normally from above, the depth of a water tank appears less than its actual depth.

Explanation:

This happens due to the refraction of light. Light rays coming from the bottom of the tank bend away from the normal as they pass from water (a denser medium) into air (a rarer medium). Our brain, however, interprets these rays as if they have traveled in a straight line. This causes the virtual image of the bottom to be formed at a shallower depth, making the entire tank of water appear shallower.

Labelled Ray Diagram:

The ray diagram would show:

A Water Tank: with a marked Actual Depth.

An Observer’s Eye above the water surface.

Two rays originating from a point at the bottom of the tank.

Refraction: The rays bending away from the normal as they cross the air-water boundary.

Virtual Image: The refracted rays, when traced backwards (shown as dotted lines), meet at a point higher up, creating a Virtual Image of the bottom.

Apparent Depth: The distance from the surface to this virtual image is labelled as Apparent Depth, which is clearly less than the Actual Depth.

In essence, the tank looks shallower because we see a raised, virtual image of its bottom.

 Question 4: Water in a pond appears to be only three – quarters of its actual depth. What property of light is responsible for this observation? Illustrate your answer with the help of a ray diagram. How is the refractive index of water calculated from its real and apparent depth? 

Ans: The property of light responsible for the pond appearing shallower than it really is is refraction. Refraction is the bending of light rays when they pass from one transparent medium (like water) into another (like air).

This happens because light rays traveling upwards from the object in the water bend away from the normal as they enter the less dense air. Our brain, however, assumes that light travels in a straight line. Therefore, when we see the bent rays, we perceive them as having come from a point higher up, making the bottom of the pond look closer than it actually is. This apparent, raised image is what we call the apparent depth.

Ray Diagram:

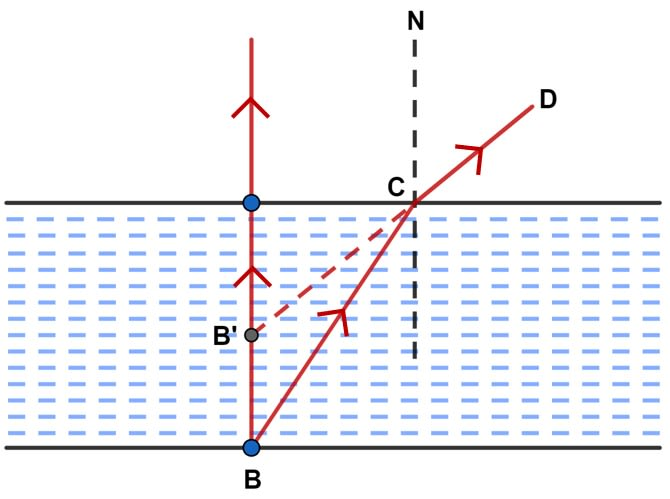
Draw a water-air interface (a horizontal line).

Mark a point ‘O’ at the bottom of the water (real depth).

Draw two rays from ‘O’ moving upwards. As they cross the interface into the air, bend them away from the normal (the vertical line).

Extend these refracted rays backwards (with dashed lines) into the water. They will meet at a point ‘I’ above ‘O’.

This point ‘I’ is the apparent position of the object, and the distance to it from the surface is the apparent depth.

Calculating Refractive Index:

The refractive index of water can be calculated directly from this observation using the relationship between real and apparent depth.

The formula is:

Refractive Index of Water (μ) = Real Depth / Apparent Depth

In this specific case, the apparent depth is three-quarters of the real depth. So, if the real depth is ‘d’, then the apparent depth is ‘(3/4)d’.

μ = d / (3d/4) = 4/3 ≈ 1.33

Thus, the refractive index of water is calculated to be approximately 1.33.

Question 5: Draw a ray diagram to show the appearance of a stick partially immersed in water explain your answer. 

Ans:  

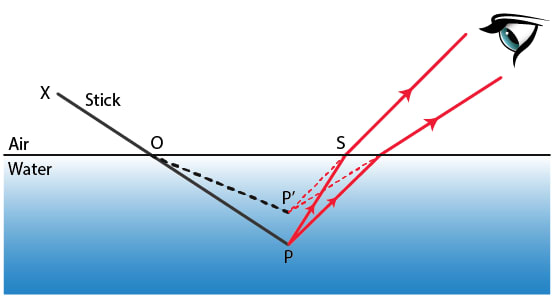
When a stick is partially immersed in water, it appears to be bent or broken at the water surface. This happens because light rays coming from the submerged part of the stick bend when they pass from water into air.

Water is optically denser than air. When light rays travel from the water into the air, they bend away from the normal line. Our eyes, however, always perceive light as traveling in a straight line. Therefore, our brain traces the bent rays coming from the stick backwards in a straight line. This makes the submerged part of the stick seem to be at a higher position than it actually is. The result is that the stick looks bent upwards at the point where it enters the water.

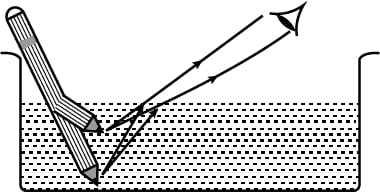
Question 6: A student puts his pencil into an empty trough and observes the pencil from the position as indicated in Fig.

Ans:

Based on the described situation, when a student places a pencil in an empty trough and views it from the side, the pencil appears bent or broken at the surface.

This happens because light from the submerged part of the pencil travels from water to air. As light moves into the less dense air, it bends away from the normal line. Our brain, however, assumes that light travels in a straight line. This causes the submerged section of the pencil to appear at a different position, making the pencil look bent where the air and water meet.

Question 7: A fish is looking at a 1.0m high plant at the edge of the pond. Will the plant appear shorter or taller than its actual height, to the fish. Draw a ray diagram to support your answer. 

Ans: This happens because the fish is underwater and views the plant through the refracting surface of water. When light from the top of the plant travels from air into water, it bends towards the normal as it enters the water. As a result, the rays seem to come from a point higher than the actual position of the top of the plant. Similarly, rays from the bottom of the plant (near the water surface) undergo less deviation. This makes the plant appear extended vertically, so the fish sees it as taller.

Ray Diagram Concept:

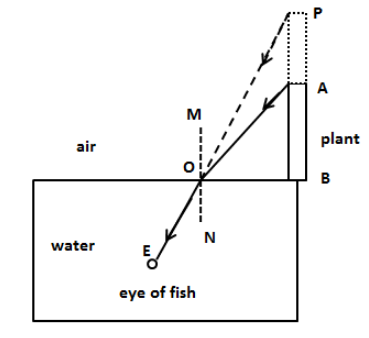
Draw water surface as a horizontal line.

Mark the plant above the surface (in air).

From the top of the plant, draw rays going downward toward the water surface and bending toward the normal as they enter the water.

Extend these refracted rays backward (virtual rays) to form a virtual image of the plant that is taller.

The fish’s eye in water sees this virtual image.

Question 8: An object placed in one medium when seen from the other medium, appears to be vertically shifted. Name two factors on which the magnitude of shift depends and state how does it depend on them.

Ans:   The apparent vertical shift of an object seen through different media is determined by two main factors. First, the shift increases with the thickness of the medium between the object and the observer; a thicker layer causes a greater displacement. Second, the shift depends on the refractive indices of the two media involved. It is directly related to the ratio (μ₂/μ₁ – 1), where μ₁ is the refractive index of the object’s medium and μ₂ is that of the observer’s medium. A larger difference between these indices leads to a more significant apparent shift in the object’s position.

 MULTIPLE CHOICE TYPE:  

Question 1: A small air bubble in a glass block when seen from above appears to be raised because of: 

(a) refraction of light  

(b) reflection of light  

(c) reflection and refraction of light (d) none of the above 

Ans: (a) refraction of light  

 Question 2: An object in a denser medium when viewed from a rarer medium appears to be raised. The shift is maximum for: 

(a) red light 

(b) violet light 

(c) yellow lighten  

(d) green light 

Ans:  (b) violet light 

NUMERICALS:

Question 1: A Water pond appears to be 2.7 m deep. If the refractive index of water is 4/3, find the actual depth of the pond. 

Ans: The apparent depth of the pond is observed to be 2.7 m, and the refractive index of water is given as 4/3

The relationship between the real depth, apparent depth, and refractive index is expressed as:

μ=Real Depth/Apparent Depth

Substituting the known values into the equation:

4/3=Real Depth/2.7

To find the real depth, we rearrange the formula:

Real Depth=4/3×2.7

Calculating the result:

Real Depth=4/3×27/10

=108/30

=3.6 m

Therefore, the actual depth of the pond is 3.6 meters.

Question 2: A coin is places at the bottom of a beaker containing water (refractive index = 4/3) to a depth of 12 cm. By what height the coin appears to be raised when seen from vertically above?  

Ans: When an object is placed underwater and viewed from directly above, the light rays coming from it bend as they pass from the water into the air. This bending of light, known as refraction, causes the object to appear at a different position than where it actually is. Specifically, an object underwater appears closer to the surface than it really is.

In this scenario, we are told that a coin is placed at a real depth of 12 cm below the water’s surface. The refractive index of water is given as 4/3.

The relationship between the real depth and the apparent depth is governed by a simple formula:

Apparent Depth = Real Depth / Refractive Index

Plugging in the given values:

Apparent Depth = 12 cm / (4/3)

Dividing by a fraction is the same as multiplying by its reciprocal, so:

Apparent Depth = 12 cm × (3/4) = 9 cm

This means that to an observer looking straight down, the coin seems to be only 9 cm below the water’s surface.

To find out by how much the coin appears to be raised, we subtract the apparent depth from the real depth:

Height Raised = Real Depth – Apparent Depth

Height Raised = 12 cm – 9 cm = 3 cm

Therefore, due to the refraction of light, the coin appears to be raised by 3 cm from its actual position.

Question 3: A postage stamp kept below a rectangular glass block of refractive index 1.5 when viewed from vertically above it, appears to be raised by 7.0 mm. calculate the thickness of the glass block. 

Ans: We use the apparent depth formula:

Real depth−Apparent depth=7.0 mm

Let real depth =t.

Apparent depth 

=t/μ

=t/1.5

So,

t−t/1.5=7.0

t(1−1/1.5)=7.0

t(1−2/3)=7.0

t×1/3=7.0

t=21.0 mm

Final answer: 21.0 mm

​

EXERCISE – 4 (D) 

 Question 1: Explain the term critical angle with the aid of a labelled diagram. 

Ans:

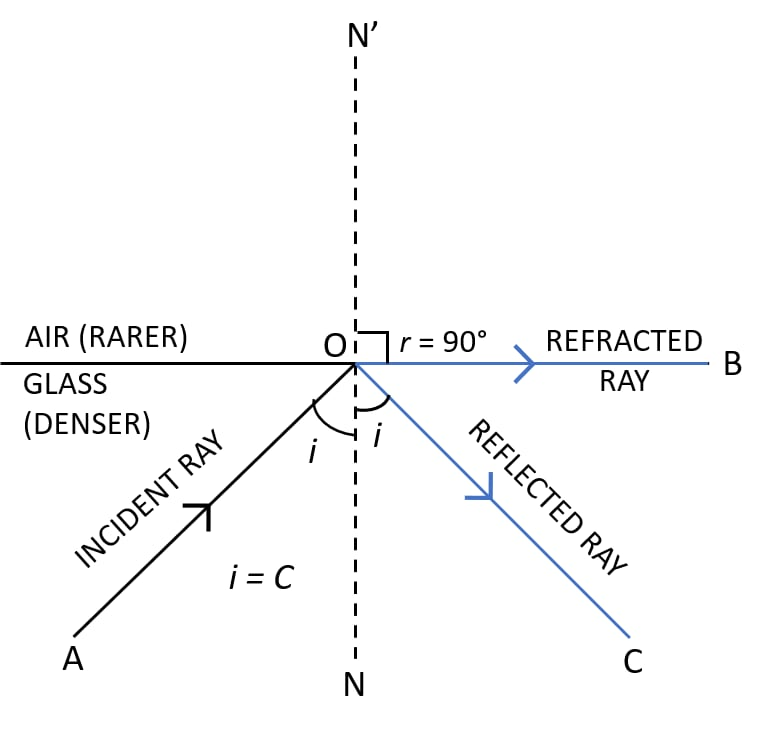
When light travels from a denser medium into a rarer medium, it bends away from the normal. The critical angle is the specific angle of incidence in the denser medium for which the angle of refraction in the rarer medium is exactly 90 degrees.

This can be understood with a labelled diagram. Imagine a light ray inside a glass slab (denser medium) heading towards its boundary with air (rarer medium). As you increase the angle of incidence (∠i), the refracted ray in the air bends further away from the normal. At one particular value of ∠i, the refracted ray just grazes along the surface, making a 90-degree angle with the normal. This specific angle of incidence is the critical angle.

If the angle of incidence is increased beyond this critical value, the light ray does not exit the denser medium at all. Instead, it reflects completely back into the same medium, a phenomenon known as Total Internal Reflection.

Question 2: How is the critical angle related to the refractive index of a medium? Solution 2: The critical angle is related to the refractive index of a medium by the relation μ= 1 sin𝑖𝑐  = cosecic    

Ans:The critical angle and the refractive index of a medium are inversely related. The formula that connects them is μ = 1 / sin i c, where ‘μ’ is the refractive index and ‘i c’ is the critical angle. This means that for a material with a very high refractive index, the critical angle will be relatively small. Conversely, a lower refractive index results in a larger critical angle. In essence, the refractive index determines the specific angle at which total internal reflection will begin to occur.

Question 3: State the approximate value of the critical angle for (a) glass-air surface (b) water-air surface. 

Ans:At a glass-air boundary, the critical angle is roughly 42°, whereas for water-air, it is a larger 49°. This variation arises because glass possesses a higher refractive index than water. A higher index causes light to bend more significantly towards the normal. Consequently, a smaller angle of incidence inside the material is sufficient to achieve a 90° refracted angle, leading to the smaller critical angle observed in glass.

 Question 4: What is meant by the statement the critical angle for diamond is 24°? 

Ans:The critical angle for diamond is the specific angle of incidence within the diamond at which light, traveling from diamond to air, is refracted at an angle of 90 degrees along the boundary. A critical angle of 24° means that if a light ray inside the diamond strikes the surface at an angle greater than this 24-degree limit, it will not escape into the air but will undergo total internal reflection instead. This very small critical angle is a result of diamond’s exceptionally high refractive index, which is why diamonds sparkle so brilliantly, as light entering them is easily trapped and reflected multiple times inside before eventually exiting.

Question 5: A light ray is incident from a denser medium on the boundary separating it from a rarer medium at an angle of incident equal to the critical angle, what is the angle of refraction for the ray? 

Ans:

When a light ray travels from a denser medium towards a rarer medium at the critical angle, the angle of refraction is 90 degrees. This means the refracted ray does not enter the rarer medium but instead travels exactly along the boundary between the two media.

Question 6: Name two factors which affect the critical angle for a given pair of media. State how do the factors affect it. 

Ans:Two factors affecting the critical angle are:

1. The Refractive Indices of the Two Media

The critical angle depends on the pair of media in contact. Specifically, it is determined by the ratio of their refractive indices. The critical angle (c) is given by sin c = n₂/n₁, where n₁ is the refractive index of the denser medium and n₂ is the refractive index of the rarer medium. If the difference between their refractive indices increases (meaning n₁ becomes larger relative to n₂), the ratio n₂/n₁ decreases, which causes the critical angle to become smaller. Conversely, a smaller difference leads to a larger critical angle.

2. The Wavelength (or Colour) of Light

The critical angle also depends on the wavelength of light used. A medium’s refractive index is slightly different for different wavelengths of light due to dispersion. For shorter wavelengths, like blue light, the refractive index is higher than for longer wavelengths, like red light. Therefore, for the same pair of media, blue light has a slightly smaller critical angle than red light because the higher refractive index leads to a smaller n₂/n₁ ratio.

Question 7: The critical angle for glass-air is 45° for the light of yellow colour. State whether it will be less than, equal to, or more than 45° for (i) ref light, (ii) blue light? 

Ans: The critical angle is the specific angle inside a material at which light trying to exit into the air bends so much that it skims along the surface. Any angle larger than this, and the light reflects entirely back inside, a phenomenon called total internal reflection.

This critical angle is determined by the material’s refractive index. A higher refractive index means light travels more slowly in the material and bends more sharply when exiting, which leads to a smaller critical angle.

(i) For Red Light:

Red light has the longest wavelength in the visible spectrum. Because of this, it interacts slightly less with the atoms of the glass, allowing it to travel a bit faster compared to other colours. This results in a slightly lower refractive index for red light in glass.

Since the refractive index is lower for red light, the light doesn’t bend as sharply. It can therefore escape the glass at a wider range of angles. Consequently, the critical angle for red light will be larger than 45°.

(ii) For Blue Light:

Blue light has a much shorter wavelength than yellow light. This shorter wavelength causes it to interact more strongly with the glass, slowing it down more effectively. This results in a slightly higher refractive index for blue light.

With a higher refractive index, blue light bends more sharply when it tries to exit. It reaches the “skim-the-surface” condition at a shallower angle inside the glass. Therefore, the critical angle for blue light will be smaller than 45°.

In summary, you can think of it as:

Lower refractive index → Larger critical angle (Red Light)

Higher refractive index → Smaller critical angle (Blue Light)

Question 8: (a) What is total internal reflection? (b) State two conditions necessary for total internal reflection to occur. (c) Draw diagram to illustrate the total internal reflection  

Ans:(a) What is total internal reflection?

Total internal reflection is an optical phenomenon where a ray of light, traveling from a denser medium into a less dense medium (like from glass to air), is completely reflected back into the denser medium. Instead of passing through and bending away from the normal (refracting), it reflects off the boundary as if it had hit a perfect mirror.

(b) Two conditions necessary for total internal reflection to occur.

The two essential conditions for total internal reflection are:

The light must be traveling from a denser medium towards a less dense medium (for example, from water to air or from glass to water).

The angle at which the light ray strikes the boundary (known as the angle of incidence) must be greater than a specific critical angle for that pair of materials.

(c) Diagram to illustrate total internal reflection.

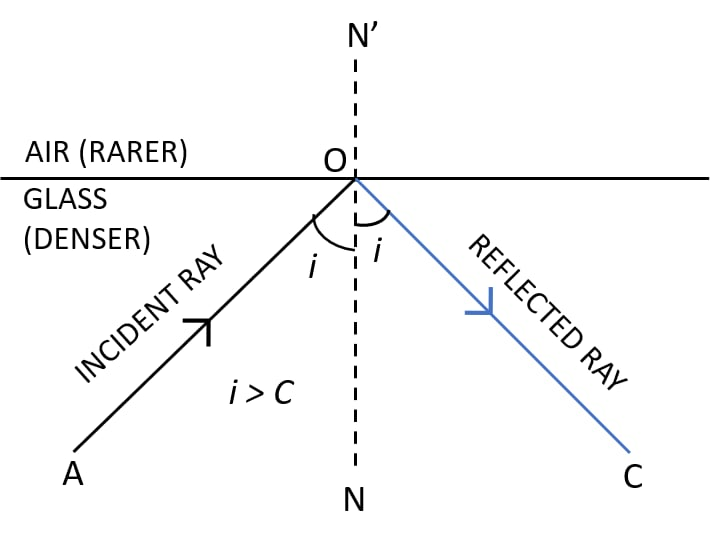
The diagram below shows a ray of light traveling inside a glass block towards an air boundary.

A light ray approaches the boundary. At a small angle of incidence, it refracts (bends away from the normal) and a weak reflected ray is also seen.

As the angle of incidence increases, the refracted ray bends further until it just skims along the boundary. This specific angle is the critical angle.

When the angle of incidence is increased beyond this critical angle, total internal reflection occurs. The light ray is now completely reflected back inside the glass, following the law of reflection.

Question 9: Fill in the blanks to complete the following sentence:

 (a) Total internal reflection occurs only when a ray of light passes from a …………….. medium to a ………………. Medium. 

(b) critical angle is the angle of …………….  In denser medium for which the angle of ………….. in rarer medium is…………………. 

Ans: (a) Total internal reflection occurs when a ray of light passes from a denser medium to a rarer medium. 

(b) Critical angle is the angle of incidence in denser medium for which the angle of refraction in the rarer medium is 90°.   

 Question 10: State whether the following statement is true or false: If the angle of incidence is greater than the critical angle, light is not refracted at all, when it falls on the surface from a denser medium to a rarer medium. 

Ans: True.    

Question 11: The refractive index of air with respect to glass is expressed as g μ a = 𝑆𝑖𝑛 𝑖 sin𝑟 . (a) Write down a similar expression for a μ g in terms of the angles i and r. (b) if angle r = 90°, what is the corresponding angle i called?  (c) what is the physical significance of the angle i in part (b)? 

Ans:(a) The expression for 

aμg (refractive index of glass with respect to air) in terms of angles i and r is:

aμg=sini/sinr

This is the reciprocal of the given expression gμa

(b) If the angle r=90 ∘ , the corresponding angle i is called the critical angle.

(c) The physical significance of this critical angle is that it represents the minimum angle of incidence in the denser medium (glass) for which total internal reflection occurs when light travels from glass to air. For any angle of incidence greater than the critical angle, the light is completely reflected back into the denser medium.

Question 12: The given figure shows a point source P inside a water container three rays A,B and C starting from the source P are shown up to the water surface. (a) show in the diagram the path of these rays after striking the water. The critical angle for water-air surface is 48°. (b) Name the phenomenon which the rays A, B and C exhibit.  

Ans:

(a) In the diagram:

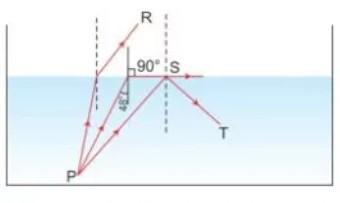
Ray A, incident at an angle less than the critical angle (48°), will refract away from the normal as it enters the air.

Ray B, incident exactly at the critical angle (48°), will travel along the water-air surface (grazing emergence).

Ray C, incident at an angle greater than the critical angle, will undergo total internal reflection and reflect back into the water following the laws of reflection.

(b) The phenomenon exhibited by the rays is total internal reflection (for Ray C) and refraction (for Rays A and B).

Question 13: In the given figure PQ and PR are the two light rays emerging from an object P. The ray PQ is refracted as QS. 

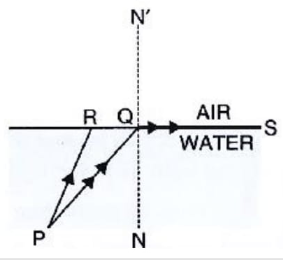
(a) state the special name given to the angle of incidence ∠PQN of the ray PQ.

(b) what is the angle of refraction for the refracted ray QS?

(c) name the phenomenon that occurs if the angle of incidence ∠ PQN is increased.

(d) The ray PR suffers partial reflection and refraction on the water-air surface. Give reason. Draw in the diagram the refracted ray for the incident ray PR and hence show the position of image of the object P by the letter P’ when seen vertically from above. 

Ans:(a) The special name given to the angle of incidence ∠PQN is the critical angle. This is the specific angle of incidence in the denser medium for which the angle of refraction in the rarer medium is 90 degrees.

(b) For the refracted ray QS, which is grazing along the water-air surface, the angle of refraction is 90 degrees.

(c) If the angle of incidence ∠PQN is increased beyond the critical angle, the phenomenon of total internal reflection occurs. In this case, no light refracts into the air; instead, all of it is reflected back into the water.

(d) The ray PR suffers partial reflection and refraction because its angle of incidence is less than the critical angle. When a light ray strikes a boundary at an angle smaller than the critical angle, it splits into two parts: a refracted ray that bends away from the normal in the air and a weaker reflected ray that stays in the water. To find the image position P’, the refracted ray for PR is extended backwards into the water (as shown by the dotted line in the diagram). The point where this backward extension meets the vertical line from P gives the location of the virtual image P’. This image P’ will appear higher than the actual object P when viewed from above.

Question 14: The refractive index of glass os 1.5. From a point P inside a glass block, draw rays PA, PB and PC incident on the glass air surface at an angle of incidence 30°, 42° and 60° respectively. (a) In the diagram show the approximate direction of these rays as they emerge out of the block. (b) What is the angle of refraction for the ray PB? (Take sin 42° = 2 3)

Ans:(a) Ray directions after emerging from the block:

Ray PA (30° incidence):

This ray will emerge into the air because 30° is less than the critical angle. It will bend away from the normal.

Ray PB (42° incidence):

The critical angle c of glass is given by

sinc=1/1.5=2/3≈0.6667

Since 

sin42∘=2/3 , the angle of incidence here equals the critical angle. So PB will emerge grazing along the glass-air surface (angle of refraction = 90°).

Ray PC (60° incidence):

60° is greater than the critical angle (~42°), so total internal reflection occurs. This ray will not emerge into air; it will reflect back into the glass following the laws of reflection.

(b) Angle of refraction for ray PB:

Since PB is incident at the critical angle, the angle of refraction in air is 90∘

Question 15: A ray of light enters a glass slab ABDC as shown in fig. 4.59 and strikes at the centre O of the circular part AC of the slab. The critical angle of glass is 42°. Complete the path of the ray till it emerges out from the slab. Mark the angles in the diagram wherever necessary. 

Ans:

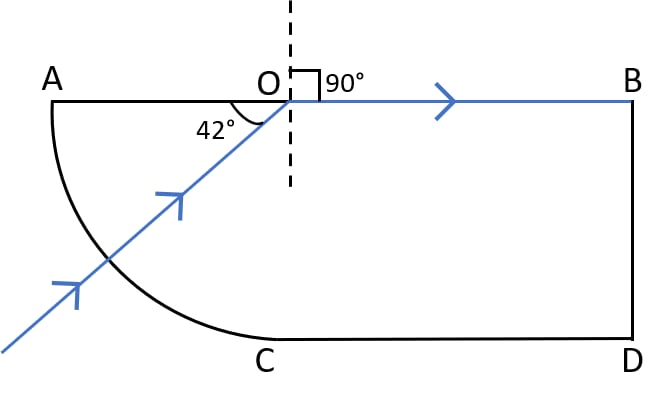
The ray strikes the circular surface AC normally at O, so it passes undeviated into the glass and hits the bottom surface BD at an angle of 45°.

The critical angle is 42°, so total internal reflection (TIR) occurs at BD because 45° > 42°.

The ray reflects upward at 45° and meets the circular surface AC again. At this point, it strikes at 45° to the normal. Since 45° is greater than the critical angle, TIR occurs again.

After this second TIR, the ray travels downward and meets the bottom surface BD at normal incidence (0°), so it emerges without bending.

Thus, the path includes two total internal reflections inside the glass slab before final emergence.

Question 16: What is a total reflecting prism? State three actions that it can produce. Draw a diagram to show one action of the total reflecting prism. 

Ans:

A total reflecting prism is a right-angled prism made of optical glass, designed to use the principle of total internal reflection. For this to occur, a light ray must strike the inner surface at an angle greater than the critical angle of the glass-air boundary (typically 42° for crown glass).

Three actions it can produce are:

Deviating a Light Ray by 90°: A ray entering one face perpendicularly strikes the hypotenuse face at an angle of 45° (greater than the critical angle). It is totally reflected, causing the ray to turn 90 degrees from its original path.

Inverting an Image (Erecting Prism): Used in instruments like binoculars, two such prisms are arranged to invert and revert an image, making the final image erect for the viewer.

Deviating a Light Ray by 180°: A ray entering the prism is totally reflected twice from the two perpendicular faces. This reverses the direction of the ray, sending it back parallel to its original path.

Explanation of the Diagram:

A light ray enters the prism perpendicular to one of the shorter faces. It travels in a straight line and strikes the hypotenuse (the slanted face) at a 45° angle. Since this angle is greater than the critical angle, the ray undergoes total internal reflection. It is then reflected at 90°, exiting through the other shorter face. This action is commonly used in periscopes.

Question 17: Show with the help of a diagram how a total reflecting prism can be used to turn a ray of light through 90°. Name one instrument in which such a prism is used. 

Ans:

A total reflecting prism is used to deviate a light ray by 90° using the principle of total internal reflection.

The prism is shaped as a right-angled isosceles prism (with angles 45°, 90°, and 45°). The ray of light is directed to strike one of the perpendicular faces at a 90° angle, so it enters the prism without bending. This ray then travels inside and falls on the hypotenuse face at an angle of 45°.

Since the critical angle for glass is about 42°, this 45° angle of incidence is greater than the critical angle. Therefore, the ray undergoes total internal reflection at the hypotenuse face. After reflection, the ray turns through 90° and emerges from the other perpendicular face of the prism.

Diagram Description:

A right-angled isosceles prism is shown. An incident ray enters through one perpendicular face, hits the hypotenuse at 45°, reflects totally, and emerges from the adjacent perpendicular face, having turned 90° from its original path.

One common instrument that uses such a prism is a periscope.

Question 18: A ray of light OP passes through a right angles prism as shown in the adjacent diagram. (a) State the angles of incidence at the faces AC and BC. (b) Name the phenomenon which the ray suffers at the face AC. 

Ans:

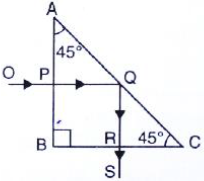
(a) At face AC, the angle of incidence is 45°.

At face BC, the angle of incidence is 0° (since the ray falls normally on BC).

(b) At face AC, the ray undergoes total internal reflection.

This happens because the angle of incidence (45°) is greater than the critical angle of the prism material, causing the light to be completely reflected back inside the prism instead of refracting out.

Question 19: In fig. 4.61, a ray of light PA is incident normally on the hypotenuse of an isoceles right angle prism ABC. (a) Complete the path of the ray PQ till it emerges from the prism. Mark in the diagram the angle wherever necessary. (b) what is the angle of deviation of the ray PQ? (c) Name a device in which this action is used. 

Ans:(a)The ray PA is incident normally on the hypotenuse AC, so it enters the prism undeviated along AB. Inside the prism, it strikes the face BC at an angle of incidence of 45°. Since the prism is isosceles right-angled (angles 90°, 45°, 45°) and made of glass (refractive index ~1.5), the critical angle is about 42°.

Thus, at face BC, the angle of incidence (45°) is greater than the critical angle, so total internal reflection occurs. The ray then travels to face AC, again striking it at 45° (greater than critical angle), and is totally internally reflected again, finally emerging normally from the hypotenuse AC along the direction opposite to the incident ray but parallel to the original path.

(b)After two total internal reflections, the emergent ray is parallel to the incident ray but in the opposite direction. The angle of deviation is 180°.

(c)This action of a light ray undergoing two total internal reflections to turn back exactly 180° is used in a periscope or a prism binoculars (specifically a Porro prism).

Question 20: What device other than a plane mirror can be used to turn a ray of light through 180°? Draw a diagram in support of your answer. Name an instrument in which this device is used. 

Ans:

A concave mirror can turn a ray of light through 180°, sending it directly back along its original path. This happens when a light ray is directed along the principal axis towards the mirror’s pole; it reflects back on itself, achieving a complete 180° turn.

This principle is used in an Astronomical Telescope. In the Cassegrain design of such a telescope, a large concave primary mirror collects light from distant celestial objects and reflects it to a smaller convex secondary mirror. This secondary mirror then reflects the light beam back through a hole in the primary mirror, effectively turning the light path around to reach the eyepiece.

 Question 21: Mention one difference between reflection of light from a plane mirror and total internal reflection of light from a prism. 

Ans: In reflection from a plane mirror, a portion of the incident light is always absorbed by the mirror’s surface. However, in total internal reflection from a prism, no light is absorbed or refracted; the entire incident light beam is completely reflected back into the denser medium.

 Question 22: State one advantage of using a total reflecting prism as a reflector in place of plane mirror. 

Ans:A key advantage of a total reflecting prism over a plane mirror is that it provides a much brighter and sharper reflection. This is because a prism reflects 100% of the incident light through total internal reflection, whereas a plane mirror’s silvered surface always absorbs a small amount of light, leading to a dimmer image.

Question 23: In given figure a ray of light PQ is incident normally on the face AB of an equilateral glass prism. Complete the ray diagram showing its emergence into air after passing through the prism. (a) Write the angles of incidence at the faces AB and AC of the prism. (b) name the phenomenon which the ray of light suffers at the face AB, AC and BC of the prism. 

Ans:

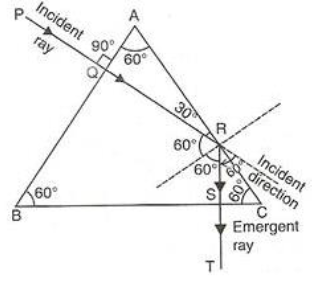
(a) The ray PQ is incident normally on face AB. Therefore, the angle of incidence at face AB is 0°. For face AC, the ray inside the prism strikes it at an angle of incidence of 30°.

(b)At face AB: Refraction (without deviation, as incidence is normal).

At face AC: The ray undergoes Refraction again, bending away from the normal as it enters the air.

At face BC: Total Internal Reflection occurs here, as the incident ray strikes the glass-air interface at an angle greater than the critical angle, causing it to reflect entirely back inside the prism.

Question 24: Draw a neat labelled ray diagram to show the total internal reflection of a ray of light normally incident on one face of a 30°, 90°, 60° prism. 

Ans:A neat labelled ray diagram for total internal reflection in a 30°, 90°, 60° prism is described below.

Ray Diagram Description:

Prism Orientation: Draw the prism with the 90° angle at the top and the 30° and 60° angles at the base. The face opposite the 90° angle (the longest side) is the base.

Incident Ray: Draw a ray of light approaching the first face of the prism and striking it at a perfect 90-degree angle (normal incidence). Since it is normal to the surface, this ray will travel straight into the prism without any bending.

Internal Incidence: Inside the prism, this ray will travel straight and strike the hypotenuse (the prism’s longest face) at an angle of 45°. This is the key internal surface.

Total Internal Reflection: For a glass prism, the critical angle is about 42°. Since the ray hits the inner surface at 45° (which is greater than the critical angle), it undergoes Total Internal Reflection (TIR).

Reflected and Emergent Ray: The ray reflects completely off this internal surface. It then travels to the third face of the prism and emerges out.

Labelling: The diagram should be clearly labelled with: Prism (30°, 60°, 90°), Incident Ray (Normal Incidence), Point of Internal Incidence (angle of incidence = 45°), Totally Internally Reflected Ray, Emergent Ray, and the Normal at the point of internal incidence.

Question 25: Two isosceles right –angles glass prisms are placed near each other as shown in Fig. 4.63. Complete the path of the light ray entering the first prism till it emerges out of the second prism.  

Ans:

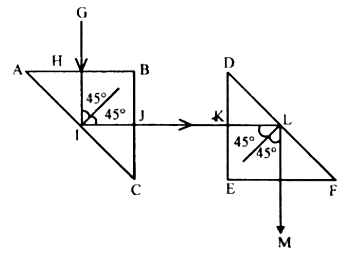
When the light ray enters the first prism perpendicular to its surface, it passes into the glass without bending. Inside the first prism, the ray strikes the hypotenuse face at an angle of 45°, which is greater than the critical angle of glass (approximately 42°). This causes the ray to undergo Total Internal Reflection (TIR), bending it through a 90° angle downwards.

This totally internally reflected ray then exits the first prism through its vertical face. Since it exits perpendicular to that face, it emerges into the air without bending.

The ray then travels horizontally and enters the second prism perpendicularly through its vertical face, so again, it enters without bending. Inside the second prism, it strikes the hypotenuse face at 45°, which again exceeds the critical angle. A second TIR occurs, bending the ray upwards by 90°.

Finally, the ray exits the second prism through its bottom face. As it is perpendicular to this face, it emerges straight into the air without any further deviation. The complete path of the light ray is therefore two connected “Z” shapes.

MULTIPLE CHOICE TYPE:  

Question 1: The critical angle for glass-air interface is: 

(a) 24°  

(b) 48° 

 (c) 42°   

(d) 45° 

Ans: (c)  42°    

Question 2: A total reflecting right angled isosceles prism can be used to deviate a ray of light through: 

(a) 30° 

 (b) 60°  

(c) 75° 

 (d) 90°.

Ans:(d) 90°.

Question 3: A total reflecting equilateral prism can be used to deviate a ray of light through: 

(a) 30°   

(b) 60°   

(c) 75°  

 (d) 90° 

Ans: (b) 60°