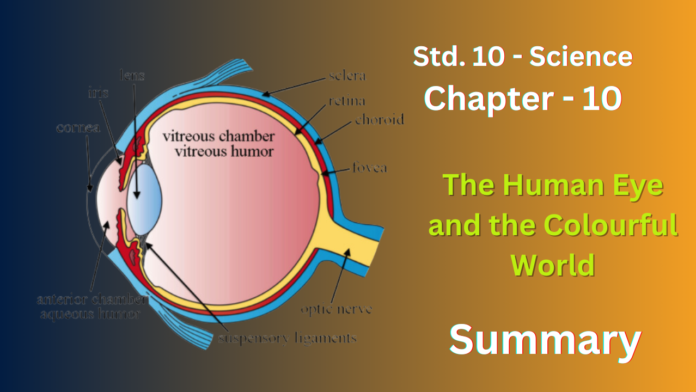
Here’s a summary of the chapter “The Human Eye and the Colourful World” from the 10th standard science syllabus:The Eye: A Light Detecting Organ The human eye is a complex and valuable sensory organ that allows us to see the world around us.It plays a crucial role in our perception of light, color, and depth. Structure of the Eye: The eye is approximately spherical in shape and is protected by the eyelid, eyelashes, and bony socket.Key parts of the eye include: Cornea: The transparent outer layer that refracts light entering the eye.Iris: The colored diaphragm that controls the amount of light entering the pupil.Pupil: The dark circular opening in the center of the iris that regulates light.Crystalline Lens: A transparent, flexible lens that further focuses light rays onto the retina.Retina: The light-sensitive inner layer containing photoreceptor cells (rods and cones) that convert light energy into electrical signals.Optic Nerve: A bundle of nerve fibers that transmits electrical signals from the retina to the brain for visual processing. The Working of the Eye Light enters the eye through the cornea and pupil.The cornea and lens refract (bend) the light rays, focusing them onto the retina.The retina contains photoreceptor cells called rods and cones. Rods: Responsible for vision in dim light (night vision).Cones: Responsible for color vision and vision in bright light. Rods and cones convert light energy into electrical signals.These electrical signals are transmitted through the optic nerve to the brain, where they are interpreted as vision. Accommodation The ability of the eye to adjust its focal length to focus on objects at different distances is called accommodation.The crystalline lens changes shape to achieve this.With age, the ability to accommodate decreases, leading to a condition called presbyopia (difficulty focusing on near objects). Refractive Errors Common refractive errors of the eye include: Myopia (nearsightedness): Difficulty seeing distant objects clearly. Corrected by using concave lenses.Hypermetropia (farsightedness): Difficulty seeing near objects clearly. Corrected by using convex lenses.Astigmatism: Blurred vision at all distances due to an irregularly shaped cornea. Corrected by using cylindrical lenses. The World of Color White light is composed of a spectrum of different colors with varying wavelengths.The cones in the retina are sensitive to different wavelengths of light, allowing us to perceive color.When all wavelengths of light stimulate the cones equally, we see white light.When specific wavelengths are selectively absorbed, we perceive different colors. Taking Care of Our Eyes Maintaining good eye hygiene is essential.Regular eye checkups are crucial to detect and address any vision problems early.A balanced diet rich in vitamins and minerals is important for eye health.Limiting screen time and taking breaks from close work can help prevent eye strain. Questions (Page 164)1. What is meant by power of accommodation of the eye ?Ans : The power of accommodation of the eye refers to its remarkable ability to adjust its focal length to bring objects at various distances into clear focus on the retina.2. A person with a myopic eye cannot see objects beyond 1.2 m distinctly. What should be the type of the corrective lens used to restore proper vision ?Ans : A person with myopia, also known as nearsightedness, has difficulty seeing distant objects clearly. In this scenario, the person cannot see objects beyond 1.2 meters distinctly.To restore proper vision for distant objects, the corrective lens needed is a concave lens.3. What is the far point and near point of the human eye with normal vision ?Ans : Far point: Infinity (represented by the symbol ∞)Near point: Approximately 25 centimeters (cm)4. A student has difficulty reading the blackboard while sitting in the last row. What could be the defect the child is suffering from ? How can it be corrected?Ans : The student’s difficulty reading the blackboard while sitting in the last row suggests a vision defect called myopia, also known as nearsightedness.Questions:1. The human eye can focus objects at different distances by adjusting the focal length of the eye lens. This is due to(a) presbyopia(b) accommodation(c) near – sightedness(d) far – sightednessAns : (b) accommodation2. The human eye forms the image of an object at its(a) cornea(b) iris(c) pupil(d) retinaAns : (d) retina3. The least distance of distinct vision for a young adult with normal vision is about(a) 25 m(b) 2.5 cm(c) 25 cm(d) 2.5 mAns : (c) 25 cm.4. The change in focal length of an eye lens is caused by the action of the(a) pupil(b) retina(c) ciliary muscles(d) irisAns : (c) ciliary muscles
5. A person needs a lens of power -5.5 dioptres for correcting his distant vision. For correcting his near vision he needs a lens of power +1.5 dioptre. What is the focal length of the lens required for correcting (i) distant vision, and (ii) near vision ?
Ans :
Focal Length (f) in meters = 1 / Power (D) in dioptres
Given:
- Power for distant vision (D₁): -5.5 dioptres (negative sign indicates diverging lens)
- Power for near vision (D₂): +1.5 dioptres (positive sign indicates converging lens)
Focal Length for Distant Vision (f₁):
- f₁ = 1 / D₁ = 1 / (-5.5 dioptres)
- f₁ ≈ -0.182 meters (negative sign signifies diverging lens)
Focal Length for Near Vision (f₂):
- f₂ = 1 / D₂ = 1 / (+1.5 dioptres)
- f₂ = 0.667 meters (positive sign signifies converging lens)
In conclusion:
- The focal length of the lens required for correcting distant vision is approximately -0.182 meters (diverging lens).
- The focal length of the lens required for correcting near vision is 0.667 meters (converging lens).
6. The far point of a myopic person is 80 cm in front of the eye. What is the nature and power of the lens required to correct the problem ?
Ans : A myopic person has difficulty seeing distant objects clearly. In this scenario, the far point is only 80 cm, indicating blurry vision beyond that distance.
We can use the lens formula to determine the power (P) of the lens needed for correction. However, for this specific case, we can reach a qualitative conclusion without needing an exact power calculation.
Lens Formula:
1/u + 1/v = 1/f
where:
- u = object distance (positive value for distant object)
- v = image distance (typically the far point of the eye, which is negative in this case)
- f = focal length of the lens (negative for a diverging lens)
Since the far point of the myopic person is only 80 cm (u = 0.8 m), the image formed by the eye falls in front of the retina (v is negative). To create a clear image on the retina, we need a lens that diverges the incoming rays so they focus at the far point (v = -0.8 m).
7. Make a diagram to show how hypermetropia is corrected. The near point of a hypermetropic eye is 1 m. What is the power of the lens required to correct the defect ? Assume that the near point of the normal eye is 25 cm.
Ans :
This diagram illustrates how a convex lens corrects hypermetropia (farsightedness).
Explanation:
- Hypermetropic Eye: In a hypermetropic eye, the eyeball is too short or the cornea is not curved enough. This causes light rays from nearby objects to focus behind the retina, resulting in blurred near vision.
- Light Rays: Parallel light rays from a near object (represented by the blue arrow) enter the hypermetropic eye.
- Focus Behind Retina: Due to the eye’s shape, these rays converge behind the retina, forming a blurry image.
- Convex Lens: A convex lens (converging lens) is placed in front of the eye.
- Refraction: The convex lens refracts (bends) the incoming light rays even more, converging them closer to the retina.
- Image on Retina: With the help of the convex lens, the light rays focus on the retina, forming a clear image of the near object.
Lens Power Calculation:
We can estimate the power (P) of the lens required using the formula:
P = 1 / f (in dioptres)
where:
- P = lens power in dioptres (unknown)
- f = focal length of the lens in meters (unknown)
However, with the given information, we can determine the relative power of the lens needed.
Given:
- Near point of hypermetropic eye (u) = 1 meter (m)
- Near point of normal eye (v) = 25 cm = 0.25 m
8. Why is a normal eye not able to see clearly the objects placed closer than 25 cm ?
Ans : A normal eye has a limited ability to focus on objects extremely close due to a combination of factors related to the structure and function of the eye’s focusing mechanism.
9. What happens to the image distance in the eye when we increase the distance of an object from the eye ?
Ans : When we increase the distance of an object from the eye in a healthy eye with normal accommodation, the image distance in the eye remains constant. This is because the eye’s lens actively adjusts its shape to maintain focus on the object and project a clear image onto the retina.
10. Why do stars twinkle ?
Ans : Stars twinkle because Earth’s atmosphere acts like a wobbly lens, bending starlight and making the star’s image flicker from our view. Planets, being closer and appearing larger, twinkle less due to this atmospheric effect.
11. Explain why the planets do not twinkle ?
Ans : Planets generally don’t twinkle like stars because of two key reasons:
- Distance: Stars are incredibly distant point sources of light, whereas planets are much closer to Earth. This larger distance makes starlight more susceptible to the twinkling effect caused by Earth’s atmosphere.
- Apparent Size: Planets appear as small discs in the night sky, while stars resemble tiny points of light. The twinkling effect from atmospheric bending is averaged out across the larger planetary disc, making planets appear steadier.
In simpler terms, stars are faraway like faint points of light, easily affected by atmospheric wobbles. Planets are closer and appear as small discs, less affected by the twinkling effect.
12. Why does the sun appear reddish early in the morning ?
Ans : The sunrise appears reddish because sunlight travels through more air at that angle. Earth’s atmosphere scatters blue light more than red light, so the red light reaches our eyes more easily, making the sun look red.
13. Why does the sky appear dark instead of blue to an astronaut ?
Ans : Astronauts see a black sky because space has no air to scatter sunlight. Without the blue scattering, the sky appears dark. They might see the bright sun itself, but the emptiness of space is black.