Chapter 14: Probability
Basic Concepts:
- Experiment.
- Sample Space: The set of all possible outcomes of an experiment.
- Event: A subset of the sample space.
- Probability of an Event: The number of favorable outcomes divided by the total number of possible outcomes.
Probability Rules:
- Addition Rule: For mutually exclusive events A and B, P(A or B) = P(A) + P(B).
- Multiplication Rule: For independent events A and B, P(A and B) = P(A) * P(B).
- Conditional Probability: The probability of event B occurring given that event A has already occurred.
Conditional Probability and Bayes’ Theorem:
- Conditional Probability: P(B|A) = P(A and B) / P(A).
- Bayes’ Theorem: P(A|B) = (P(B|A) * P(A)) / P(B).
Random Variables:
- Random Variable: A variable whose value depends on the outcome of a random experiment.
- Probability Distribution: A table or graph that shows the possible values of a random variable and their corresponding probabilities.
Probability Distributions:
- Discrete Probability Distribution: A probability distribution for a discrete random variable.
- Continuous Probability Distribution: A probability distribution for a continuous random variable.
- Binomial Distribution: A probability distribution for the number of successes in n independent Bernoulli trials.
- Poisson Distribution: A probability distribution for the number of occurrences of an event in a fixed interval of time or space.
- Normal Distribution: A continuous probability distribution that is often used to model real-world data.
Key Concepts:
- Probability of events
- Conditional probability and Bayes’ theorem
- Random variables and probability distributions
- Binomial and Poisson distributions
- Normal distribution
Exercise 14.1
1. A die is rolled. Let E be the event “die shows 4” and F be the event “die shows even number”. Are E and F mutually exclusive?
Ans :
2. A die is thrown. Describe the following events:
(i) A: a number less than 7
(ii) B: a number greater than 7
(iii) C: a multiple of 3
(iv) D: a number less than 4
(v) E: an even number greater than 4
(vi) F: a number not less than 3
Also find A ∪ B, A ∩ B, B ∪ C, E ∩ F, D ∩ E, A – C, D – E, E ∩ F′, F′
Ans :
A: {1, 2, 3, 4, 5, 6}
B: {} (empty set)
C: {3, 6}
D: {1, 2, 3}
E: {6}
F: {3, 4, 5, 6}
A ∪ B = {1, 2, 3, 4, 5, 6}
A ∩ B = {}
B ∪ C = {3, 6}
E ∩ F = {6}
D ∩ E = {}
A – C = {1, 2, 4, 5}
D – E = {1, 2, 3}
F‘ = {1, 2}
3. An experiment involves rolling a pair of dice and recording the numbers that come up. Describe the following events:
A: the sum is greater than 8, B: 2 occurs on either die
C: the sum is at least 7 and a multiple of 3.
Which pairs of these events are mutually exclusive?
Ans :
4. Three coins are tossed once. Let A denote the event ‘three heads show”, B denote the event “two heads and one tail show”, C denote the event” three tails show and D denote the event ‘a head shows on the first coin”. Which events are
(i) mutually exclusive? (ii) simple? (iii) Compound?
Ans :
5. Three coins are tossed. Describe
(i) Two events which are mutually exclusive.
(ii) Three events which are mutually exclusive and exhaustive.
(iii) Two events, which are not mutually exclusive.
(iv) Two events which are mutually exclusive but not exhaustive.
(v) Three events which are mutually exclusive but not exhaustive.
Ans :
(i) Two events which are mutually exclusive:
- A: All three coins show heads.
- B: All three coins show tails.
These events are mutually exclusive because they cannot occur simultaneously. If all three coins show heads, it’s impossible for all three to show tails and vice versa.
(ii) Three events which are mutually exclusive and exhaustive:
- A: All three coins show heads.
- B: Two heads and one tail show.
- C: One head and two tails show.
These three events cover all possible outcomes of tossing three coins, and no two of them can occur simultaneously. Therefore, they are mutually exclusive and exhaustive.
(iii) Two events which are not mutually exclusive:
- A: At least two coins show heads.
- B: The first coin shows heads.
These events are not mutually exclusive because it’s possible for both to occur simultaneously (e.g., two heads and one tail).
(iv) Two events which are mutually exclusive but not exhaustive:
- A: All three coins show heads.
- B: All three coins show tails.
As mentioned in (i), these events are mutually exclusive. However, they are not exhaustive because there are other possible outcomes, such as two heads and one tail or one head and two tails.
(v) Three events which are mutually exclusive but not exhaustive:
- A: All three coins show heads.
- B: All three coins show tails.
- C: Exactly one coin shows heads.
6. Two dice are thrown. The events A, B and C are as follows:
A: getting an even number on the first die.
B: getting an odd number on the first die.
C: getting the sum of the numbers on the dice ≤ 5.
Describe the events
(i) A′ (ii) not B (iii) A or B (iv) A and B (v) A but not C
(vi) B or C (vii) B and C (viii) A ∩ B′ ∩ C′
Ans :
7. Refer to question 6 above, state true or false: (give reason for your answer)
(i) A and B are mutually exclusive
(ii) A and B are mutually exclusive and exhaustive
(iii) A = B′ (iv) A and C are mutually exclusive
(v) A and B′ are mutually exclusive.
(vi) A′, B′, C are mutually exclusive and exhaustive.
Ans :
(i) A and B are mutually exclusive.
True.
An even number and an odd number cannot occur simultaneously on the first die. Therefore, A and B are mutually exclusive.
(ii) A and B are mutually exclusive and exhaustive.
True.
As we established in (i), A and B are mutually exclusive. Additionally, since every outcome on the first die is either even or odd, A and B together cover all possible outcomes, making them exhaustive.
(iii) A = B’.
True.
A’ represents the complement of A, which means “not A.” Since A is the event of getting an even number on the first die, A’ is the event of getting an odd number on the first die. This is equivalent to event B. Therefore, A = B’.
(iv) A and C are mutually exclusive.
False.
It’s possible to have an even number on the first die (A) and a sum ≤ 5 (C) at the same time. For example, (2, 3) satisfies both conditions.
(v) A and B′ are mutually exclusive.
True.
A is the event of getting an even number on the first die, and B’ is the event of getting an even number on the first die (since B is the event of getting an odd number). Therefore, A and B’ are the same event, and since an event cannot be mutually exclusive with itself, A and B’ are mutually exclusive.
(vi) A′, B′, C are mutually exclusive and exhaustive.
False.
While A’, B’, and C are mutually exclusive (no two can occur simultaneously), they are not exhaustive. There are other possible outcomes, such as (3, 6) and (4, 5), that do not fall into any of these categories.
Exercise 14.2
1.
Ans :
(a): All probabilities are between 0 and 1, and their sum is 0.1 + 0.01 + 0.05 + 0.03 + 0.01 + 0.2 + 0.6 = 1. This is a valid assignment.
(b): All probabilities are equal to 1/7, and there are 7 outcomes. Since 1/7 * 7 = 1, this is a valid assignment.
(c): All probabilities are between 0 and 1, and their sum is 0.1 + 0.2 + 0.3 + 0.4 + 0.5 + 0.6 + 0.7 = 2.8. Since the sum is greater than 1, this is not a valid assignment.
(d): One probability is negative (-0.1), violating the non-negativity condition. This is not a valid assignment.
(e): All probabilities are positive, and their sum is 1/14 + 2/14 + 3/14 + 4/14 + 5/14 + 6/14 + 15/14 = 46/14 = 7/2. Since the sum is greater than 1, this is not a valid assignment.
2. A coin is tossed twice, what is the probability that atleast one tail occurs?
Ans :
3. A die is thrown, find the probability of following events:
(i) A prime number will appear,
(ii) A number greater than or equal to 3 will appear,
(iii) A number less than or equal to one will appear,
(iv) A number more than 6 will appear,
(v) A number less than 6 will appear
Ans :
Given: A die is thrown.
Sample space: {1, 2, 3, 4, 5, 6}
(i)
Prime numbers on a die are 2, 3, and 5. So, there are 3 favorable outcomes.
Probability = (Number of favorable outcomes) / (Total number of outcomes)
= 3/6
= 1/2
(ii)
Numbers greater than or equal to 3 are 3, 4, 5, and 6. So, there are 4 favorable outcomes.
Probability = 4/6
= 2/3
(iii)
Only 1 is less than or equal to 1. So, there is 1 favorable outcome.
Probability = 1/6
(iv)
There are no numbers on a die greater than 6. So, there are 0 favorable outcomes.
Probability = 0
(v)
Numbers less than 6 are 1, 2, 3, 4, and 5. So, there are 5 favorable outcomes.
Probability = ⅚
4. A card is selected from a pack of 52 cards.
(a) How many points are there in the sample space?
(b) Calculate the probability that the card is an ace of spades.
(c) Calculate the probability that the card is (i) an ace (ii) black card.
Ans :
(a) When a card is selected from a pack of 52 cards, there are 52 possible outcomes.
(b) Probability = (Number of favorable outcomes) / (Total number of outcomes) = 1/52
(c) (i) an ace (ii) a black card.
(i) An ace
There are 4 aces
Probability = 4/52 = 1/13
(ii) A black card
There are 26 black cardsx
Probability = 26/52 = ½
5. A fair coin with 1 marked on one face and 6 on the other and a fair die are both tossed. find the probability that the sum of numbers that turn up is (i) 3 (ii) 12
Ans :
Given: A fair coin and a fair die are tossed.
(i) Probability of a sum of 3
To get a sum of 3, the coin must show 1 and the die must show 2.
- Probability of getting 1 on the coin: 1/2
- Probability of getting 2 on the die: 1/6
Probability = (1/2) * (1/6) = 1/12
(ii) Probability of a sum of 12
To get a sum of 12, the coin must show 6 and the die must show 6.
- Probability of getting 6 on the coin: 1/2
- Probability of getting 6 : 1/6
So, the probability of a sum of 12 is:
Probability = (1/2) * (1/6) = 1/12
6. There are four men and six women on the city council. If one council member is selected for a committee at random, how likely is it that it is a woman?
Ans :
Total council members: 4 men + 6 women = 10 members
Probability of selecting a woman:
Number of women / Total number of members = 6 / 10 = 3/5
Therefore, the probability of selecting a woman for the committee is 3/5.
7. A fair coin is tossed four times, and a person win Re 1 for each head and lose Rs 1.50 for each tail that turns up.
From the sample space calculate how many different amounts of money you can have after four tosses and the probability of having each of these amounts.
Ans :
Given: A fair coin is tossed four times.
Winnings: Re 1 for each head, Rs 1.50 for each tail.
Sample space:
- 2^4 = 16 possible outcomes (since there are 2 possible outcomes for each toss)
Possible amounts of money:
The minimum amount is -6 (losing 4 tails), and the maximum is 4 (winning 4 heads).
- -6: Losing all 4 tosses (TTTT)
- -4.5: Losing 3 tosses (THTT, TTHT, THTT)
- -3: Losing 2 tosses (HHTT, THTH, TTHH, HTHT)
- -1.5: Losing 1 toss (HHHT, HHTH, HTHH, THHH)
- 0: No net gain or loss (HTHT, THTH, HTHH, THHH)
- 1.5: Winning 1 toss (HTTT, THTT, TTHT)
- 3: Winning 2 tosses (HHTT, THTH, TTHH)
- 4.5: Winning 3 tosses (HHHT, HHTH, HTHH)
- 6: Winning all 4 tosses (HHHH)
Probability of each amount:
- -6: 1/16 (only 1 outcome: TTTT)
- -4.5: 3/16 (3 outcomes: THTT, TTHT, HTTT)
- -3: 3/16 (3 outcomes: HHTT, THTH, TTHH)
- -1.5: 4/16 = 1/4 (4 outcomes: HHHT, HHTH, HTHH, THHH)
- 0: 3/16 (3 outcomes: HTHT, THTH, THHH)
- 1.5: 3/16 (3 outcomes: HTTH, THTT, TTHT)
- 3: 3/16 (3 outcomes: HHTT, THTH, TTHH)
- 4.5: 3/16 (3 outcomes: HHHT, HHTH, HTHH)
- 6: 1/16 (only 1 outcome: HHHH)
8. Three coins are tossed once. Find the probability of getting
(i) 3 heads (ii) 2 heads (iii) atleast 2 heads (iv) atmost 2 heads (v) no head (vi) 3 tails (vii) exactly two tails (viii) no tail (ix) atmost two tails
Ans :
Given: Three coins are tossed once.
Sample space:
- HHH, HHT, HTH, HTT, THH, THT, TTH, TTT
(i) Probability of getting 3 heads
HHH
Probability = 1/8
(ii) Probability of getting 2 heads
There are 3 outcomes with two heads: HHT, HTH, THH
Probability = 3/8
(iii) Probability of getting at least 2 heads
This includes 3 heads (1 outcome) and 2 heads (3 outcomes)
Probability = 4/8 = 1/2
(iv) This includes 0 heads (1 outcome), 1 head (3 outcomes), and 2 heads (3 outcomes)
Probability = 7/8
(v) Probability of getting no heads
This is the same as getting 3 tails.
Probability = 1/8
(vi) Probability of getting 3 tails
no heads.
Probability = 1/8
(vii) Probability of getting exactly two tails
This is the same as getting one head.
Probability = 3/8
(viii) Probability of getting no tails
This is the same as getting 3 heads.
Probability = 1/8
(ix) Probability of getting at most two tails
This is the same as getting at least one head.
Probability = 7/8
9. If 2/11 is the probability of an event, what is the probability of the event ‘not A’.
Ans :
The probability of the event “not A” is 1 – P(A).
Since P(A) = 2/11, then P(not A) = 1 – 2/11 = 9/11.
10. A letter is chosen at random from the word ‘ASSASSINATION’. Find the probability that letter is (i) a vowel (ii) a consonant
Ans :
Given: The word “ASSASSINATION”
(i) Probability of a vowel
Vowels in the word are: A, A, A, I, I, O
Total vowels = 6
Total letters = 13
Probability of a vowel = Number of vowels / Total number of letters = 6/13
(ii) Probability of a consonant
Consonants in the word are:
S, S, S, S, N, T, N
Total consonants = 7
Probability of a consonant = Number of consonants / Total number of letters = 7/13
11. In a lottery, a person choses six different natural numbers at random from 1 to 20, and if these six numbers match with the six numbers already fixed by the lottery committee, he wins the prize. What is the probability of winning the prize in the game? [Hint order of the numbers is not important.]
Ans :
12. Check whether the following probabilities P(A) and P(B) are consistently defined
(i) P(A) = 0.5, P(B) = 0.7, P(A ∩ B) = 0.6
(ii) P(A) = 0.5, P(B) = 0.4, P(A ∪ B) = 0.8
Ans :
Analyzing each case:
(i) P(A) = 0.5, P(B) = 0.7, P(A ∩ B) = 0.6
- All probabilities are non-negative.
- P(A ∪ B) ≤ P(A) + P(B) becomes 0.6 ≤ 0.5 + 0.7, which is true.
Therefore, the probabilities in (i) are consistently defined.
(ii) P(A) = 0.5, P(B) = 0.4, P(A ∪ B) = 0.8
- All probabilities are non-negative.
- P(A ∪ B) ≤ P(A) + P(B) becomes 0.8 ≤ 0.5 + 0.4, which is true.
13.
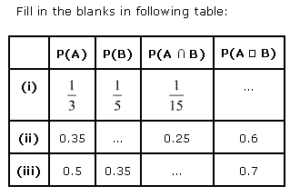
Ans :
14. Given P(A) = 3/5 and P(B) = 1/5 . Find P(A or B), if A and B are mutually exclusive events.
Ans :
If A and B are mutually exclusive events, then P(A or B) = P(A) + P(B).
Therefore, given P(A) = 3/5 and P(B) = 1/5, and knowing they are mutually exclusive, we can find P(A or B) as follows:
P(A or B) = P(A) + P(B) = 3/5 + 1/5 = 4/5
So, the probability of event A or B occurring is 4/5.
15. If E and F are events such that P(E) = 1/4 , P(F) = 1/2 and P(E and F) =1/8 , find
(i) P(E or F), (ii) P(not E and not F).
Ans :
Given:
- P(E) = 1/4
- P(F) = 1/2
- P(E ∩ F) = 1/8
(i) P(E or F)
P(E or F) = P(E) + P(F) – P(E ∩ F)
Substituting the given values:
P(E or F) = 1/4 + 1/2 – 1/8
= 5/8
(ii) P(not E and not F)
This is equivalent to the complement of the union of E and F, which can be written as:
P(not E and not F) = P((E ∪ F)’)
Using the complement rule:
P(not E and not F) = 1 – P(E ∪ F)
Substituting the value we found in (i):
P(not E and not F) = 1 – 5/8
= 3/8
16. Events E and F are such that P(not E or not F) = 0.25, State whether E and F are mutually exclusive.
Ans :
17. A and B are events such that P(A) = 0.42, P(B) = 0.48 and P(A and B) = 0.16. Determine (i) P(not A), (ii) P(not B) and (iii) P(A or B)
Ans :
Given:
- P(A) = 0.42
- P(B) = 0.48
- P(A ∩ B) = 0.16
(i) P(not A)
P(not A) = 1 – P(A) = 1 – 0.42 = 0.58
(ii) P(not B)
P(not B) = 1 – P(B) = 1 – 0.48 = 0.52
(iii) P(A or B)
P(A or B) = P(A) + P(B) – P(A ∩ B)
= 0.42 + 0.48 – 0.16
= 0.74
18. In Class XI of a school 40% of the students study Mathematics and 30% study Biology. 10% of the class study both Mathematics and Biology. If a student is selected at random from the class, find the probability that he will be studying Mathematics or Biology
Ans :
o find the probability that a student is studying Mathematics or Biology, we can use the formula:
P(A or B) = P(A) + P(B) – P(A and B)
where:
- P(A) is the probability of studying Mathematics
- P(B) is the probability of studying Biology
- P(A and B) is the probability of studying both Mathematics and Biology
Given:
- P(A) = 40% = 0.4
- P(B) = 30% = 0.3
- P(A and B) = 10% = 0.1
Substituting these values into the formula:
P(A or B) = 0.4 + 0.3 – 0.1 = 0.6
Therefore, the probability that a randomly selected student from the class is studying Mathematics or Biology is 0.6.
19. In an entrance test that is graded on the basis of two examinations, the probability of a randomly chosen student passing the first examination is 0.8 and the probability of passing the second examination is 0.7. The probability of passing atleast one of them is 0.95. What is the probability of passing both?
Ans :
We are given:
- P(A) = 0.8
- P(B) = 0.7
- P(A ∪ B) = 0.95
We need to find P(A ∩ B).
We can use the formula:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Substituting the given values:
0.95 = 0.8 + 0.7 – P(A ∩ B)
Solving for P(A ∩ B):
P(A ∩ B) = 0.8 + 0.7 – 0.95 = 0.55
Therefore, the probability of passing both examinations is 0.55.
20. The probability that a student will pass the final examination in both English and Hindi is 0.5 and the probability of passing neither is 0.1. If the probability of passing the English examination is 0.75, what is the probability of passing the Hindi examination?
Ans :
We are given:
- P(E ∩ H) = 0.5
- P(E ∪ H)’ = 0.1
We need to find P(H).
First, we can find P(E ∪ H) using the complement rule:
P(E ∪ H) = 1 – P(E ∪ H)’ = 1 – 0.1 = 0.9
Now, we can use the formula:
P(E ∪ H) = P(E) + P(H) – P(E ∩ H)
Substituting the given values:
0.9 = 0.75 + P(H) – 0.5
Solving for P(H):
P(H) = 0.9 – 0.75 + 0.5 = 0.65
Therefore, the probability of passing the Hindi examination is 0.65.
21. In a class of 60 students, 30 opted for NCC, 32 opted for NSS and 24 opted for both NCC and NSS. If one of these students is selected at random, find the probability that
(i) The student opted for NCC or NSS.
(ii) The student has opted neither NCC nor NSS.
(iii) The student has opted NSS but not NCC.
Ans :
Given:
- Total students = 60
- Students opted for NCC = 30
- Students opted for NSS = 32
- Students opted for both NCC and NSS = 24
(i) Probability of opting for NCC or NSS
Using the formula:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
where:
- A: opting for NCC
- B: opting for NSS
Substituting the given values:
P(A ∪ B) = 30/60 + 32/60 – 24/60 = 38/60 = 19/30
(ii) Probability of opting neither NCC nor NSS
This is the complement of the event “opting for NCC or NSS”.
P(not A and not B) = 1 – P(A ∪ B) = 1 – 19/30 = 11/30
(iii) Probability of opting for NSS but not NCC
This is the difference between the total number of students opting for NSS and the number of students opting for both NCC and NSS.
P(NSS but not NCC) = (Number of students opting for NSS) – (Number of students opting for both)
= 32/60 – 24/60 = 8/60 = 2/15


