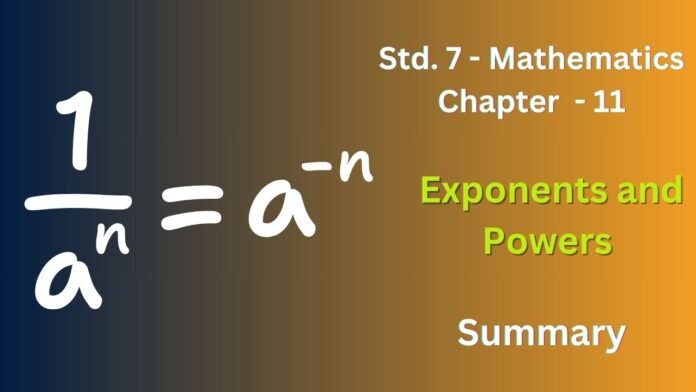Exponents are a shorthand way of representing repeated multiplication.
- Base: The number being multiplied repeatedly.
- Exponent: The small raised number that indicates how many times the base is multiplied by itself.
For example:
- In 2³, 2 is the base and 3 is the exponent.
- 2³ = 2 × 2 × 2 = 8
Powers are the results of using exponents. For instance, 8 is the power of 2 in the example above.
Laws of Exponents
- Product rule: a^m × a^n = a^(m+n)
- Quotient rule: a^m / a^n = a^(m-n)
- Power of a power rule: (a^m)^n = a^(m*n)
- Zero exponent rule: a^0 = 1
- Negative exponent rule: a^-n = 1 / a^n
Understanding these laws helps simplify expressions with exponents and perform calculations efficiently.
Applications
- Scientific notation: Used to represent very large or very small numbers.
- Computer science: Used in data storage and processing.
- Finance: Used in compound interest calculations.
By mastering exponents and powers, you gain a valuable tool for solving mathematical problems and understanding various real-world applications.
Exercise 11.1
1. Find the value of
(i) 26
(ii) 93
(iii) 112
(iv) 54
Ans :
Calculations:
(i) 2⁶ = 2 × 2 × 2 × 2 × 2 × 2 = 64
(ii) 9³ = 9 × 9 × 9 = 729
(iii) 11² = 11 × 11
= 121
(iv) 5⁴ = 5 × 5 × 5 × 5 = 625
2. express the following in exponential form:
(i) 6 × 6 × 6 × 6
(ii) t × t
(iii) b × b × b × b
(iv) 5 × 5 × 7 × 7 × 7
(v) 2 × 2 × a × a
(vi) a × a × a × c × c × c× c × d
Ans :
(i) 6 × 6 × 6 × 6 = 6⁴
(ii) t × t = t²
(iii) b × b × b × b = b⁴
(iv) 5 × 5 × 7 × 7 × 7 = 5² × 7³
(v) 2 × 2 × a × a = 2² × a²
(vi) a × a × a × c × c × c × c × d = a³ × c⁴ × d
3. Express each of the following numbers using exponential notation:
(i) 512
(ii) 343
(iii) 729
(iv) 3125
Ans :
(i) 512
- Prime factorization of 512 is
- 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
- So, 512 = 2⁹
(ii) 343
- Prime factorization of 343 is
- 7 × 7 × 7
- So, 343 = 7³
(iii) 729
- Prime factorization of 729 is
- 3 × 3 × 3 × 3 × 3 × 3
- So, 729 = 3⁶
(iv) 3125
- Prime factorization of 3125 is
- 5 × 5 × 5 × 5 × 5
- So, 3125 = 5⁵
4. Identify the greater number, wherever possible, in each of the following?
(i) 4³ or 3⁴
(ii) 5³ or 3⁵
(iii) 2⁸ or 8²
(iv) 100² or 2¹⁰⁰
(v) 2¹⁰ or 10²
Ans :
(i) 4³ or 3⁴
- 4³ = 64
- 3⁴= 81
- 3⁴ is greater than 4³
(ii) 5³ or 3⁵
- 5³ =125
- 3⁵ =243
- 3⁵ is greater than 5³
(iii) 2⁸ or 8²
- 2⁸ =256
- 8²= 64
- 2⁸ is greater than 8²
(iv) 100² or 2¹⁰⁰
- 100² =10,000
- 2¹⁰⁰ is a too large number
- 2¹⁰⁰ is greater than 100²
(v) 2¹⁰ or 10²
- 2¹⁰ = 1024
- 10² = 100
- 2¹⁰ is greater than 10²
5. Express each of the following as the product of powers of their prime
(i) 648
(ii) 405
(iii) 540
(iv) 3600
Ans :
i) 648
- Prime factorization: 2 × 2 × 2 × 3 × 3 × 3 × 3
- Exponential form: 2³ × 3⁴
ii) 405
- Prime factorization: 3 × 3 × 3 × 3 × 5
- Exponential form: 3⁴ × 5
iii) 540
- Prime factorization: 2 × 2 × 3 × 3 × 3 × 5
- Exponential form: 2² × 3³ × 5
iv) 3600
- Prime factorization: 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5
- Exponential form: 2⁴ × 3² × 5²
6. Simplify:
(i) 2 × 10³
(ii) 7² × 2²
(iii) 2³ × 5
(iv) 3 × 4⁴
(v) 0 × 10²
(vi) 5² × 3³
(vii) 2⁴ × 3²
(viii) 3² × 10⁴
Ans :
Let’s simplify the given expressions:
(i) 2 × 10³
This can be written as 2 × 1000 = 2000
(ii) 7² × 2²
Applying the property, we get (7 * 2)² = 14² = 196
(iii) 2³ × 5
This can be written as 8 × 5 = 40
(iv) 3 × 4⁴
This can be written as 3 × 256 = 768
(v) 0 × 10²
Any number multiplied by 0 is 0. So, the answer is 0.
(vi) 5² × 3³
Applying the property, we get (5 * 3)^(2+3) = 15⁵ = 759375
(vii) 2⁴ × 3²
Applying the property, we get (2 * 3)^(4+2) = 6⁶ = 46656
(viii) 3² × 10⁴
This can be written as 9 × 10000 = 90000
7. Simplify:
(i) (-4)³
(ii) (-3) × (-2)³
(iii) (-3)² × (-5)²
(iv) (-2)³ × (-10)³
Ans :
(i) (-4)³ = (-4) × (-4) × (-4) = -64
(ii) (-3) × (-2)³ = (-3) × (-2) × (-2) × (-2) = (-3) × (-8) = 24
(iii) (-3)² × (-5)² = (-3) × (-3) × (-5) × (-5)
= 9 × 25 = 225
(iv) (-2)³ × (-10)³ = (-2) × (-2) × (-2) × (-10) × (-10) × (-10) = (-8) × (-1000) = 8000
8. Compare the following:
(i) 2.7 × 10¹² and 1.5 × 10⁸
(ii) 4 × 10¹⁴ and 3 × 10¹⁷
Ans :
(i) 2.7 × 10¹² and 1.5 × 10⁸
- Focus on the exponents: 12 is greater than 8.
- Conclusion:
2.7 × 10¹² is greater than 1.5 × 10⁸.
(ii) 4 × 10¹⁴ and 3 × 10¹⁷
- Focus on the exponents: 17 is greater than 14.
- Conclusion: 3 × 10¹⁷ is greater than 4 × 10¹⁴.
Exercise 11.2
1. Using laws of e×ponents, simplify and write the answer in e×ponential form:
(i) 3² × 3⁴ × 3⁸
(ii) 6¹⁵ ÷ 6¹⁰
(iii) a³ × a²
(iv) 7^x × 7²
(v) (5²)³ ÷ 5³
(vi) 2⁵ × 5⁵
(vii) a⁴ × b⁴
(viii) (3⁴)³
(ix) (2²⁰ ÷ 2¹⁵) × 2³
(x) 8^t ÷ 8²
Ans :
- Product rule: a^m * a^n = a^(m+n)
- Quotient rule: a^m / a^n = a^(m-n)
- Power of a power rule: (a^m)^n = a^(m*n)
Let’s simplify the expressions:
(i) 3² × 3⁴ × 3⁸ Applying the product rule: = 3^(2+4+8) = 3¹⁴
(ii) 6¹⁵ ÷ 6¹⁰ Applying the quotient rule: = 6^(15-10) = 6⁵
(iii) a³ × a² Applying the product rule: = a^(3+2) = a⁵
(iv) 7^x × 7² Applying the product rule: = 7^(x+2)
(v) (5²)³ ÷ 5³ Applying the power of a power rule and then the quotient rule: = 5^(2*3) ÷ 5³ = 5⁶ ÷ 5³ = 5^(6-3) = 5³
(vi) 2⁵ × 5⁵
- There’s no simplification using exponent laws for different bases.
- So, the expression remains as 2⁵ × 5⁵
(vii) a⁴ × b⁴
- There’s no simplification using exponent laws for different bases.
- So, the expression remains as a⁴ × b⁴
(viii) (3⁴)³ Applying the power of a power rule: = 3^(4*3) = 3¹²
(ix) (2²⁰ ÷ 2¹⁵) × 2³ Applying the quotient rule first: = 2^(20-15) × 2³ = 2⁵ × 2³ Applying the product rule: = 2^(5+3) = 2⁸
(x) 8^t ÷ 8² Applying the quotient rule: = 8^(t-2)
2. Simplify and express each of the following in exponential form:
Ans :
Let’s simplify the expressions using the laws of exponents:
(i) (2³ × 3⁴ × 4) / (2 × 3²)
- Break down 4 into 2²:
- (2³ × 3⁴ × 2²) / (2 × 3²)
- Apply the product rule for the numerator:
- (2^(3+2) × 3⁴) / (2 × 3²)
- (2⁵ × 3⁴) / (2 × 3²)
- Apply the quotient rule for similar bases:
- 2^(5-1) × 3^(4-2)
- 2⁴ × 3²
(ii) [(5²)³ × 5⁴] ÷ 5⁷
- Apply the power of a power rule for the numerator:
- (5^(2*3) × 5⁴) ÷ 5⁷
- (5⁶ × 5⁴) ÷ 5⁷
- Apply the product rule for the numerator:
- 5^(6+4) ÷ 5⁷
- 5¹⁰ ÷ 5⁷
- Apply the quotient rule:
- 5^(10-7)
- 5³
(iii) 25⁴ ÷ 5³
- Express 25 as 5²:
- (5²)⁴ ÷ 5³
- Apply the power of a power rule:
- 5^(2*4) ÷ 5³
- 5⁸ ÷ 5³
- Apply the quotient rule:
- 5^(8-3)
- 5⁵
(iv) (3 × 7² × 11⁸) / (21 × 11³)
- Break down 21 into 3 × 7:
- (3 × 7² × 11⁸) / (3 × 7 × 11³)
- Cancel out common factors:
- 7^(2-1) × 11^(8-3)
- 7¹ × 11⁵
- 7 × 11⁵
(v) 3⁷ / (3⁴ × 3³)
- Apply the product rule for the denominator:
- 3⁷ / 3^(4+3)
- 3⁷ / 3⁷
- Any non-zero number divided by itself is 1:
- 1
(vi) 2⁰ + 3⁰ + 4⁰
- Any non-zero number raised to the power of 0 is 1:
- 1 + 1 + 1
- 3
(vii) 2⁰ × 3⁰ × 4⁰
- Any non-zero number raised to the power of 0 is 1:
- 1 × 1 × 1
- 1
(viii) (3⁰ + 2⁰) × 5⁰
- Calculate the values inside the parentheses first:
- (1 + 1) × 1
- 2 × 1
- 2
(ix) (2⁸ × a⁵) / (4³ × a³)
- Break down 4³ into 2⁶:
- (2⁸ × a⁵) / (2⁶ × a³)
- Apply the quotient rule for similar bases:
- 2^(8-6) × a^(5-3)
- 2² × a²
- 4a²
(x) (a⁵ / a³) × a⁸
- Apply the quotient rule for the first part:
- a^(5-3) × a⁸
- a² × a⁸
- Apply the product rule:
- a^(2+8)
- a¹⁰
(xi) (4⁵ × a⁸b³) / (4⁵ × a⁵b²)
- Cancel out common factors:
- a^(8-5) × b^(3-2)
- a³b
(xii) (2³ × 2)²
- Apply the product rule inside the parentheses:
- (2^(3+1))²
- (2⁴)²
- Apply the power of a power rule:
- 2^(4*2)
- 2⁸
3. true or false and justify your answer:
(i) 10 × 10¹¹ = 100¹¹
(ii) 2³ > 5²
(iii) 2³ × 3² = 6⁵
(iv) 3⁰ = (1000)⁰
Ans :
(i) 10 × 10¹¹ = 100¹¹
- False
- 10 × 10¹¹ = 10^(1+11) = 10¹²
- 100¹¹ = (10²)¹¹ = 10²²
- 10¹² ≠ 10²²
(ii) 2³ > 5²
- False
- 2³ = 8
- 5² = 25
- 8 < 25
(iii) 2³ × 3² = 6⁵
- False
- 2³ × 3²
- = 8 × 9
- = 72
- 6⁵ = 7776
- 72 ≠ 7776
(iv) 3⁰ = (1000)⁰
- True
- So, 3⁰ = 1 and (1000)⁰ = 1
4. Express each of the following as a product of prime factors only in exponential form:
(i) 108 × 192
(ii) 270
(iii) 729 × 64
(iv) 768
Ans :
Solutions:
(i) 108 × 192
- Prime factorization of 108: 2² × 3³
- Prime factorization of 192: 2⁶ × 3
- Multiplying both: (2² × 3³) × (2⁶ × 3)
- Combine like bases: 2^(2+6) × 3^(3+1)
- Final expression: 2⁸ × 3⁴
(ii) 270
- Prime factorization of 270: 2 × 3³ × 5
- Final expression: 2¹ × 3³ × 5¹
(iii) 729 × 64
- Prime factorization of 729: 3⁶
- Prime factorization of 64: 2⁶
- Multiplying both: 3⁶ × 2⁶
- Final expression: 3⁶ × 2⁶
(iv) 768
- Prime factorization of 768: 2⁸ × 3
- Final expression: 2⁸ × 3¹
5. Simplify:
Ans :
Exercise 11.3
1. Write the following numbers in the e×panded forms:
279404, 3006194, 2806196, 120719, 20068
Ans :
Let’s expand the given numbers:
i) 279404 = 2 x 100000 + 7 x 10000 + 9 x 1000 + 4 x 100 + 0 x 10 + 4 x 1
ii) 3006194 = 3 x 1000000 + 0 x 100000 + 0 x 10000 + 6 x 1000 + 1 x 100 + 9 x 10 + 4 x 1
iii) 2806196 = 2 x 1000000 + 8 x 100000 + 0 x 10000 + 6 x 1000 + 1 x 100 + 9 x 10 + 6 x 1
iv) 120719 = 1 x 100000 + 2 x 10000 + 0 x 1000 + 7 x 100 + 1 x 10 + 9 x 1
v) 20068 = 2 x 10000 + 0 x 1000 + 0 x 100 + 6 x 10 + 8 x 1
2. Find the number from each of the following expanded forms:
(a) 8 × 104 + 6 × 103 + 0 × 102 + 4 × 101 + 5 × 100
(b) 4 × 105 + 5 × 103 + 3 × 102 + 2 × 100
(c) 3 × 104 + 7 × 102 + 5 × 100
(d) 9 × 105 + 2 × 102 + 3 × 101
Ans :
(a) 8 × 10⁴ + 6 × 10³ + 0 × 10² + 4 × 10¹ + 5 × 10⁰
= 80000 + 6000 + 0 + 40 + 5
= 86045
(b) 4 × 10⁵ + 5 × 10³ + 3 × 10² + 2 × 10⁰
= 400000 + 5000 + 300 + 2
= 405302
(c) 3 × 10⁴ + 7 × 10² + 5 × 10⁰
= 30000 + 700 + 5
= 30705
(d) 9 × 10⁵ + 2 × 10² + 3 × 10¹
= 900000 + 200 + 30
= 900230
3. Express the following numbers in standard form:
(i) 5,00,00,000
(ii) 70,00,000
(iii) 3,18,65,00,000
(iv) 3,90,878
(v) 39087.8
(vi) 3908.78
Ans :
(i) 5,00,00,000
= 5 × 10000000
= 5 × 10⁷
(ii) 70,00,000
= 7 × 1000000
= 7 × 10⁶
(iii) 3,18,65,00,000
= 3.1865 × 100000000
= 3.1865 × 10⁸
(iv) 3,90,878
= 3.90878 × 100000
= 3.90878 × 10⁵
(v) 39087.8
= 3.90878 × 10000
= 3.90878 × 10⁴
(vi) 3908.78
= 3.90878 × 1000
= 3.90878 × 10³
4. Express the number appearing in the following statements in standard form:
(a) The distance between Earth and Moon is 384.0. 000 m.
(b) Speed of light in vacuum is 300,000,000 m/s.
(c) Diameter of the Earth is 1,27,56,000 m.
(d) Diameter of the Sun is 1,400,000,000 m.
(e) In a galaxy there are an average 100,000,000,000 stars.
(f) The universe is estimated to be about 12,000,000,000 years old.
(g) The distance of the Sun from the centre of the Milky Way Galaxy is estimated to be 300,000,000,000,000,000,000 m.
(h) 60,230,000,000,000,000,000,000 molecules are contained in a drop of water weighing 1.8 gm.
(i) The Earth has 1,353,000,000 cubic km of sea water.
(j) The population of India was about 1,027,000,000 in March 2001.
Ans :
(a) Standard form: 3.84 × 10⁸ m
(b) Standard form: 3 × 10⁸ m/s
(c) Standard form: 1.2756 × 10⁷ m
(d) Standard form: 1.4 × 10⁹ m
(e) Standard form: 1 × 10¹¹ stars
(f) Standard form: 1.2 × 10¹⁰ years
(g) Standard form: 3 × 10²⁰ m
(h) Standard form: 6.023 × 10²² molecules
(i) Standard form: 1.353 × 10⁹ cubic km
(j) Standard form: 1.027 × 10⁹ people