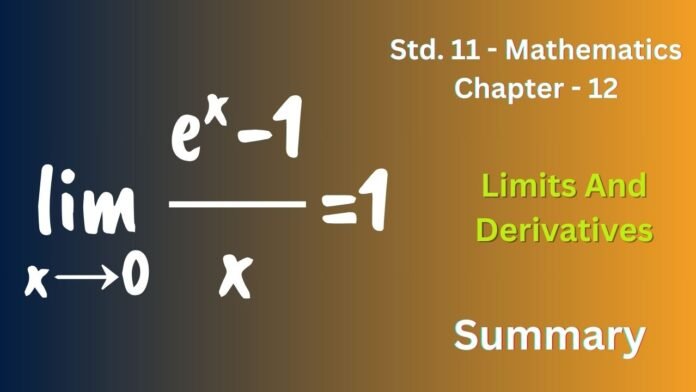NCERT Solutions for Class 11 Maths Chapter 12
Chapter 12.1: Introduction
- Limits: The concept of a limit is central to calculus and is used to describe the behavior of a function as its input approaches a certain value.
- Derivatives: Derivatives measure the rate of change of a function. They are essential for understanding concepts like velocity, acceleration, and slopes of curves.
Chapter 12.2: Limits of Functions
- Definition of Limit: The limit of a function f(x) as x approaches a is denoted by lim(x→a) f(x). It represents the value that f(x) approaches as x gets closer and closer to a.
- Left-hand and Right-hand Limits: These are limits taken from the left and right sides of a point, respectively.
- Existence of Limits: For a limit to exist, the left-hand and right-hand limits must be equal.
- Limit Laws: These are rules for evaluating limits of algebraic combinations of functions.
Chapter 12.3: Evaluation of Limits
- Methods of Evaluation: Direct substitution, factorization, rationalization, and using standard limits.
- Standard Limits: Important limits such as lim(x→0) sin(x)/x = 1 and lim(x→0) (1 – cos(x))/x = 0.
Chapter 12.4: Derivative
- Notation: f'(a) or dy/dx.
- Geometric Interpretation: The derivative at a point represents the slope of the tangent line to the graph of f(x) at that point.
Chapter 12.5: Differentiation
- Rules of Differentiation: Power rule, sum rule, difference rule, product rule, quotient rule, chain rule.
- Differentiation of Trigonometric Functions: Derivatives of sin(x), cos(x), tan(x), cot(x), sec(x), and csc(x).
Key Concepts:
- Limits and their evaluation
- Derivatives and their geometric interpretation
- Rules of differentiation
- Applications of derivatives (e.g., finding velocity, acceleration, tangent lines)
NCERT Solutions for Class 11 Maths Chapter 12
Exercise 12.1
Evaluate the following limits in Exercises 1 to 22.
1.
Ans :
To evaluate the limit lim(x→3) (x + 3), we can simply substitute 3 for x:
lim(x→3) (x + 3) = 3 + 3 = 6
Therefore, the limit of x + 3 as x approaches 3 is 6.
2.
Ans :
To evaluate the limit, we can directly substitute π for x:
lim(x→π) (x – 22/7)
= π – 22/7
Therefore, the limit of (x – 22/7) as x approaches π is π – 22/7.
3.
Ans :
To evaluate the limit, we can simply substitute 1 for r:
lim(r→1) πr^2 = π(1)^2 = π
Therefore, the limit of πr^2 as r approaches 1 is π.
4.
Ans : To evaluate the limit, we can directly substitute 4 for x:
lim(x→4) (4x + 3) / (x – 2) = (4 * 4 + 3) / (4 – 2) = (16 + 3) / 2 = 19 / 2
Therefore, the limit of (4x + 3) / (x – 2) as x approaches 4 is 19/2
5.
Ans : To evaluate the limit, we can’t directly substitute -1 for x because it would result in an indeterminate form of 0/0. Instead, we can try factoring the numerator.
Notice that x^10 + x^5 + 1 can be factored as (x^5 + 1)^2.
So, the limit becomes:
lim(x→-1) [(x^5 + 1)^2 / (x – 1)]
Now, we can use direct substitution:
lim(x→-1) [(x^5 + 1)^2 / (x – 1)] = [(-1)^5 + 1]^2 / (-1 – 1) = 0 / (-2) = 0
Therefore, the limit of (x^10 + x^5 + 1) / (x – 1) as x approaches -1 is 0.
6.
Ans :
7.
Ans :
8.
Ans :
9.
Ans :
lim(x→0) (ax + b) / (cx + 1) = (a(0) + b) / (c(0) + 1) = b / 1 = b
Therefore, the limit of (ax + b) / (cx + 1) as x approaches 0 is b.
10.
Ans :
11.
Ans :
12.
Ans :
13.
Ans :
NCERT Solutions for Class 11 Maths Chapter 12
14.
Ans :
To evaluate the limit, we can use the following trigonometric identity:
lim(x→0) sin(x)/x = 1
We can rewrite the given limit as:
lim(x→0) (sin(ax) / x) / (sin(bx) / x)
Now, using the above identity:
lim(x→0) (sin(ax) / x) / (sin(bx) / x) = (a * 1) / (b * 1) = a/b
Therefore, the limit of sin(ax) / sin(bx) as x approaches 0 is a/b, where a and b are not equal to 0.
15.
Ans :
16.
Ans :
17.
Ans :
18.
Ans :
To evaluate the limit, we can use the following trigonometric identity:
lim(x→0) sin(x)/x = 1
We can rewrite the given limit as:
lim(x→0) (ax + cos(x)) / (b sin(x))
Now, divide both the numerator and denominator by x:
= lim(x→0) ((ax/x) + (cos(x)/x)) / (b sin(x)/x)
Using the trigonometric identity:
= lim(x→0) (a + cos(x)/x) / (b * 1)
As x approaches 0, cos(x)/x approaches 1. Therefore, the limit becomes:
= (a + 1) / b
So, the limit of (ax + cos(x)) / (b sin(x)) as x approaches 0 is (a + 1) / b.
NCERT Solutions for Class 11 Maths Chapter 12
19.
Ans :
20.
Ans :
To evaluate the limit, we can use the following trigonometric identity:
lim(x→0) sin(x)/x = 1
We can rewrite the given limit as:
lim(x→0) (sin(ax) + bx) / (ax + sin(bx))
Now, divide both the numerator and denominator by x:
= lim(x→0) ((sin(ax)/x) + (bx/x)) / ((ax/x) + (sin(bx)/x))
Using the trigonometric identity:
= lim(x→0) ((a * 1) + b) / ((a * 1) + (b * 1))
Simplifying:
= (a + b) / (a + b)
= 1
21.
Ans :
22.
Ans :
23.
Ans :
24.
Ans :
For lim(x→1-) f(x):
Since x is approaching 1 from the left, we use the definition of f(x) for x ≤ 1:
lim(x→1-) f(x) = lim(x→1-) (x^2 – 1)
Direct substitution gives us:
= 1^2 – 1 = 0
For lim(x→1+) f(x):
Since x is approaching 1 from the right, we use the definition of f(x) for x > 1:
lim(x→1+) f(x) = lim(x→1+) (-x^2 – 1)
Direct substitution gives us:
= -(1^2) – 1 = -2
25.
Ans :
For lim(x→0-) f(x):
Since x is approaching 0 from the left, we use the definition of f(x) for x ≠ 0:
lim(x→0-) f(x) = lim(x→0-) |x|/x
For x < 0, |x| = -x. Substituting this:
= lim(x→0-) -x/x = lim(x→0-) -1 = -1
For lim(x→0+) f(x):
Since x is approaching 0 from the right, we use the definition of f(x) for x ≠ 0:
lim(x→0+) f(x) = lim(x→0+) |x|/x
For x > 0, |x| = x. Substituting this:
= lim(x→0+) x/x = lim(x→0+) 1 = 1
26.
Ans :
For lim(x→0-) f(x):
Since x is approaching 0 from the left, we use the definition of f(x) for x ≠ 0:
lim(x→0-) f(x) = lim(x→0-) |x|/x
For x < 0, |x| = -x. Substituting this:
= lim(x→0-) -x/x = lim(x→0-) -1 = -1
For lim(x→0+) f(x):
Since x is approaching 0 from the right, we use the definition of f(x) for x ≠ 0:
lim(x→0+) f(x) = lim(x→0+) |x|/x
For x > 0, |x| = x. Substituting this:
= lim(x→0+) x/x = lim(x→0+) 1 = 1
27.
Ans :
28.
Ans :
Given:
- f(x) = { a + bx, x < 1 { 4, x = 1 { b – ax, x > 1
- lim(x→1) f(x) = f(1) = 4
Solution:
1. Evaluate the limits from both sides:
- Left-hand limit: lim(x→1-) f(x) = lim(x→1-) (a + bx) = a + b
- Right-hand limit: lim(x→1+) f(x) = lim(x→1+) (b – ax) = b – a
2. Apply the condition for the limit to exist:
For the limit to exist, the left-hand limit and the right-hand limit must be equal to the function’s value at x = 1. Therefore:
a + b = 4 (from the left-hand limit) b – a = 4 (from the right-hand limit)
3. Solve the system of equations:
Adding the two equations:
2b = 8 b = 4
Substituting b = 4 into the first equation:
a + 4 = 4
a = 0
NCERT Solutions for Class 11 Maths Chapter 12
29.
Ans :
30.
Ans :
Case 1: a < 0
In this case, as x approaches a, it will also be less than 0. Therefore, we use the definition of f(x) for x < 0:
lim(x→a-) f(x) = lim(x→a-) (|x| + 1)
Since x is approaching a from the left, |x| = -x:
= lim(x→a-) (-x + 1)
Substituting x = a:
= -a + 1
Case 2: a = 0
In this case, the limit is directly the value of f(0):
lim(x→0) f(x) = f(0) = 0
Case 3: a > 0
In this case, as x approaches a, it will also be greater than 0. Therefore, we use the definition of f(x) for x > 0:
lim(x→a+) f(x) = lim(x→a+) (|x| – 1)
= lim(x→a+) (x – 1)
Substituting x = a:
= a – 1
For the limit to exist, the left-hand limit, right-hand limit, and the function’s value at a must all be equal.
-a + 1 = 0 = a – 1
Solving the first equation:
-a + 1 = 0 a = 1
Solving the second equation:
a – 1 = 0 a = 1
Therefore, the limit lim(x→a) f(x) exists only when a = 1.
31.
Ans :
To evaluate the limit lim(x→1) f(x), we can use the given information about the limit of the quotient (f(x) – 2) / (x^2 – 1).
We know that:
lim(x→1) (f(x) – 2) / (x^2 – 1) = π
We can rewrite the expression (x^2 – 1) as (x – 1)(x + 1). Then, the limit becomes:
lim(x→1) (f(x) – 2) / ((x – 1)(x + 1)) = π
Now, we can use the property of limits that states:
lim(x→a) [f(x) / g(x)]
= [lim(x→a) f(x)] / [lim(x→a) g(x)]
Applying this property to our limit:
[lim(x→1) (f(x) – 2)] / [lim(x→1) (x – 1)(x + 1)] = π
Since lim(x→1) (x – 1)(x + 1) = 0, we can multiply both sides of the equation by this expression:
lim(x→1) (f(x) – 2)
= π * 0
lim(x→1) (f(x) – 2) = 0
lim(x→1) f(x) = 2
Therefore, the limit of f(x) as x approaches 1 is 2.
32.
Ans :
Exercise 12.2
1. Find the derivative of x2– 2 at x = 10.
Ans :
To find the derivative of x^2 – 2 at x = 10, we’ll first differentiate the function and then evaluate the derivative at x = 10.
1. Differentiate the function:
f'(x) = d/dx (x^2 – 2) = 2x – 0 = 2x
2. Evaluate the derivative at x = 10:
f'(10) = 2 * 10 = 20
Therefore, the derivative of x^2 – 2 at x = 10 is 20.
2. Find the derivative of x at x = 1
Ans :
The derivative of x at any point is 1.
This is a fundamental rule of calculus. The derivative of a linear function (like x) is its slope, and the slope of the line y = x is 1.
Therefore, the derivative of x at x = 1 is also 1.
3. Find the derivative of 99x at x = l00
Ans :
To find the derivative of 99x at x = 100, we first need to find the general derivative of the function.
The derivative of 99x is 99. This is because the derivative of any linear function ax is a, where a is a constant.
Therefore, the derivative of 99x at x = 100 is also 99
4.
Ans :
(i) f(x) = x^2 – 27
f'(x) = lim(h→0) [(x + h)^2 – 27 – (x^2 – 27)] / h
= lim(h→0) (x^2 + 2hx + h^2 – 27 – x^2 + 27) / h
= lim(h→0) (2hx + h^2) / h
= lim(h→0) (2x + h)
= 2x
Therefore, the derivative of x^2 – 27 is 2x.
(ii) f(x) = (x – 1)(x – 2)
f'(x) = lim(h→0) [(x + h – 1)(x + h – 2) – (x – 1)(x – 2)] / h
= lim(h→0) (x^2 + 2hx + h^2 – 3x + 2 – x^2 + 3x – 2) / h
= lim(h→0) (2hx + h^2) / h
= lim(h→0) (2x + h)
= 2x
Therefore, the derivative of (x – 1)(x – 2) is 2x.
(iii) f(x) = 1/x^2
f'(x) = lim(h→0) [1/(x + h)^2 – 1/x^2] / h
= lim(h→0) [(x^2 – (x + h)^2) / (x^2(x + h)^2)] / h
= lim(h→0) (-2hx – h^2) / (x^2(x + h)^2 * h)
= lim(h→0) (-2x – h) / (x^2(x + h)^2)
= -2x / x^4
= -2/x^3
Therefore, the derivative of 1/x^2 is -2/x^3.
(iv) f(x) = (x + 1)/(x – 1)
f'(x) = lim(h→0) [(x + h + 1)/(x + h – 1) – (x + 1)/(x – 1)] / h
= lim(h→0) [(x + h + 1)(x – 1) – (x + 1)(x + h – 1)] / ((x – 1)(x + h – 1)h)
= lim(h→0) (-2h) / ((x – 1)(x + h – 1)h)
= lim(h→0) -2 / ((x – 1)(x + h – 1))
= -2 / (x – 1)^2
Therefore, the derivative of (x + 1)/(x – 1) is -2 / (x – 1)^2.
NCERT Solutions for Class 11 Maths Chapter 12
5.
Ans :
Given function:
f(x) = x^100/100 + x^99/99 + … + x^2/2 + x + 1
To prove:
f'(1) = 100f'(0)
Solution:
1. Find the derivative of f(x):
f'(x) = x^99 + x^98 + … + x + 1
2. Evaluate f'(1):
f'(1) = 1^99 + 1^98 + … + 1 + 1
= 100
3. Evaluate f'(0):
f'(0) = 0^99 + 0^98 + … + 0 + 1
= 1
4. Compare f'(1) and 100f'(0):
f'(1) = 100
100f'(0) = 100 * 1 = 100
Therefore, f'(1) = 100f'(0).
6.
Ans :
To find the derivative of the given function, we can use the power rule and the sum rule of differentiation.
The power rule states that the derivative of x^n is nx^(n-1), where n is any real number.
The sum rule states that the derivative of the sum of two functions f(x) and g(x) is the sum of their individual derivatives: (f + g)'(x) = f'(x) + g'(x).
d/dx (x^n + ax^(n-1) + a^2x^(n-2) + … + a^(n-1)x + a^n)
= nx^(n-1) + a(n-1)x^(n-2) + a^2(n-2)x^(n-3) + … + a^(n-1) + 0
= nx^(n-1) + a(n-1)x^(n-2) + a^2(n-2)x^(n-3) + … + a^(n-1)
nx^(n-1) + a(n-1)x^(n-2) + a^2(n-2)x^(n-3) + … + a^(n-1)
7.
Ans :
(i) (x – a)(x – b)
Using the product rule:
(uv)’ = u’v + uv’
Let u = x – a
and v = x – b.
Then:
u’ = 1
v’ = 1
So, the derivative of (x – a)(x – b) is:
(x – a)(x – b)’ = (x – a)(1) + (x – b)(1) = 2x – a – b
(ii) (ax^2 + b)^2
Using the chain rule:
(f(g(x)))’ = f'(g(x)) * g'(x)
Let f(u) = u^2
and g(x) = ax^2 + b.
Then:
f'(u) = 2u
g'(x) = 2ax
So, the derivative of (ax^2 + b)^2 is:
(ax^2 + b)^2′ = 2(ax^2 + b) * 2ax = 4ax(ax^2 + b)
(iii) (x – a) / (x – b)
Using the quotient rule:
(u/v)’ = (u’v – uv’) / v^2
Let u = x – a
and v = x – b.
Then:
u’ = 1
v’ = 1
So, the derivative of (x – a) / (x – b) is:
((x – a) / (x – b))’ = ((1)(x – b) – (x – a)(1)) / (x – b)^2
= (x – b – x + a) / (x – b)^2
= (a – b) / (x – b)^2
8.
Ans :
9.
Ans :
(i) 2x^3/4
Using the power rule and the constant multiple rule:
d/dx (2x^3/4) = 2 * (3/4) * x^(3/4 – 1) = 3/2 * x^(-1/4)
(ii) (5x^3 + 3x – 1)(x – 1)
Using the product rule:
(uv)’ = u’v + uv’
Let u = 5x^3 + 3x – 1 and v = x – 1. Then:
u’ = 15x^2 + 3
v’ = 1
So, the derivative is:
(5x^3 + 3x – 1)(x – 1)’ = (15x^2 + 3)(x – 1) + (5x^3 + 3x – 1)(1)
= 15x^3 – 15x^2 + 3x – 3 + 5x^3 + 3x – 1
= 20x^3 – 15x^2 + 6x – 4
(iii) x^-3 (5 + 3x)
Using the product rule:
(uv)’ = u’v + uv’
Let u = x^-3 and v = 5 + 3x. Then:
u’ = -3x^-4
v’ = 3
So, the derivative is:
x^-3 (5 + 3x)’ = (-3x^-4)(5 + 3x) + (x^-3)(3)
= -15x^-4 – 9x^-3 + 3x^-3
= -15x^-4 – 6x^-3
(iv) x^5 (3 – 6x^9)
Using the product rule:
(uv)’ = u’v + uv’
Let u = x^5 and v = 3 – 6x^9. Then:
u’ = 5x^4
v’ = -54x^8
So, the derivative is:
x^5 (3 – 6x^9)’ = (5x^4)(3 – 6x^9) + (x^5)(-54x^8)
= 15x^4 – 30x^13 – 54x^13
= 15x^4 – 84x^13
(v) x^-4 (3 – 4x^5)
Using the product rule:
(uv)’ = u’v + uv’
Let u = x^-4 and v = 3 – 4x^5. Then:
u’ = -4x^-5
v’ = -20x^4
So, the derivative is:
x^-4 (3 – 4x^5)’ = (-4x^-5)(3 – 4x^5) + (x^-4)(-20x^4)
= 16x^-1 – 12x^-5 – 20x^-1
= -4x^-1 – 12x^-5
(vi) 2x^2 / (x + 1)(3x – 1)
Using the quotient rule:
(u/v)’ = (u’v – uv’) / v^2
Let u = 2x^2 and v = (x + 1)(3x – 1). Then:
u’ = 4x
v’ = (1)(3x – 1) + (x + 1)(3) = 6x + 2
So, the derivative is:
(2x^2 / (x + 1)(3x – 1))’ = ((4x)(x + 1)(3x – 1) – (2x^2)(6x + 2)) / ((x + 1)(3x – 1))^2
= (12x^3 – 4x^2 – 4x) / ((x + 1)(3x – 1))^2
10. Find the derivative of cos x from first principle.
Ans :
To find the derivative of cos x from first principles, we need to use the definition of the derivative:
f'(x) = lim(h→0) [f(x + h) – f(x)] / h
For f(x) = cos x, we have:
f'(x) = lim(h→0) [cos(x + h) – cos(x)] / h
Now, we can use the trigonometric identity:
cos(a + b) = cos(a)cos(b) – sin(a)sin(b)
To rewrite the expression:
f'(x) = lim(h→0)
[cos(x)cos(h) – sin(x)sin(h) – cos(x)] / h
Simplifying:
f'(x) = lim(h→0) [cos(x)(cos(h) – 1) – sin(x)sin(h)] / h
Now, we can use the following limits:
- lim(h→0) (cos(h) – 1) / h = 0
- lim(h→0) sin(h) / h = 1
Substituting these limits:
f'(x) = cos(x) * 0 – sin(x) * 1
Therefore, the derivative of cos x is:
f'(x) = -sin(x)
11.
Ans :
(i) sin x cos x
Using the product rule:
(uv)’ = u’v + uv’
Let u = sin x and v = cos x. Then:
u’ = cos x
v’ = -sin x
So, the derivative is:
(sin x cos x)’ = (cos x)(cos x) + (sin x)(-sin x)
= cos^2(x) – sin^2(x)
= cos(2x)
(ii) sec x
Recall that sec x = 1/cos x. Using the quotient rule:
(u/v)’ = (u’v – uv’) / v^2
Let u = 1 and v = cos x. Then:
u’ = 0
v’ = -sin x
So, the derivative is:
(sec x)’ = (0 * cos x – 1 * (-sin x)) / cos^2(x)
= sin x / cos^2(x)
= sec x tan x
(iii) 5 sec x + 4 cos x
Using the sum rule and the results from (ii):
(5 sec x + 4 cos x)’ = 5(sec x)’ + 4(cos x)’
= 5(sec x tan x) – 4sin x
= 5sec x tan x – 4sin x
(iv) cosec x
Recall that cosec x = 1/sin x. Using the quotient rule:
(u/v)’ = (u’v – uv’) / v^2
Let u = 1 and v = sin x. Then:
u’ = 0
v’ = cos x
So, the derivative is:
(cosec x)’ = (0 * sin x – 1 * cos x) / sin^2(x)
= -cos x / sin^2(x)
= -cosec x cot x
(v) 3cot x + 5cosec x
Using the sum rule and the results from (iii) and (iv):
(3cot x + 5cosec x)’ = 3(cot x)’ + 5(cosec x)’
= 3(-csc^2 x) + 5(-cosec x cot x)
= -3csc^2 x – 5cosec x cot x
(vi) 5sin x – 6cos x + 7
Using the sum and difference rules and the derivatives of sin x and cos x:
(5sin x – 6cos x + 7)’ = 5(sin x)’ – 6(cos x)’ + 0
= 5cos x + 6sin x
(vii) 2tan x – 7sec x
Using the sum rule and the derivatives of tan x and sec x:
(2tan x – 7sec x)’ = 2(tan x)’ – 7(sec x)’
= 2sec^2 x – 7sec x tan x
NCERT Solutions for Class 11 Maths Chapter 12
FAQ’s
What is Class 11 Maths Chapter 12 about?
Chapter 12 introduces the basic concepts of Limits and Derivatives, which form the foundation of calculus.
Why are Limits and Derivatives important in Class 11 Maths?
They help students understand how functions behave, change, and approach certain values—skills important for advanced maths and competitive exams.
How do NCERT Solutions help with Chapter 12?
NCERT Solutions give clear, step-by-step explanations that make it easier to understand limits, continuity, and basic derivatives.
What are the key concepts covered in this chapter?
The chapter covers limits, standard limit formulas, derivative rules, and the derivative of simple functions.
Where can I find free solutions for Class 11 Maths Chapter 12?
You can find free, easy-to-understand solutions for Class 11 Maths Chapter 12 – Limits and Derivatives – on trusted educational websites and apps.