Waves

A wave is a disturbance that propagates through a medium, transferring energy from one point to another without net particle displacement.

Two primary wave types exist:

Mechanical Waves:

Require a medium to propagate (e.g., sound waves, water waves, seismic waves)

Can be longitudinal (vibration parallel to the direction of wave propagation) or transverse (vibration perpendicular to the direction of wave propagation)

Electromagnetic Waves:

Do not require a medium to propagate (e.g., light, radio waves, X-rays)

Are always transverse waves

Key Concepts:

Wave Parameters:

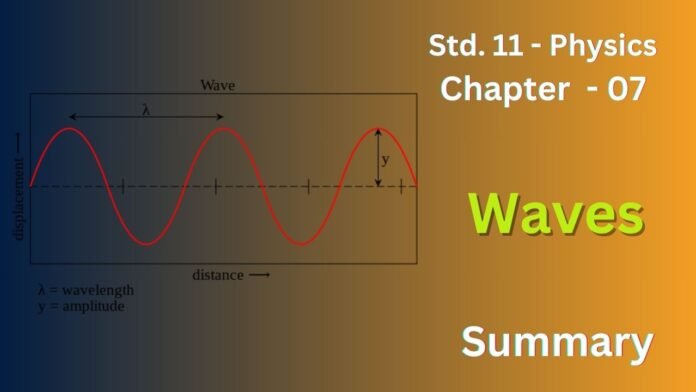
-Wavelength (λ) is the length of one complete cycle of a wave.

– The frequency (ν) equals the number of oscillations divided by the time taken.

– Time Period (T) = Time taken to complete one full oscillation

– Wave Speed (v): Speed at which the wave propagates (v = λν)

Wave Equation:** Relates wave speed, wavelength, and frequency: v = λν

Principle of Superposition: : The net displacement of waves at a point where they meet is the algebraic sum of the individual displacements.

Interference: The superposition of waves can lead to constructive (amplitude increases) or destructive (amplitude decreases) interference.

Standing Waves: Formed by the superposition of two waves of the same frequency and amplitude traveling in opposite directions. They have nodes (points of zero displacement) and antinodes (points of maximum displacement).

Doppler Effect: The apparent change in frequency of a wave due to the relative motion between the source and the observer.

1. A string of mass 2.50 kg is under a tension of 200 N. The length of the stretched string is 20.0 m. If the transverse jerk is struck at one end of the string, how long does the disturbance take to reach the other end?

Ans :Finding the Time Taken for the Disturbance to Reach the Other End

Understanding the Problem:

We have a string with a given mass and length, under tension. A disturbance is created at one end. We need to find the time it takes for this disturbance to reach the other end.

Solution:

1. Calculate the wave speed (v):

Determine speed of a wave on a string by using following formula

v = √(T/μ)

where:

v = wave speed

T =tension in the string (200 N)

μ denotes the linear mass density of the string.

The linear mass density (μ) can be calculated as:

μ = mass/length = 2.5 kg / 20 m = 0.125 kg/m

Substituting the values:

v = √(200 N / 0.125 kg/m) ≈ 40 m/s

2. Calculate the time taken (t):

The time taken for the disturbance to travel the length of the string is given by:

t = distance/speed = length/v

Substituting the values:

t = 20 m / 40 m/s

= 0.5 s

Therefore, the disturbance takes 0.5 seconds to reach the other end of the string.

2. A stone dropped from the top of a tower of height 300 m splashes into the water of a pond near the base of the tower. When is the splash heard at the top given that the speed of sound in air is 340 m s–1 ? (g = 9.8 m s–2)

Ans : To solve this problem, Determine the time elapsed between the two events

Time to hit water:

We can use the equation of motion:

s = ut + (1/2)gt²

Here, s = 300 m (height of the tower), u = 0 (initial velocity), g = 9.8 m/s² (acceleration due to gravity), and t is the time taken.

So, 300 = 0 + (1/2) * 9.8 * t²

Solving for t, we get:

t ≈ 7.82 seconds

Time taken for the sound to travel up:

The speed of sound is 340 m/s, and the distance it needs to travel is 300 m.

So, time taken = distance / speed = 300 / 340 ≈ 0.88 seconds

Therefore, the total time taken for the splash to be heard at the top is:

Total time = Time for stone to fall + Time for sound to travel up

≈ 7.82 + 0.88

≈ 8.7 seconds

So, the splash will be heard approximately 8.7 seconds after the stone is dropped.

3. A steel wire has a length of 12.0 m and a mass of 2.10 kg. What should be the tension in the wire so that speed of a transverse wave on the wire equals the speed of sound in dry air at 20 °C = 343 m s–1 .

Ans : Given:

Length of the string, l = 12.0 m

Total mass of the string, M = 2.10 kg

Wave velocity, v = 343 m/s

The linear mass density of the string, defined as mass per unit length, is

μ = M/l = 2.10/12.0 = 0.175 kg/m

The wave velocity on a string is related to the tension (T) and linear mass density (μ) by the equation:

v = √(T/μ)

Therefore, the tension in the string is:

T = v²μ = (343)² x 0.175 = 2.06 x 10⁴ N.

4. Use the formula to explain why the speed of sound in air

(a) is independent of pressure,

(b) increases with temperature,

(c) increases with humidity.

Ans : Analyzing the Speed of Sound in Air

Understanding the Formula:

Find speed of sound in a medium by using following formula ;

v = √(γP/ρ)

where:

v denote speed of sound

γ denote adiabatic index (ratio of specific heats)

P denote pressure of the medium

ρ denote density of the medium

Now, let’s analyze each part of the question:

a) Independence of Pressure:

If we increase the pressure, the density of the air also increases proportionally.

This is because the number of molecules per unit volume increases with pressure.

As a result, the ratio P/ρ remains constant.

Therefore, the speed of sound, which depends on the square root of this ratio, remains independent of pressure.

b) Increase with Temperature:

As the temperature increases, the average kinetic energy of the air molecules increases.

This leads to an increase in the speed of sound waves as they propagate through the air.

Additionally, the density of air decreases with increasing temperature, which further contributes to an increase in the speed of sound.

c) Increase with Humidity:

Humid air has a higher density than dry air due to the presence of water vapor molecules.

However, the adiabatic index (γ) for moist air is lower than that for dry air.

The combined effect of these factors is that the speed of sound in humid air is slightly higher than in dry air.

In conclusion:

The speed of sound in air is independent of pressure due to the compensating effects of pressure and density changes.

The speed of sound increases with temperature due to increased molecular kinetic energy and decreased density.

The speed of sound increases slightly with humidity due to a lower adiabatic index and increased density.

5. You have learnt that a travelling wave in one dimension is represented by a function y = f (x, t)

where x and t must appear in the combination x – v t or x + v t, i.e. y = f (x ± v t). Is the converse true?

Examine if the following functions for y can possibly represent a travelling wave :

(a) (x – vt ) 2

(b) log [(x + vt)/x0 ]

(c) 1/(x + vt)

Ans : The converse is not necessarily true. A fundamental criterion for a function to describe a traveling wave is that it must have a finite value for all possible values of x and t. None of the given functions for y fulfill this condition. Consequently, none of them can represent a traveling wave.

6. A bat emits ultrasonic sound of frequency 1000 kHz in air. If the sound meets a water surface, what is the wavelength of

(a) the reflected sound,

(b) the transmitted sound?

Speed of sound in air is 340 m s –1 and in water 1486 m s–1 .

Ans : (a) Reflected sound:

The reflected sound travels back through air. So, we use the speed of sound in air to calculate the wavelength.

Given:

(f) denote Frequency

= 1000 kHz

= 1000000 Hz

(v) denote Speed of sound in air

= 340 m/s

Wavelength (λ) = v / f = 340 / 1000000 = 0.00034 m

= 3.4 × 10⁻⁴ m

(b) Transmitted sound:

The transmitted sound travels through water. So, we use the speed of sound in water to calculate the wavelength.

Given:

(f) denote Frequency

= 1000 kHz

= 1000000 Hz

(v) denote Speed of sound in water is

= 1486 m/s

Wavelength (λ) = v / f = 1486 / 1000000 = 0.001486 m

= 1.486 × 10⁻³ m

7. A hospital uses an ultrasonic scanner to locate tumours in a tissue. What is the wavelength of sound in the tissue in which the speed of sound is 1.7 km s–1 ? The operating frequency of the scanner is 4.2 MHz.

Ans : Given:

Speed of sound in tissue (v) = 1.7 km/s = 1700 m/s

Operating frequency (f) = 4.2 MHz = 4.2 x 10^6 Hz

To find: Wavelength (λ)

We can use the formula:

λ = v / f

Substituting the values:

λ = 1700 / (4.2 x 10^6) = 4.0476 x 10^-4 m

Therefore, the wavelength of sound in the tissue is approximately 4.05 x 10^-4 m.

8. A transverse harmonic wave on a string is described by

y(x, t) = 3.0 sin (36 t + 0.018 x + π/4)

where x and y are in cm and t in s. The positive direction of x is from left to right.

(a) Is this a travelling wave or a stationary wave ? If it is travelling, what are the speed and direction of its propagation ?

(b) What are its amplitude and frequency ?

(c) What is the initial phase at the origin ?

(d) What is the least distance between two successive crests in the wave ?

Ans : (a) Travelling Wave:

The given equation, y(x, t) = 3.0 sin(36t + 0.018x + π/4), represents a travelling wave. This is because it involves both spatial (x) and temporal (t) variables, and the wave propagates in a specific direction.

Direction of Propagation:

The positive sign before the coefficient of x indicates that the wave is travelling in the negative x-direction.

Speed of Propagation:

The general equation that describes a travelling wave is:

y(x, t) = A sin(kx – ωt + φ)

Comparing this with the given equation, we can identify:

Angular frequency (ω) = 36 rad/s

Wave number (k) = 0.018 cm⁻¹

The wave speed (v) is related to ω and k by:

v = ω/k

= 36 / 0.018

= 2000 cm/s

= 20 m/s

(b) Amplitude and Frequency:

Amplitude (A): The amplitude is the coefficient of the sine function, which is 3.0 cm.

Frequency (f): The angular frequency (ω) is related to the frequency (f) by ω = 2πf. So, f = ω / 2π = 36 / (2π) ≈ 5.73 Hz.

(c) Initial Phase at the Origin:

The initial phase (φ) is the constant term that is added to the input of the sine function.

In this case, φ = π/4.

(d) Distance Between Successive Crests:

The distance between two successive crests is the wavelength (λ).

The relationship between wavelength and wave number (k) is given by:

λ = 2π / k = 2π / 0.018 ≈ 349 cm

9. For the wave described in Exercise 14.8, plot the displacement (y) versus (t) graphs for x = 0, 2 and 4 cm. What are the shapes of these graphs? In which aspects does the oscillatory motion in travelling wave differ from one point to another: amplitude, frequency or phase ?

Ans : The transverse harmonic wave is described by the equation:

y(x, t) = 3.0 sin(36t + 0.018x + π/4)

For x = 0, the equation becomes:

y(0, t) = 3 sin(36t + π/4)

Here, ω = 36 rad/s, which implies T = 2π/36.

To plot a y versus t graph, we can calculate y values for different values of t using the above equation.

t y

0 3√2/2

T/8 3

2T/8 3√2/2

3T/8 0

4T/8 -3√2/2

5T/8 -3

6T/8 -3√2/2

7T/8 0

T 3√2/2

Export to Sheets

Using these values, we can plot a sinusoidal graph. “Identical graphs are produced for x = 2 cm and x = 4 cm.”

The oscillatory motion in the travelling wave differs only in phase from one point to another. The amplitude and frequency remain constant.

10. For the travelling harmonic wave

y(x, t) = 2.0 cos 2π (10t – 0.0080 x + 0.35)

where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of

(a) 4 m,

(b) 0.5 m,

(c) λ /2,

(d) 3λ /4

Ans : The given wave equation is:

y(x, t)

= 2.0 cos 2π (10t – 0.0080x + 0.35)

Comparing this with the standard wave equation:

y(x, t)

= A cos (kx – ωt + φ)

We can identify:

Wave number (k) = 2π * 0.0080 = 0.016π rad/cm

(ω) denote Angular frequency

= 2π * 10

= 20π rad/s

Phase difference (Δφ) between two points separated by a distance (Δx) is given by:

Δφ = k * Δx

(a) For Δx = 4 m = 400 cm:

Δφ = 0.016π * 400

= 6.4π rad

(b) For Δx

= 0.5 m

= 50 cm:

Δφ

= 0.016π * 50

= 0.8π rad

(c) For Δx = λ/2:

Determine wavelength (λ):

λ = 2π/k = 2π / (0.016π) = 125 cm

So, Δx = λ/2 = 62.5 cm

Δφ = 0.016π * 62.5

= π rad

(d) For Δx = 3λ/4:

Δx = 3 * 125 / 4 = 93.75 cm

Δφ = 0.016π * 93.75

= 1.5π rad

11. The transverse displacement of a string (clamped at its both ends) is given by

where x and y are in m and t in s. The length of the string is 1.5 m and its mass is

3.0 ×10–2 kg.

Answer the following :

(a) Does the function represent a travelling wave or a stationary wave?

(b) Interpret the wave as a superposition of two waves travelling in opposite directions. What is the wavelength, frequency, and speed of each wave ?

(c) Determine the tension in the string.

Ans : (i) Stationary Wave:

The given function, y(x, t) = 0.06 sin(2π/3 x) cos(120πt), represents a stationary wave. This is because it is a product of a sine function of x and a cosine function of t, indicating that the wave pattern doesn’t propagate but oscillates in place.

(ii) Superposition of Two Waves:

A stationary wave can be considered as the superposition of two waves traveling in opposite directions.

Here, equation for such a wave =

y(x, t) = A sin(kx ± ωt)

Comparing this with the given equation, we can identify the two waves as:

Wave 1: y₁(x, t) = 0.03 sin(2π/3 x – 120πt)

Wave 2: y₂(x, t) = 0.03 sin(2π/3 x + 120πt)

“The following information can be derived from these equations:

Wavelength (λ): For both waves, the wave number (k) = 2π/3. Therefore, λ = 2π/k = 3 m.

Frequency (f): For both waves, the angular frequency (ω) = 120π.

Therefore, f = ω/2π = 60 Hz.

Speed of Propagation (v): For both waves, v = λf = 3 m * 60 Hz = 180 m/s.

(iii) Tension in the String:

The speed of a wave on a string is related to its tension (T) and linear mass density (μ) by the equation:

v = √(T/μ)

The linear mass density (μ) is the mass per unit length:

μ = mass/length = (3 x 10⁻² kg) / 1.5 m = 0.02 kg/m

Determine tension (T):

T = μv² = 0.02 kg/m * (180 m/s)² = 648 N

Hence, the tension in the string is 648 N.

12. (i) For the wave on a string described in Exercise 15.11, do all the points on the string oscillate with the same (a) frequency, (b) phase, (c) amplitude?

Explain your answers. (ii) What is the amplitude of a point 0.375 m away from one end?

Ans : (i) For the wave on the string described in questions, we have seen that l = 1.5 m and λ = 3 m. So, it is clear that λ = l/2. For a string clamped at both ends, this is possible only when both ends act as nodes and there is one antinode in the middle. In other words, the entire string vibrates in a single segment.

(a) All string particles, except the nodes, oscillate with the same frequency of 60 Hz.

(b) Since all string particles belong to the same segment, they all oscillate in phase.

(c) Amplitude varies across different particles. The maximum displacement at the antinode is 2A, which equals 0.06 mIt gradually decreases towards the nodes, reaching zero at the nodes themselves.

(ii) To find the amplitude at a point x = 0.375 m, we can substitute cos(120πt) = 1 in the wave equation:

A(x) = 0.06 sin(2π/3 * 0.375) * 1 = 0.06 sin(π/4) = 0.042 m

13. Given below are some functions of x and t to represent the displacement (transverse or longitudinal) of an elastic wave. State which of these represent

(i) a travelling wave,

(ii) a stationary wave or

(iii) none at all:

(a) y = 2 cos (3x) sin (10t)

(b) y = 2x-vt

(c) y = 3 sin (5x – 0.5t) + 4 cos (5x – 0.5t)

(d) y = cos x sin t + cos 2x sin 2t

Ans :(a) The given function corresponds to a stationary wave.

(b) The given function does not conform to the standard form of either a travelling or a stationary wave.

(d) The given function represents the superposition of two independent stationary

14 A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45 Hz. The mass of the wire is 3.5 × 10–2 kg and its linear mass density is 4.0 × 10–2 kg m–1. What is

(a) the speed of a transverse wave on the string, and

(b) the tension in the string?

Ans : Here,

Frequency of vibration (n) = 45 Hz

Mass of the wire (M) = 3.5 x 10^-2 kg

Mass per unit length (m) = 4.0 x 10^-2 kg/m

Therefore, the length of the wire:

l = M/m = (3.5 x 10^-2) / (4.0 x 10^-2) = 7/8 m

As the wire vibrates in its fundamental mode, its length is half a wavelength:

l = λ/2

Therefore, the wavelength (λ) is:

λ = 2l = 2 x (7/8) = 7/4 m = 1.75 m

(a) The speed of the transverse wave (v) is:

v = nλ = 45 x 1.75

= 78.75 m/s

(b) The speed of a wave on a string is related to its tension (T) and linear mass density (m) by the equation:

v = √(T/m)

Squaring both sides and rearranging, we get:

T = v²m = (78.75)² x 4.0 x 10^-2

= 248.06 N

Therefore, the tension in the string is 248.06 N.

15. A metre-long tube open at one end, with a movable piston at the other end, shows resonance with a fixed frequency source (a tuning fork of frequency 340 Hz) when the tube length is 25.5 cm or 79.3 cm. Estimate the speed of sound in air at the temperature of the experiment. The edge effects may be neglected.

Ans :For a tube open at one end, the resonant frequencies are given by:

f_n = n * (v / 4L)

where:

f_n is the nth resonant frequency

n = positive integer (1, 2, 3, …)

v = speed of sound in air

L = length of the tube

In this case, we have two resonant lengths: 25.5 cm and 79.3 cm. Let’s denote them as L1 and L2, respectively.

here,

(n = 1),

f = (v / 4L1)

For the third resonance (n = 3), we have:

f = (3v / 4L2)

Since the frequency f is the same for both resonances, we can equate the two equations:

(v / 4L1) = (3v / 4L2)

Simplifying, we get:

L1 = L2 / 3

Substituting the given values:

25.5 cm = 79.3 cm / 3

This equation holds true, confirming that the given lengths correspond to the first and third harmonics.

Now, we can use either of the resonance conditions to find the speed of sound:

Using the first resonance:

f = (v / 4L1)

Rearranging to solve for v:

v = 4 * f * L1

Substituting the values:

v = 4 * 340 Hz * 0.255 m

≈ 347 m/s

Therefore, the estimated speed of sound in air at the temperature of the experiment is approximately 347 m/s..

16. A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod are given to be 2.53 kHz. What is the speed of sound in steel?

Ans :Here,

(L) denote Length of the rod

= 100 cm

= 1 m

Frequency of vibration (f) = 2.53 kHz = 2.53 x 10^3 Hz

When a rod is clamped at its middle, it forms a node at the center and antinodes at both ends in its fundamental mode of vibration.

As seen in the figure, the length of the rod is equal to half the wavelength:

L = λ/2

Therefore, the wavelength (λ) is:

λ = 2L = 2 x 1 = 2 m

The speed of sound (v) in the rod is given by:

v = fλ

Substituting the values:

v = 2.53 x 10^3 x 2

= 5.06 x 10^3 m/s

Hence, the speed of sound in steel is 5.06 x 10^3 m/s.

17. A pipe 20 cm long is closed at one end. Which harmonic mode of the pipe is resonantly excited by a 430 Hz source ? Will the same source be in resonance with the pipe if both ends are open? (speed of sound in air is 340 m s–1).

Ans :Here,

(l) denote Length of the pipe

= 20 cm

= 0.2 m

(v) denote Frequency of the source

= 430 Hz

(u) denote Speed of sound in air

= 340 m/s

Given,

resonant frequencies for a closed-end pipe,

v = (2n – 1) * (u / 4l)

where,

n = positive integer

(1, 2, 3, …).

Substituting the values:

430 = (2n – 1) * (340 / 4 * 0.2)

Solving for n:

2n – 1 = 1.02

n ≈ 1.01

Since n must be an integer, resonance can only occur for the first (fundamental) mode of vibration.

Given,

resonant frequencies for an open-end pipe,

v = n * (u / 2l)

Substituting the values:

430 = n * (340 / 2 * 0.2)

Solving for n:

n ≈ 0.51

As n must be an integer, resonance cannot occur for the given frequency and pipe length in this case.

18. Two sitar strings A and B playing the note ‘Ga’ are slightly out of tune and produce beats of frequency 6 Hz. The tension in the string A is slightly reduced and the beat frequency is found to reduce to 3 Hz. If the original frequency of A is 324 Hz, what is the frequency of B?

Ans :The superposition of two sound waves with nearly identical frequencies produces the phenomenon of beats.”. The beat frequency is equal to the difference in frequencies of the two waves.

Initially, the beat frequency is 6 Hz, so the frequency of B can be either 330 Hz or 318 Hz.

When the tension in string A is reduced, its frequency will decrease. If the original frequency of B was 330 Hz, reducing the frequency of A would increase the beat frequency, which contradicts the given information.

Therefore, the original frequency of B must have been 318 Hz.

So, the frequency of string B is 318 Hz.

19.Explain why (or how):

(a) in a sound wave, a displacement node is a pressure antinode and vice versa,

(b) bats can ascertain distances, directions, nature, and sizes of the obstacles without any “eyes”,

(c) a violin note and sitar note may have the same frequency, yet we can distinguish between the two notes,

(d) solids can support both longitudinal and transverse waves, but only longitudinal waves can propagate in gases, and

(e) the shape of a pulse gets distorted during propagation in a dispersive medium.

Ans : (a) In a sound wave, a region of minimum displacement (node) corresponds to a region of maximum pressure variation (antinode), and vice versa. This is because pressure variations arise from the compression and rarefaction of the medium due to particle oscillations.

(b) Bats utilize echolocation to navigate their surroundings. They emit high-frequency ultrasonic sound waves that bounce off objects in their path. By analyzing the time delay, intensity, and frequency shift of the returning echoes, bats can accurately determine the distance, direction, size, and texture of obstacles.

(c) The perceived quality or timbre of a sound is influenced by the relative amplitudes of its harmonic components. While a violin and sitar may produce the same fundamental frequency, they differ in their harmonic spectra. This difference in harmonic content allows us to distinguish between the two instruments, even if they are playing the same note.

(d) Solids can support both longitudinal and transverse waves due to their elastic properties, including both shear modulus and bulk modulus. Gases, lacking significant shear strength, can only propagate longitudinal waves, where particles oscillate parallel to the wave’s direction of propagation.

(e) A sound pulse is composed of a range of frequencies. In a dispersive medium, the speed of propagation varies with frequency. This causes different frequency components to travel at different speeds, leading to the spreading and distortion of the pulse over time