NCERT Solutions for Class 6 Maths Chapter 6
Here’s a summary of the Integers chapter from a typical 6th-grade Maths perspective:
Integers:
- Integers are a collection of whole numbers (positive counting numbers like 1, 2, 3, …) and their negatives (numbers less than zero like -1, -2, -3, …).
- Zero (0) is included in the set of integers, but it’s neither positive nor negative.
Representing Integers:
- Integers can be represented on a number line: positive numbers to the right of zero and negative numbers to the left.
- The distance between two points on the number line represents the difference between their values.
Ordering Integers:
- Any positive integer is greater than any negative integer.
- Zero is less than any positive integer and greater than any negative integer.
- When comparing two negative integers, the one with a higher absolute value (distance from zero) is considered larger.
Operations on Integers:
- Addition and subtraction of integers follow similar rules as whole numbers, but you need to consider the signs.
- Positive + Positive = Positive
- Positive + Negative = Depends (result can be positive or negative)
- Negative + Negative = Negative
- Multiplication of integers:
- Positive x Positive = Positive
- Positive x Negative = Negative
- Negative x Negative = Positive
- Division of integers is not always possible because you might not get a whole number result. It’s explored in more advanced math classes.
Applications of Integers:
- Integers are used in many real-world situations, such as representing temperatures (positive for hot, negative for cold), scores (positive for points gained, negative for points deducted), height or depth (positive for above ground, negative for below ground), etc.
Additional points that might be covered:
- Representing integers using algebra symbols like variables (e.g., x, y)
- Identifying even and odd integers (even integers are divisible by 2 without a remainder, odd integers leave a remainder of 1 when divided by 2).
NCERT Solutions for Class 6 Maths Chapter 6
Exercise :
1. Write opposites of the following:
(a) Increase in weight
(b) 30 km North
(c) 326 BC
(d) Loss of ₹700
(e) 100 m above sea level.
Ans :
(a) Increase in weight: Decrease in weight
(b) 30 km North: 30 km South
(c) 326 BC: 326 AD
(d) Loss of ₹700: Gain of ₹700
(e) 100 m above sea level: 100 m below sea level
2. Represent the following numbers as integers with appropriate signs.
(a) An aeroplane is flying at a height two thousand metre above the ground.
(b) A submarine is moving at a depth, eight hundred metre below the sea level.
(c) A deposit of rupees two hundred.
(d) Withdrawal of rupees seven hundred.
Ans :
(a) Aeroplane: +2000 meters
(b) Submarine: -800 meters
(c) Deposit: +200 rupees
(d) Withdrawal: -700 rupees
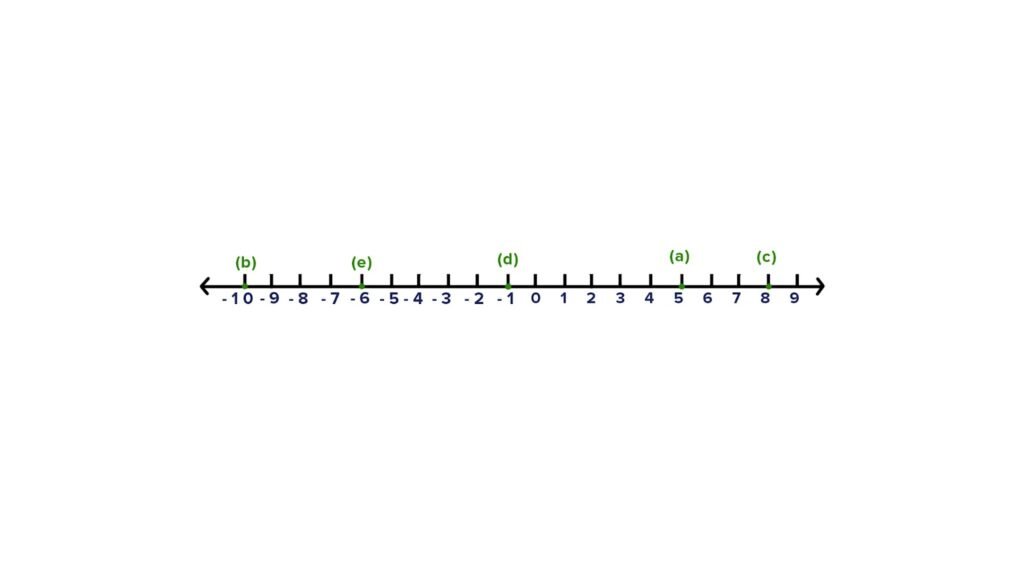
3. Represent the following numbers on a number line: ,
(a) +5
(b) -10
(c) ±8
(d) -1
(e) -6
Ans :
4. Adjacent figure is a vertical number line, representing integers. Observe it and locate the following points:
(a) If point D is +8, then which point is -8?
(b) Is point G a negative integer or a positive integer?
(c) Write integers for points B and E.
(d) Which point marked on this number line has the least value?
(e) Arrange all the points in decreasing order of value.
Ans :
(a) F represents -8
(b) G is a negative integer.
(c) B represents +4 and E represents – 10
(d) E has the least value of -10.
(e) Decreasing order of all the points are: D, C, B, A, 0, H, G, F and E.
5. Following is the list of temperatures of five places in India on a particular day of the year.
| Place | Temperature |
| Siachin | 10°C below 0°C |
| Shimla | 2°C below 0°C |
| Ahmedabad | 30°C above 0°C |
| Delhi | 20°C above 0°C |
| Srinagar | 5°C above 0°C |
(a) Write the temperatures of these places in the form of integers in the blank column.
(b) Following is the number line representing the temperature in degree Celsius.
(c) Which is the coolest place?
(d) Write the names of the places where temperatures are above 10°C.
Ans :
(a)
| Place | Temperature | In the form of integers |
| Siachin | 10°C below 0°C | -10°C |
| Shimla | 2°C below 0°C | -2°C |
| Ahmedabad | 30°C above 0°C | +30°C |
| Delhi | 20°C above 0°C | +20°C |
| Srinagar | 5°C above 0°C | +5°C |
(b) Siachin – -10
Shimla – -2
Ahmedabad – 30
Delhi – 20
Srinagar – 5
(c) Siachin 2°C
(d) Ahmedabad 30°C
Delhi 20°C
6. In each of the following pairs, which number is to the right of the other on the number line?
(a) 2, 9
(b) -3, -8
(c) 0, -1
(d) -11, 10
(e) -6, 6
(f) 1, -100
Ans :
(a) 2, 9: 9 is to the right of 2. (Positive numbers increase as you move to the right)
(b) -3, -8: -3 is to the right of -8. (Negative numbers decrease as you move to the right)
(c) 0, -1: 0 is to the right of -1. (Positive zero is greater than any negative number) (d) -11, 10: 10 is to the right of -11. (Positive numbers are greater than negative numbers)
(e) -6, 6: 6 is to the right of -6. (Positive numbers are greater than negative numbers) (f) 1, -100: 1 is to the right of -100. (Positive numbers are greater than negative numbers)
7. Write all the integers between the given pairs (write them in the increasing order):
(a) 0 and -7
(b) -4 and 4
(c) -8 and -15
(d) -30 and -23
Ans :
(a) 0 and -7: Integers between 0 and -7 are: – 6, – 5, – 4, -3,-2,- 1.
(b) -4 and 4: The integers in increasing order are: -4, -3, -2, -1, 0, 1, 2, 3, 4
(c) -8 and -15: The integers in increasing order are: -8, -7, -6, -5, -4, -3, -2, -1, -10, -9, -11, -12, -13, -14, -15
(d) -30 and -23: The integers in increasing order are: -30, -29, -28, -27, -26, -25, -24, -23
8. (a) Write four negative integers greater than -20.
(b) Write four negative integers less than – 10.
Ans :
(a) Four negative integers greater than -20:
- -19
- -18
- -17
- -16
(b) Four negative integers less than -10:
- -11
- -12
- -13
- -14
9. For the following statements, write True (T) or False (F).
If the statement is false, correct the statement.
(a) – 8 is to the right of – 10 on a number line.
(b) – 100 is to the right of- 50 on a number line.
(c) Smallest negative integer is – 1
(d) – 26 is greater than – 25.
Ans :
(a) False (F). Correction: -8 is to the right of -10 on a number line. (Positive numbers move to the right, and negative numbers decrease as you move to the right.)
(b) False (F). Correction: -100 is to the left of -50 on a number line. (As you move to the right on the number line, negative numbers become less negative.)
(c) False (F). Correction: There is no smallest negative integer. Negative integers go on forever in the direction of negative infinity.
(d) False (F). Correction: -26 is less than -25. (Negative numbers decrease in value as you move to the right on the number line.)
10. Draw a number line and answer the following:
(a) Which number will we reach if we move 4 numbers to the right of -2.
(b) Which number will we reach if we move 5 numbers to the left of 1.
(c) If we are at -8 on the number line, in which direction should we move to reach -13?
(d) If we are at -6 on the number line, in which direction should we move to reach -1?
Ans :
(a) Move 4 steps to the right from -2. You will land on +2.
(b) Move 5 steps to the left from 1. You will land on -4.
(c) You need to move to the left because -13 is further to the left (more negative) than -8.
(d) You need to move to the left because -1 is further to the left (more negative) than -6.
NCERT Solutions for Class 6 Maths Chapter 6
Exercise 6.2
1. Using the number line write the integer which is:
(a) 3 more than 5
(b) 5 more than -5
(c) 6 less than 2
Ans :
(a) 3 more than 5:
- Find 5 on the number line.
- Since “more than” means adding, move 3 steps to the right from 5.
- You will land on 8.
Therefore, 3 more than 5 is 8.
(b) 5 more than -5:
- Find -5 on the number line.
- Since “more than” means adding, move 5 steps to the right from -5.
- You will land on 0.
Therefore, 5 more than -5 is 0.
(c) 6 less than 2:
- Find 2 on the number line.
- Since “less than” means subtracting, move 6 steps to the left from 2.
- You will land on -4.
Therefore, 6 less than 2 is -4.
2. Use number line and add the following integers:
(a) 9 + (-6)
(b) 5 + (-11)
(c) (-1) + (-7)
(d) (- 5) + 10
(e) (-1) + (-2) + (-3)
Ans :
(a) 9 + (-6):
- Start at 9 on the number line.
- Since adding a negative number is the same as subtracting, move 6 steps to the left from 9.
- You will land on 3.
Therefore, 9 + (-6) = 3.
(b) 5 + (-11):
- Start at 5 on the number line.
- Move 11 steps to the left from 5.
- You will land on -6.
Therefore, 5 + (-11) = -6.
(c) (-1) + (-7):
- Start at -1 on the number line.
- Move 7 steps to the left from -1.
- You will land on -8.
Therefore, (-1) + (-7) = -8.
(d) (-5) + 10:
- Start at -5 on the number line.
- Since adding a positive number means moving to the right, move 10 steps to the right from -5.
- You will land on 5.
Therefore, (-5) + 10 = 5.
(e) (-1) + (-2) + (-3):
- Imagine starting at 0 on the number line.
- Move 1 step to the left from 0 to reach -1.
- Then, move another 2 steps to the left from -1 to reach -3.
- Finally, move another 1 step to the left from -3 to reach -4.
4. Add without using number line:
(а) 11 + (-7)
(b) (-13) + (+18)
(c) (-10) + (+19)
(d) (-250) + (+150)
(e) (-380) + (-270)
(f) (-217) + (-100)
Ans :
(a) 11 + (-7):
- Positive + Negative = Depends on the signs.
- In this case, 11 (positive) is larger than 7 (negative).
- So, we subtract the negative number from the positive number: 11 – 7 = 4.
(b) (-13) + (+18):
- Negative + Positive = Depends on the signs.
- Here, 18 (positive) is larger than 13 (negative).
- So, we subtract the negative number from the positive number: -13 + 18 = 5.
(c) (-10) + (+19):
- Similar to (b), Negative + Positive = Depends on the signs.
- 19 (positive) is larger than 10 (negative).
- So, -10 + 19 = 9.
(d) (-250) + (+150):
- Follow the same rule. Negative + Positive = Depends on the signs.
- Here, 150 (positive) is smaller than 250 (negative).
- Absolute value of -250 is larger than 150, so the result will be negative.
- We subtract the smaller number (positive in this case) from the larger number (negative): -250 + 150 = -100.
(e) (-380) + (-270):
- Both numbers are negative. Negative + Negative = Negative.
- Add the absolute values of -380 and -270: |-380| + |-270| = 380 + 270 = 650.
- Since both numbers were negative, the result is also negative: -380 + (-270) = -650.
(f) (-217) + (-100):
- Similar to (e), Negative + Negative = Negative.
- Add the absolute values: |-217| + |-100| = 217 + 100 = 317.
- Since both numbers were negative, the result is negative: -217 + (-100) = -317.
4. Find the sum of:
(a) 137 and -354
(b) -52 and 52 .
(d) -312, 39 and 192
(d) -50, -200 and 300
Ans :
(a) 137 and -354:
- Positive + Negative = Depends on the signs.
- Here, the absolute value of -354 (negative) is larger than 137 (positive).
- So, the sum will be negative: 137 + (-354) = -217.
(b) -52 and 52:
- Negative + Positive = Depends on the signs.
- Since both numbers have the same absolute value, but opposite signs, their sum will be zero.
- -52 + 52 = 0.
(c) -312, 39 and 192:
- This can be solved in multiple ways:
- Method 1: Add two numbers at a time
- Add the positive numbers: 39 + 192 = 231
- Add the result to the negative number: -312 + 231 = -81.
- Method 2: Group positive and negative numbers
- Combine the positive numbers: 39 + 192 = 231
- Add the combined positive value to the negative number: -312 + 231 = -81.
- Method 1: Add two numbers at a time
(d) -50, -200 and 300:
- Consider positive and negative values separately.
- Add the positive number: 300
- Add the negative numbers together: -50 – 200 = -250
- Combine the positive and negative sums: 300 – 250 = 50.
5. Find the sum of:
(a) (- 7) + (-9) + 4 + 16
(b) (37) + (-2) + (-65) + (-18)
Ans :
(a) (-7) + (-9) + 4 + 16
We can group the positive and negative numbers for easier addition:
- Positive numbers: 4 + 16 = 20
- Negative numbers: -7 – 9 = -16
Now, add the positive and negative sums: 20 (positive) – 16 (negative) = 4.
Therefore, the sum is 4.
(b) (37) + (-2) + (-65) + (-18)
Similar grouping:
- Positive number: 37
- Negative numbers: -2 – 65 – 18 = -85
Add the positive and negative sums: 37 (positive) – 85 (negative) = -48.
Therefore, the sum is -48.
NCERT Solutions for Class 6 Maths Chapter 6
Exercise 6.3
1. Find:
(a) 35 – (20)
(b) 72 – (90)
(c) (-15) – (-18)
(d) (- 20) – (13)
(e) 23 – (-12)
(f) (-32) – (-40)
Ans :
(a) 35 – (20): 35 minus 20 equals 15.
(b) 72 – (90): 72 minus 90 equals -18 (since subtracting a larger number results in a negative difference).
(c) (-15) – (-18): This is a subtraction of negative numbers. Treat it like adding a positive number. -15 plus 3 (which is the opposite of -18) equals 3.
(d) (-20) – (13): Subtracting another negative number from -20 makes it more negative. -20 minus 13 equals -33.
(e) 23 – (-12): 23 plus 12 (opposite of -12) equals 35.
(f) (-32) – (-40): Subtracting a larger negative number from -32 makes it more positive. -32 plus 8 (opposite of -40) equals 8.
2. Fill in the blanks with >, < or = sign.
(a) (-3) + (-6) ______ (-3) – (-6)
(b) (-21) – (-10) ______ (- 31) + (-11)
(c) 45 – (-11) ______ 57 + (-4)
(d) (-25) – (-42) ______ (-42) – (-25)
Ans :
(a) (-3) + (-6) < (-3) – (-6)
(b) (-21) – (-10) > (- 31) + (-11)
(c) 45 – (-11) > 57 + (-4)
(d) (-25) – (-42) = (-42) – (-25)
3. Fill in the blanks.
(a) (-8) + …. = 0
(b) 13 + …. = 0
(c) 12 + (-12) = ….
(d) (-4) + …. = – 12
(e) …. -15 = – 10.
Ans :
(a) (-8) + 8 = 0
Since adding a number to its opposite (negative) results in zero, 8 is the opposite (additive inverse) of -8.
(b) 13 + (-13) = 0
Similar to (a), -13 is the opposite of 13.
(c) 12 + (-12) = 0
Following the pattern, -12 is the opposite of 12.
(d) (-4) + 8 = -12
To find the missing number, we can add 4 to both sides of the equation:
4. Find :
(a) (-7) – 8 – (-25)
(b) (-13) + 32 – 8 – 1
(c) (-7) + (-8) + (-90)
(d) 50 – (-40) – (-2)
Ans :
(a) (-7) – 8 + 25 = 10.
(b) (-13) + 32 – 8 – 1 = 19 – 8 – 1 = 10
(c) -7 – 8 – 90 = -105.
(d) 50 + 40 + 2 = 92.
FAQ’s
What topics are covered in NCERT Class 6 Maths Chapter 6?
The chapter covers fundamental concepts of integers, including their introduction, representation on a number line, addition, subtraction, multiplication, and division of integers.
How can NCERT Solutions for Class 6 Maths Chapter 6 help me understand integers better?
NCERT Solutions provide detailed explanations and step-by-step solutions to problems, making it easier for students to grasp the concepts of integers and perform calculations accurately.
Are there any real-life applications of integers discussed in this chapter?
Yes, NCERT Class 6 Maths Chapter 6 discusses real-life situations where integers are used, such as in banking transactions, temperature calculations, and elevation measurements.
What is the significance of understanding integers in mathematics?
Integers play a crucial role in various mathematical operations and real-life scenarios. Understanding integers helps in solving mathematical problems accurately and interpreting numerical data effectively.
How can I practice and reinforce my understanding of integers after studying Chapter 6?
After studying Chapter 6, you can practice exercises from the textbook, solve additional problems from reference books, and use online resources for further practice. Additionally, discussing concepts with peers and seeking guidance from teachers can enhance your understanding of integers.


