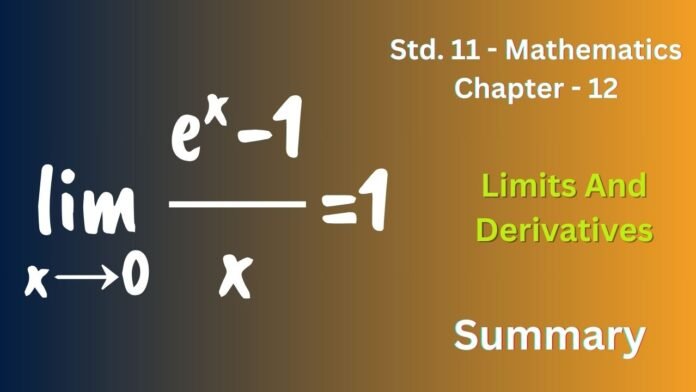Chapter 12.1: Introduction
- Limits: The concept of a limit is central to calculus and is used to describe the behavior of a function as its input approaches a certain value.
- Derivatives: Derivatives measure the rate of change of a function. They are essential for understanding concepts like velocity, acceleration, and slopes of curves.
Chapter 12.2: Limits of Functions
- Definition of Limit: The limit of a function f(x) as x approaches a is denoted by lim(x→a) f(x). It represents the value that f(x) approaches as x gets closer and closer to a.
- Left-hand and Right-hand Limits: These are limits taken from the left and right sides of a point, respectively.
- Existence of Limits: For a limit to exist, the left-hand and right-hand limits must be equal.
- Limit Laws: These are rules for evaluating limits of algebraic combinations of functions.
Chapter 12.3: Evaluation of Limits
- Methods of Evaluation: Direct substitution, factorization, rationalization, and using standard limits.
- Standard Limits: Important limits such as lim(x→0) sin(x)/x = 1 and lim(x→0) (1 – cos(x))/x = 0.
Chapter 12.4: Derivative
- Notation: f'(a) or dy/dx.
- Geometric Interpretation: The derivative at a point represents the slope of the tangent line to the graph of f(x) at that point.
Chapter 12.5: Differentiation
- Rules of Differentiation: Power rule, sum rule, difference rule, product rule, quotient rule, chain rule.
- Differentiation of Trigonometric Functions: Derivatives of sin(x), cos(x), tan(x), cot(x), sec(x), and csc(x).
Key Concepts:
- Limits and their evaluation
- Derivatives and their geometric interpretation
- Rules of differentiation
- Applications of derivatives (e.g., finding velocity, acceleration, tangent lines)
Exercise 12.1
Evaluate the following limits in Exercises 1 to 22.
1.
Ans :
To evaluate the limit lim(x→3) (x + 3), we can simply substitute 3 for x:
lim(x→3) (x + 3) = 3 + 3 = 6
Therefore, the limit of x + 3 as x approaches 3 is 6.
2.
Ans :
To evaluate the limit, we can directly substitute π for x:
lim(x→π) (x – 22/7)
= π – 22/7
Therefore, the limit of (x – 22/7) as x approaches π is π – 22/7.
3.
Ans :
To evaluate the limit, we can simply substitute 1 for r:
lim(r→1) πr^2 = π(1)^2 = π
Therefore, the limit of πr^2 as r approaches 1 is π.
4.
Ans : To evaluate the limit, we can directly substitute 4 for x:
lim(x→4) (4x + 3) / (x – 2) = (4 * 4 + 3) / (4 – 2) = (16 + 3) / 2 = 19 / 2
Therefore, the limit of (4x + 3) / (x – 2) as x approaches 4 is 19/2
5.
Ans : To evaluate the limit, we can’t directly substitute -1 for x because it would result in an indeterminate form of 0/0. Instead, we can try factoring the numerator.
Notice that x^10 + x^5 + 1 can be factored as (x^5 + 1)^2.
So, the limit becomes:
lim(x→-1) [(x^5 + 1)^2 / (x – 1)]
Now, we can use direct substitution:
lim(x→-1) [(x^5 + 1)^2 / (x – 1)] = [(-1)^5 + 1]^2 / (-1 – 1) = 0 / (-2) = 0
Therefore, the limit of (x^10 + x^5 + 1) / (x – 1) as x approaches -1 is 0.
6.
Ans :
7.
Ans :
8.
Ans :
9.
Ans :
lim(x→0) (ax + b) / (cx + 1) = (a(0) + b) / (c(0) + 1) = b / 1 = b
Therefore, the limit of (ax + b) / (cx + 1) as x approaches 0 is b.
10.
Ans :
11.
Ans :
12.
Ans :
13.
Ans :
14.
Ans :
To evaluate the limit, we can use the following trigonometric identity:
lim(x→0) sin(x)/x = 1
We can rewrite the given limit as:
lim(x→0) (sin(ax) / x) / (sin(bx) / x)
Now, using the above identity:
lim(x→0) (sin(ax) / x) / (sin(bx) / x) = (a * 1) / (b * 1) = a/b
Therefore, the limit of sin(ax) / sin(bx) as x approaches 0 is a/b, where a and b are not equal to 0.
15.
Ans :
16.
Ans :
17.
Ans :
18.
Ans :
To evaluate the limit, we can use the following trigonometric identity:
lim(x→0) sin(x)/x = 1
We can rewrite the given limit as:
lim(x→0) (ax + cos(x)) / (b sin(x))
Now, divide both the numerator and denominator by x:
= lim(x→0) ((ax/x) + (cos(x)/x)) / (b sin(x)/x)
Using the trigonometric identity:
= lim(x→0) (a + cos(x)/x) / (b * 1)
As x approaches 0, cos(x)/x approaches 1. Therefore, the limit becomes:
= (a + 1) / b
So, the limit of (ax + cos(x)) / (b sin(x)) as x approaches 0 is (a + 1) / b.
19.
Ans :
20.
Ans :
To evaluate the limit, we can use the following trigonometric identity:
lim(x→0) sin(x)/x = 1
We can rewrite the given limit as:
lim(x→0) (sin(ax) + bx) / (ax + sin(bx))
Now, divide both the numerator and denominator by x:
= lim(x→0) ((sin(ax)/x) + (bx/x)) / ((ax/x) + (sin(bx)/x))
Using the trigonometric identity:
= lim(x→0) ((a * 1) + b) / ((a * 1) + (b * 1))
Simplifying:
= (a + b) / (a + b)
= 1
21.
Ans :
22.
Ans :
23.
Ans :
24.
Ans :
For lim(x→1-) f(x):
Since x is approaching 1 from the left, we use the definition of f(x) for x ≤ 1:
lim(x→1-) f(x) = lim(x→1-) (x^2 – 1)
Direct substitution gives us:
= 1^2 – 1 = 0
For lim(x→1+) f(x):
Since x is approaching 1 from the right, we use the definition of f(x) for x > 1:
lim(x→1+) f(x) = lim(x→1+) (-x^2 – 1)
Direct substitution gives us:
= -(1^2) – 1 = -2
25.
Ans :
For lim(x→0-) f(x):
Since x is approaching 0 from the left, we use the definition of f(x) for x ≠ 0:
lim(x→0-) f(x) = lim(x→0-) |x|/x
For x < 0, |x| = -x. Substituting this:
= lim(x→0-) -x/x = lim(x→0-) -1 = -1
For lim(x→0+) f(x):
Since x is approaching 0 from the right, we use the definition of f(x) for x ≠ 0:
lim(x→0+) f(x) = lim(x→0+) |x|/x
For x > 0, |x| = x. Substituting this:
= lim(x→0+) x/x = lim(x→0+) 1 = 1
26.
Ans :
For lim(x→0-) f(x):
Since x is approaching 0 from the left, we use the definition of f(x) for x ≠ 0:
lim(x→0-) f(x) = lim(x→0-) |x|/x
For x < 0, |x| = -x. Substituting this:
= lim(x→0-) -x/x = lim(x→0-) -1 = -1
For lim(x→0+) f(x):
Since x is approaching 0 from the right, we use the definition of f(x) for x ≠ 0:
lim(x→0+) f(x) = lim(x→0+) |x|/x
For x > 0, |x| = x. Substituting this:
= lim(x→0+) x/x = lim(x→0+) 1 = 1
27.
Ans :
28.
Ans :
Given:
- f(x) = { a + bx, x < 1 { 4, x = 1 { b – ax, x > 1
- lim(x→1) f(x) = f(1) = 4
Solution:
1. Evaluate the limits from both sides:
- Left-hand limit: lim(x→1-) f(x) = lim(x→1-) (a + bx) = a + b
- Right-hand limit: lim(x→1+) f(x) = lim(x→1+) (b – ax) = b – a
2. Apply the condition for the limit to exist:
For the limit to exist, the left-hand limit and the right-hand limit must be equal to the function’s value at x = 1. Therefore:
a + b = 4 (from the left-hand limit) b – a = 4 (from the right-hand limit)
3. Solve the system of equations:
Adding the two equations:
2b = 8 b = 4
Substituting b = 4 into the first equation:
a + 4 = 4
a = 0
29.
Ans :
30.
Ans :
Case 1: a < 0
In this case, as x approaches a, it will also be less than 0. Therefore, we use the definition of f(x) for x < 0:
lim(x→a-) f(x) = lim(x→a-) (|x| + 1)
Since x is approaching a from the left, |x| = -x:
= lim(x→a-) (-x + 1)
Substituting x = a:
= -a + 1
Case 2: a = 0
In this case, the limit is directly the value of f(0):
lim(x→0) f(x) = f(0) = 0
Case 3: a > 0
In this case, as x approaches a, it will also be greater than 0. Therefore, we use the definition of f(x) for x > 0:
lim(x→a+) f(x) = lim(x→a+) (|x| – 1)
= lim(x→a+) (x – 1)
Substituting x = a:
= a – 1
For the limit to exist, the left-hand limit, right-hand limit, and the function’s value at a must all be equal.
-a + 1 = 0 = a – 1
Solving the first equation:
-a + 1 = 0 a = 1
Solving the second equation:
a – 1 = 0 a = 1
Therefore, the limit lim(x→a) f(x) exists only when a = 1.
31.
Ans :
To evaluate the limit lim(x→1) f(x), we can use the given information about the limit of the quotient (f(x) – 2) / (x^2 – 1).
We know that:
lim(x→1) (f(x) – 2) / (x^2 – 1) = π
We can rewrite the expression (x^2 – 1) as (x – 1)(x + 1). Then, the limit becomes:
lim(x→1) (f(x) – 2) / ((x – 1)(x + 1)) = π
Now, we can use the property of limits that states:
lim(x→a) [f(x) / g(x)]
= [lim(x→a) f(x)] / [lim(x→a) g(x)]
Applying this property to our limit:
[lim(x→1) (f(x) – 2)] / [lim(x→1) (x – 1)(x + 1)] = π
Since lim(x→1) (x – 1)(x + 1) = 0, we can multiply both sides of the equation by this expression:
lim(x→1) (f(x) – 2)
= π * 0
lim(x→1) (f(x) – 2) = 0
lim(x→1) f(x) = 2
Therefore, the limit of f(x) as x approaches 1 is 2.
32.
Ans :
Exercise 12.2
1. Find the derivative of x2– 2 at x = 10.
Ans :
To find the derivative of x^2 – 2 at x = 10, we’ll first differentiate the function and then evaluate the derivative at x = 10.
1. Differentiate the function:
f'(x) = d/dx (x^2 – 2) = 2x – 0 = 2x
2. Evaluate the derivative at x = 10:
f'(10) = 2 * 10 = 20
Therefore, the derivative of x^2 – 2 at x = 10 is 20.
2. Find the derivative of x at x = 1
Ans :
The derivative of x at any point is 1.
This is a fundamental rule of calculus. The derivative of a linear function (like x) is its slope, and the slope of the line y = x is 1.
Therefore, the derivative of x at x = 1 is also 1.
3. Find the derivative of 99x at x = l00
Ans :
To find the derivative of 99x at x = 100, we first need to find the general derivative of the function.
The derivative of 99x is 99. This is because the derivative of any linear function ax is a, where a is a constant.
Therefore, the derivative of 99x at x = 100 is also 99
4.
Ans :
(i) f(x) = x^2 – 27
f'(x) = lim(h→0) [(x + h)^2 – 27 – (x^2 – 27)] / h
= lim(h→0) (x^2 + 2hx + h^2 – 27 – x^2 + 27) / h
= lim(h→0) (2hx + h^2) / h
= lim(h→0) (2x + h)
= 2x
Therefore, the derivative of x^2 – 27 is 2x.
(ii) f(x) = (x – 1)(x – 2)
f'(x) = lim(h→0) [(x + h – 1)(x + h – 2) – (x – 1)(x – 2)] / h
= lim(h→0) (x^2 + 2hx + h^2 – 3x + 2 – x^2 + 3x – 2) / h
= lim(h→0) (2hx + h^2) / h
= lim(h→0) (2x + h)
= 2x
Therefore, the derivative of (x – 1)(x – 2) is 2x.
(iii) f(x) = 1/x^2
f'(x) = lim(h→0) [1/(x + h)^2 – 1/x^2] / h
= lim(h→0) [(x^2 – (x + h)^2) / (x^2(x + h)^2)] / h
= lim(h→0) (-2hx – h^2) / (x^2(x + h)^2 * h)
= lim(h→0) (-2x – h) / (x^2(x + h)^2)
= -2x / x^4
= -2/x^3
Therefore, the derivative of 1/x^2 is -2/x^3.
(iv) f(x) = (x + 1)/(x – 1)
f'(x) = lim(h→0) [(x + h + 1)/(x + h – 1) – (x + 1)/(x – 1)] / h
= lim(h→0) [(x + h + 1)(x – 1) – (x + 1)(x + h – 1)] / ((x – 1)(x + h – 1)h)
= lim(h→0) (-2h) / ((x – 1)(x + h – 1)h)
= lim(h→0) -2 / ((x – 1)(x + h – 1))
= -2 / (x – 1)^2
Therefore, the derivative of (x + 1)/(x – 1) is -2 / (x – 1)^2.
5.
Ans :
Given function:
f(x) = x^100/100 + x^99/99 + … + x^2/2 + x + 1
To prove:
f'(1) = 100f'(0)
Solution:
1. Find the derivative of f(x):
f'(x) = x^99 + x^98 + … + x + 1
2. Evaluate f'(1):
f'(1) = 1^99 + 1^98 + … + 1 + 1
= 100
3. Evaluate f'(0):
f'(0) = 0^99 + 0^98 + … + 0 + 1
= 1
4. Compare f'(1) and 100f'(0):
f'(1) = 100
100f'(0) = 100 * 1 = 100
Therefore, f'(1) = 100f'(0).
6.
Ans :
To find the derivative of the given function, we can use the power rule and the sum rule of differentiation.
The power rule states that the derivative of x^n is nx^(n-1), where n is any real number.
The sum rule states that the derivative of the sum of two functions f(x) and g(x) is the sum of their individual derivatives: (f + g)'(x) = f'(x) + g'(x).
d/dx (x^n + ax^(n-1) + a^2x^(n-2) + … + a^(n-1)x + a^n)
= nx^(n-1) + a(n-1)x^(n-2) + a^2(n-2)x^(n-3) + … + a^(n-1) + 0
= nx^(n-1) + a(n-1)x^(n-2) + a^2(n-2)x^(n-3) + … + a^(n-1)
nx^(n-1) + a(n-1)x^(n-2) + a^2(n-2)x^(n-3) + … + a^(n-1)
7.
Ans :
(i) (x – a)(x – b)
Using the product rule:
(uv)’ = u’v + uv’
Let u = x – a
and v = x – b.
Then:
u’ = 1
v’ = 1
So, the derivative of (x – a)(x – b) is:
(x – a)(x – b)’ = (x – a)(1) + (x – b)(1) = 2x – a – b
(ii) (ax^2 + b)^2
Using the chain rule:
(f(g(x)))’ = f'(g(x)) * g'(x)
Let f(u) = u^2
and g(x) = ax^2 + b.
Then:
f'(u) = 2u
g'(x) = 2ax
So, the derivative of (ax^2 + b)^2 is:
(ax^2 + b)^2′ = 2(ax^2 + b) * 2ax = 4ax(ax^2 + b)
(iii) (x – a) / (x – b)
Using the quotient rule:
(u/v)’ = (u’v – uv’) / v^2
Let u = x – a
and v = x – b.
Then:
u’ = 1
v’ = 1
So, the derivative of (x – a) / (x – b) is:
((x – a) / (x – b))’ = ((1)(x – b) – (x – a)(1)) / (x – b)^2
= (x – b – x + a) / (x – b)^2
= (a – b) / (x – b)^2
8.
Ans :
9.
Ans :
(i) 2x^3/4
Using the power rule and the constant multiple rule:
d/dx (2x^3/4) = 2 * (3/4) * x^(3/4 – 1) = 3/2 * x^(-1/4)
(ii) (5x^3 + 3x – 1)(x – 1)
Using the product rule:
(uv)’ = u’v + uv’
Let u = 5x^3 + 3x – 1 and v = x – 1. Then:
u’ = 15x^2 + 3
v’ = 1
So, the derivative is:
(5x^3 + 3x – 1)(x – 1)’ = (15x^2 + 3)(x – 1) + (5x^3 + 3x – 1)(1)
= 15x^3 – 15x^2 + 3x – 3 + 5x^3 + 3x – 1
= 20x^3 – 15x^2 + 6x – 4
(iii) x^-3 (5 + 3x)
Using the product rule:
(uv)’ = u’v + uv’
Let u = x^-3 and v = 5 + 3x. Then:
u’ = -3x^-4
v’ = 3
So, the derivative is:
x^-3 (5 + 3x)’ = (-3x^-4)(5 + 3x) + (x^-3)(3)
= -15x^-4 – 9x^-3 + 3x^-3
= -15x^-4 – 6x^-3
(iv) x^5 (3 – 6x^9)
Using the product rule:
(uv)’ = u’v + uv’
Let u = x^5 and v = 3 – 6x^9. Then:
u’ = 5x^4
v’ = -54x^8
So, the derivative is:
x^5 (3 – 6x^9)’ = (5x^4)(3 – 6x^9) + (x^5)(-54x^8)
= 15x^4 – 30x^13 – 54x^13
= 15x^4 – 84x^13
(v) x^-4 (3 – 4x^5)
Using the product rule:
(uv)’ = u’v + uv’
Let u = x^-4 and v = 3 – 4x^5. Then:
u’ = -4x^-5
v’ = -20x^4
So, the derivative is:
x^-4 (3 – 4x^5)’ = (-4x^-5)(3 – 4x^5) + (x^-4)(-20x^4)
= 16x^-1 – 12x^-5 – 20x^-1
= -4x^-1 – 12x^-5
(vi) 2x^2 / (x + 1)(3x – 1)
Using the quotient rule:
(u/v)’ = (u’v – uv’) / v^2
Let u = 2x^2 and v = (x + 1)(3x – 1). Then:
u’ = 4x
v’ = (1)(3x – 1) + (x + 1)(3) = 6x + 2
So, the derivative is:
(2x^2 / (x + 1)(3x – 1))’ = ((4x)(x + 1)(3x – 1) – (2x^2)(6x + 2)) / ((x + 1)(3x – 1))^2
= (12x^3 – 4x^2 – 4x) / ((x + 1)(3x – 1))^2
10. Find the derivative of cos x from first principle.
Ans :
To find the derivative of cos x from first principles, we need to use the definition of the derivative:
f'(x) = lim(h→0) [f(x + h) – f(x)] / h
For f(x) = cos x, we have:
f'(x) = lim(h→0) [cos(x + h) – cos(x)] / h
Now, we can use the trigonometric identity:
cos(a + b) = cos(a)cos(b) – sin(a)sin(b)
To rewrite the expression:
f'(x) = lim(h→0)
[cos(x)cos(h) – sin(x)sin(h) – cos(x)] / h
Simplifying:
f'(x) = lim(h→0) [cos(x)(cos(h) – 1) – sin(x)sin(h)] / h
Now, we can use the following limits:
- lim(h→0) (cos(h) – 1) / h = 0
- lim(h→0) sin(h) / h = 1
Substituting these limits:
f'(x) = cos(x) * 0 – sin(x) * 1
Therefore, the derivative of cos x is:
f'(x) = -sin(x)
11.
Ans :
(i) sin x cos x
Using the product rule:
(uv)’ = u’v + uv’
Let u = sin x and v = cos x. Then:
u’ = cos x
v’ = -sin x
So, the derivative is:
(sin x cos x)’ = (cos x)(cos x) + (sin x)(-sin x)
= cos^2(x) – sin^2(x)
= cos(2x)
(ii) sec x
Recall that sec x = 1/cos x. Using the quotient rule:
(u/v)’ = (u’v – uv’) / v^2
Let u = 1 and v = cos x. Then:
u’ = 0
v’ = -sin x
So, the derivative is:
(sec x)’ = (0 * cos x – 1 * (-sin x)) / cos^2(x)
= sin x / cos^2(x)
= sec x tan x
(iii) 5 sec x + 4 cos x
Using the sum rule and the results from (ii):
(5 sec x + 4 cos x)’ = 5(sec x)’ + 4(cos x)’
= 5(sec x tan x) – 4sin x
= 5sec x tan x – 4sin x
(iv) cosec x
Recall that cosec x = 1/sin x. Using the quotient rule:
(u/v)’ = (u’v – uv’) / v^2
Let u = 1 and v = sin x. Then:
u’ = 0
v’ = cos x
So, the derivative is:
(cosec x)’ = (0 * sin x – 1 * cos x) / sin^2(x)
= -cos x / sin^2(x)
= -cosec x cot x
(v) 3cot x + 5cosec x
Using the sum rule and the results from (iii) and (iv):
(3cot x + 5cosec x)’ = 3(cot x)’ + 5(cosec x)’
= 3(-csc^2 x) + 5(-cosec x cot x)
= -3csc^2 x – 5cosec x cot x
(vi) 5sin x – 6cos x + 7
Using the sum and difference rules and the derivatives of sin x and cos x:
(5sin x – 6cos x + 7)’ = 5(sin x)’ – 6(cos x)’ + 0
= 5cos x + 6sin x
(vii) 2tan x – 7sec x
Using the sum rule and the derivatives of tan x and sec x:
(2tan x – 7sec x)’ = 2(tan x)’ – 7(sec x)’
= 2sec^2 x – 7sec x tan x