The chapter begins by defining Force as an external agent capable of changing a body’s state of rest or motion, or its size and shape. It introduces the concept of Inertia, which is the inherent property of an object to resist changes in its state of motion. Inertia is directly proportional to mass: the greater the mass, the greater the inertia. The chapter then establishes Newton’s First Law of Motion (the Law of Inertia), stating that a body remains at rest or in uniform motion unless acted upon by a net external force. This law naturally leads to the classification of forces into unbalanced forces (which cause acceleration) and balanced forces (which result in zero net force and no change in motion).
Next, the summary delves into Newton’s Second Law of Motion, which quantitatively relates force to motion. It first defines momentum (p) as the product of mass and velocity . The Second Law then states that the net external force acting on a body is directly proportional to the rate of change of its momentum. For a constant mass, this simplifies to the famous formula: (Force equals mass times acceleration). This is the key equation for solving dynamics problems. The chapter also briefly covers the unit of force, the Newton (N), and its relationship to mass and acceleration.
Finally, the chapter covers Newton’s Third Law of Motion, which is the principle of action and reaction. This law states that for every action force, there is an equal and opposite reaction force. Crucially, the action and reaction forces always act on two different bodies. This explains how systems like walking, swimming, and rocket propulsion work. The concepts are often illustrated with practical examples like the recoil of a gun and forces on interacting blocks, solidifying the idea that forces always occur in pairs.
Exercise 3 (A)
Question 1.
(a) Explain giving two examples of following : Contact forces
(b) Explain giving two examples of following : Non – contact forces
Ans:
(a) Contact Forces
Contact forces are those forces that arise only when two interacting objects are physically touching each other.
- Frictional Force (or Friction): This force always opposes motion when one surface slides or tends to slide over another. It acts tangentially along the surfaces in contact.
- Example 1: When you push a book across a table, the opposing force that slows the book down is friction between the book’s cover and the tabletop.
- Example 2: The force applied by brakes on a bicycle wheel to stop it is a frictional force.
- Normal Reaction Force: This is the perpendicular push exerted by a surface on an object resting on it. It prevents the object from falling through the surface.
- Example 1: A book resting on a shelf exerts a downward gravitational force, and the shelf exerts an equal and opposite upward normal force on the book.
- Example 2: The upward force of a floor supporting a person standing on it.
(b) Non-Contact Forces (Field Forces)
Non-contact forces are those forces that act on an object without any physical contact between the interacting bodies. These forces act through the space surrounding the object, often referred to as a field.
- Gravitational Force: This is the force of attraction that exists between any two masses. Its strength depends on the mass of the objects and the distance between them.
- Example 1: A ball thrown up falls back down to Earth due to the gravitational pull.
- Example 2: The Earth revolving around the Sun is held in its orbit by the Sun’s gravitational force.
- Magnetic Force: This is the force exerted by magnets on other magnets or on ferromagnetic materials like iron.
- Example 1: A magnet attracting a nail from a short distance without touching it.
- Example 2: The force of repulsion between the two poles (North-North or South-South) of two separate magnets.
Question 2.
Classify the following amongst contact and non – contact forces:
Frictional force
Normal reaction force
Force of tension in a string
Gravitational force
Electrostatic force
Magnetic force
Ans:
| Force | Classification | Explanation |
| Frictional force | Contact | Arises from the direct physical interaction (rubbing) between two surfaces. |
| Normal reaction force | Contact | Is the supporting force exerted by a surface perpendicular to the object touching it. |
| Force of tension in a string | Contact | Is the pulling force transmitted through a string, rope, or cable, requiring physical connection. |
| Gravitational force | Non-Contact | Acts remotely through a field, attracting any two objects with mass. |
| Electrostatic force | Non-Contact | Acts remotely between two charged particles or objects. |
| Magnetic force | Non-Contact | Acts remotely through a field, exerted by magnets on magnetic materials or moving charges. |
Question 3.
Give one example in each case where :
The force is of contact, and Force is at a distance
Ans:
| Type of Force | Example | Explanation |
| Contact Force | Pushing a shopping cart | The force you apply requires direct physical contact with the cart to initiate or change its motion. |
| Non-Contact Force | A magnet pulling an iron nail | The magnetic force acts through the surrounding space (a field) to attract the nail without touching it. |
Question 4.
(a) A ball is hanging by string from the ceiling of the roof. Draw a neat labelled diagram showing the forces acting on the ball and the string.
(b) A spring is compressed against a rigid wall. Draw a neat and labeled diagram showing the forces acting on the spring.
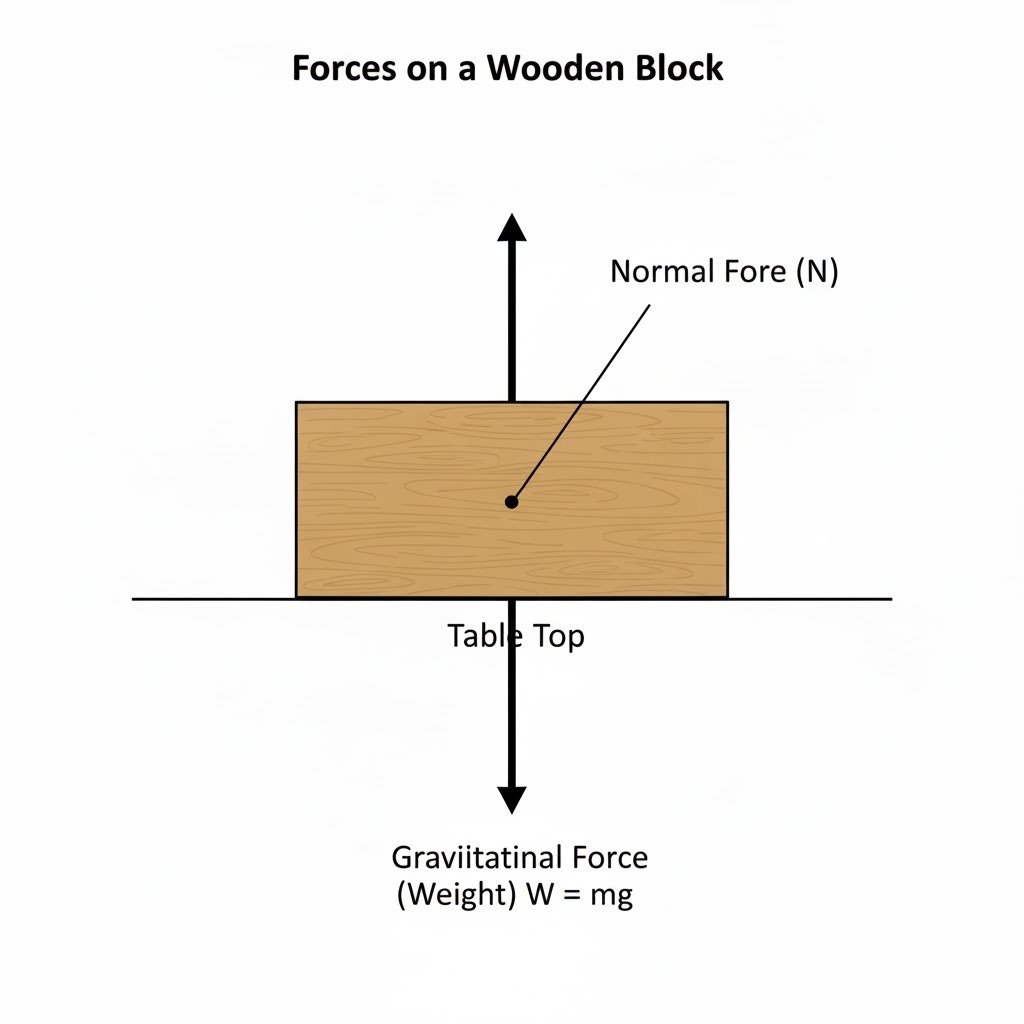
(c) A wooden block is placed on a table top. Name the forces acting on the block and draw a neat and labelled diagram to show the point of application and direction of these forces.
Ans:
(a)
Here’s the diagram showing the forces acting on the ball:
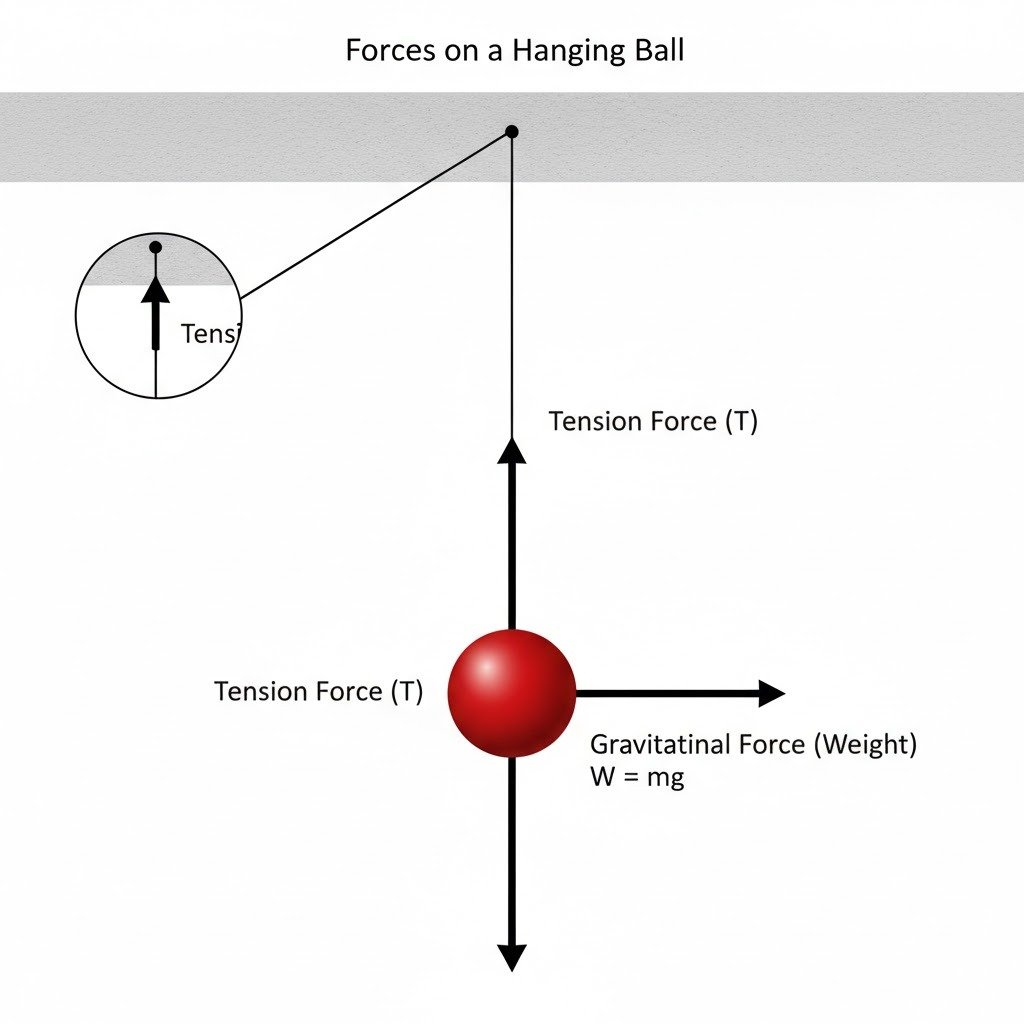
The forces acting on the ball are:
- Gravitational Force (Weight – W): Acts downwards, originating from the center of mass of the ball.
- Tension Force (T): Acts upwards along the string, exerted by the string on the ball.
(b) Spring compressed against a rigid wall:
Here’s the diagram illustrating the forces acting on the spring:
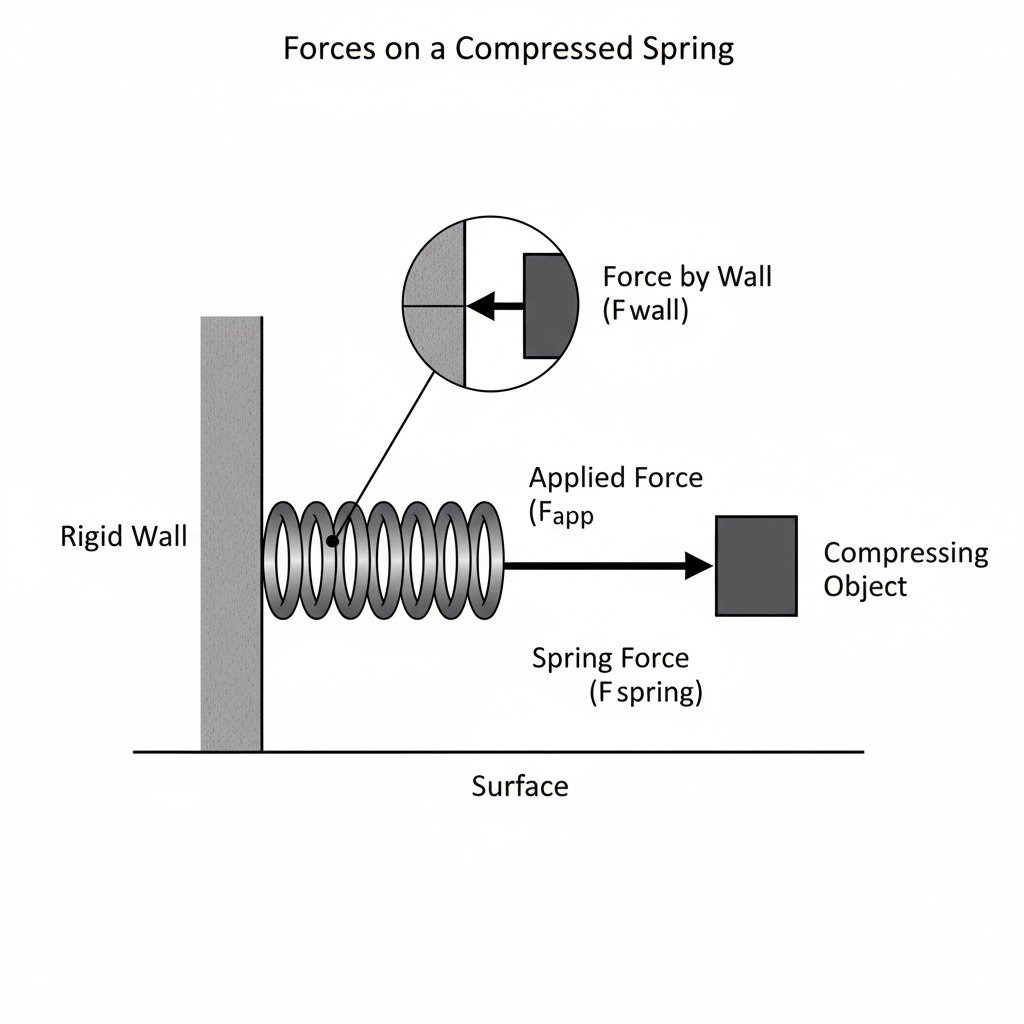
The forces acting on the spring are:
- Applied Force (F_app): The force compressing the spring from one end (e.g., from your hand or another object). This acts into the spring.
- Force by Wall (F_wall): The force exerted by the rigid wall on the spring, pushing it outwards (Newton’s third law to the spring’s push on the wall). This acts out of the spring, opposite to the direction of compression.
- Spring Force (F_spring): The internal restorative force of the spring itself, acting to return it to its original length. When compressed, this force acts outwards from both ends.
(c) Wooden block on a table top:
The forces acting on the block are:
- Gravitational Force (Weight): The force exerted by the Earth on the block, pulling it downwards.
- Normal Force: The force exerted by the table top on the block, perpendicular to the surface and pushing upwards.
Here’s the diagram showing the point of application and direction of these forces:
Question 5.
State one factor on which the magnitude of a non-contact force depends. How does it depend on the factor stated by you?
Ans:
Factor: The separation distance between the objects.
Dependence: The strength of the force weakens as the distance between the objects grows larger.
Explanation:
This inverse relationship is a fundamental principle for forces like gravity and electromagnetism. A more precise way to state it is that the force is inversely proportional to the square of the distance separating the objects. This is often called the inverse-square law.
In simpler terms, if you change the distance, the force changes by the square of that change.
Mathematical relationship: Force F ∝ 1d 2, where d is the distance. Practical example: Imagine the force between two magnets. When they are very close, the pull is strong. If you move them to three times their original separation, the force isn’t just three times weaker; it becomes nine times weaker (because32=9 ).
Question 6.
The separation between two masses is reduced to half. How is the magnitude of gravitational force between them affected?
Ans:
The nature of this dependence is that the force weakens as the distance increases. For fundamental forces like gravity and electromagnetism, this relationship is precisely defined by an inverse-square law. This means the strength of the force is inversely proportional to the square of the distance between the objects’ centers.
To illustrate, consider the gravitational force between two masses. If the separation between them is halved, the force does not merely double; it becomes four times stronger. This quadrupling occurs because the value of the distance in the denominator is squared. Halving the distance means the denominator becomes one-fourth of its original value, which results in the overall force value being multiplied by four.
Question 7.
State the effects of a force applied on A non-rigid, and A rigid body.
How does the effect of the force differ in the two cases?
Ans:
The application of a force produces different effects depending on whether the body is rigid or non-rigid.
Effects of a Force
1. On a Rigid Body
A rigid body is an idealized body where the distance between any two of its particles remains constant regardless of the force applied.
The effects of a force on a rigid body are limited to changing its state of motion:
- Change in Motion (Translation): The force can start motion in a stationary body, stop a moving body, or change the speed or direction of a moving body.
- Change in Orientation (Rotation): If the force is applied away from the center of mass (or center of rotation), it can cause the body to rotate or turn (known as the moment of force or torque).
- No Deformation: The force cannot change the size or shape of an ideal rigid body.
2. On a Non-Rigid Body
A non-rigid body (or deformable body) can change its inter-particle spacing and, therefore, its shape and size when a force is applied.
The effects of a force on a non-rigid body include both changes in motion and changes in form:
- Change in Motion (Translation/Rotation): Similar to a rigid body, the force can change the state of rest or motion (speed, direction, or rotation) of the body.
- Change in Form (Deformation): The force can change the size, shape, or volume of the body. This is the characteristic effect that defines a non-rigid body (e.g., compressing a sponge or stretching a rubber band).
How the Effect of the Force Differs
The primary difference in the effect of a force on the two types of bodies is the occurrence of deformation:
| Feature | Rigid Body (e.g., a solid steel block) | Non-Rigid Body (e.g., a clay ball) |
| Motion | Force causes change in motion (translation or rotation). | Force causes change in motion (translation or rotation). |
| Form/Shape | Force does NOT cause deformation (no change in shape or size). | Force DOES cause deformation (change in shape or size). |
| Summary | Force only produces external effects (changes in motion). | Force produces both external effects (motion) and internal effects (deformation). |
The key takeaway is that an applied force will always cause deformation in a non-rigid body along with any possible motion, whereas it will only cause motion (translation or rotation) in a rigid body.
Question 8.
Give one example in each of the following cases where a force:
(i) Stops a moving body.
(ii) Moves a stationary body.
(iii) Changes the size of a body.
(iv) Changes the shape of a body.
Ans:
| Case | Example |
| (i) Stops a moving body. | A fielder in a cricket match applies a force with their hands to stop a moving ball. |
| (ii) Moves a stationary body. | Kicking a stationary football applies a force that causes it to move. |
| (iii) Changes the size of a body. | Pushing the plunger of a syringe filled with air or water applies a force that compresses the contents, thereby changing the volume (size) of the trapped fluid/gas. |
| (iv) Changes the shape of a body. | Squeezing a piece of soft clay applies a force that changes its shape. (e.g., molding clay). |
Exercise 3 (A)
Question 1.
Which of the following is a contact force:
- Electrostatic force
- Gravitational force
- Frictional force
- Magnetic force
Question 2.
The non – contact force is :
- Force of reaction
- Force due to gravity
- Tension in string
- Force of friction
Exercise 3 (B)
Question 1.
Name the physical quantity that causes motion in a body.
Ans:
The physical quantity responsible for initiating or altering the state of motion of a body is Force.
Specifically, a net external force (or unbalanced force) is the agent that produces a change in motion. The effects of this force are described by the following:
- Starting Motion: A body at rest requires an unbalanced force to begin moving.
- Changing Speed: A moving body will speed up or slow down if an unbalanced force acts upon it along the direction of motion.
- Changing Direction: A moving body requires an unbalanced force to change the direction of its motion.
As established by Newton’s Second Law of Motion, the net force Facting on an object is directly proportional to the rate of change of its linear momentum.For an object with constant mass m, this relationship simplifies to:
F= ma
Here, a represents the acceleration of the body.Since acceleration is the rate at which velocity changes, force is fundamentally the cause of any change in the velocity (magnitude or direction) of an object.
Question 2.
Is force needed to keep a moving body in motion?
Ans:
This is the central concept of Newton’s First Law of Motion, often called the Law of Inertia.
Explanation
- Inertia: A body’s natural tendency (or inertia) is to maintain its current state of motion. If it’s at rest, it stays at rest; if it’s moving, it continues to move at a constant velocity (constant speed and constant direction).
- Net Force is Zero: According to the First Law, a body moving with a constant velocity has a net external force of zero acting upon it. The net force is the vector sum of all forces.
- Force Causes Change: Force is only required to change the state of motion—to accelerate the body (speed up, slow down, or change direction).
Everyday Observation vs. Physics
In daily life, it seems like a continuous force is needed (e.g., you must keep pedaling a bicycle or running a car engine). However, this is because of opposing forces like:
- Friction: The force between surfaces (like tires on the road).
- Air Resistance (Drag): The force from air molecules.
To maintain a constant velocity on Earth, you must apply a force equal and opposite to these opposing forces. This applied force simply balances the friction and drag, resulting in a net force of zero, which then allows the object to move without acceleration (i.e., at a constant velocity). If you were in the vacuum of deep space, a single initial push would be enough to keep a body moving forever without any additional force.
Question 3.
A ball moving on a table top eventually stops. Explain the reason .
Ans:
The fundamental reason a moving ball on a tabletop eventually stops is the presence of unbalanced external forces that oppose its motion, overcoming its inertia.
According to Newton’s First Law of Motion (the Law of Inertia), an object in motion will remain in motion with a constant velocity unless acted upon by a net external force. Since the ball’s velocity changes (it slows down and stops), a net retarding force must be at work.
The primary forces responsible for stopping the ball are:
1. Force of Friction (Rolling Resistance)
This is the main reason the ball slows down and stops.
- Mechanism: Friction acts between the surface of the ball and the surface of the tabletop.
- Energy Conversion: This force causes the kinetic energy (energy of motion) of the ball to be continuously converted into thermal energy (heat) and some sound energy, leading to a decrease in the ball’s speed until all the initial kinetic energy is dissipated and the ball comes to rest.
- Rolling Resistance: The friction that resists rolling motion arises largely from the slight, unavoidable deformation of the ball and the surface at the point of contact. This deformation creates a resistive torque that opposes the rolling motion.
2. Air Resistance (Drag)
This is a secondary force that also contributes to slowing the ball down.
- Mechanism: The ball has to push through the air (or any surrounding fluid medium) as it moves. The air molecules exert a force, called drag, on the ball in the direction opposite to its motion.
- Magnitude: While always present, this effect is typically much smaller than the friction between the ball and the table, especially at low speeds.
Question 4.
A ball is moving on a perfectly smooth horizontal surface. If no force is applied on it, then will its speed decrease, increase or remain unchanged?
Ans:
Here is the explanation:
- Perfectly Smooth Horizontal Surface: This means there is no frictional force acting horizontally on the ball. Frictional force is typically the main force that opposes motion and causes a moving object to slow down (decrease its speed).
- No Force is Applied: This means the net external force Fnet acting on the ball is zero. While gravity acts downward and the normal force from the surface acts upward, these forces are balanced and cancel each other out, leaving a zero net force in both the vertical and horizontal directions.
- Newton’s First Law: This law states that an object in motion will remain in motion with the same speed and in the same direction unless acted upon by an unbalanced external force.
Since Fnet = 0, the ball has zero acceleration a= Fnet m = 0
Therefore, the ball will continue to move at a constant velocity (constant speed and constant direction), and its speed will remain unchanged.
Question 5.
What is Galileo’s law of inertia?
Ans:
Galileo’s law of inertia is a fundamental principle in classical mechanics that describes the natural tendency of an object to resist changes in its state of motion. It served as the crucial conceptual foundation for what later became Isaac Newton’s First Law of Motion.
Galileo’s law states that:
A body moving on a perfectly level surface will continue in the same direction at a constant speed unless it is disturbed by an external force.
Context and Explanation
Prior to Galileo, the prevailing Aristotelian view held that an external force was required to maintain motion. Galileo challenged this by reasoning based on his experiments with inclined planes:
- Inclined Plane Experiment: Galileo observed that a ball rolling down an incline and up a second incline would reach nearly the same height, regardless of the angle of the second incline (neglecting friction).
- Ideal Horizontal Plane: He then reasoned that if the second incline were made perfectly horizontal (a “level surface”) and there were absolutely no friction or air resistance, the ball would never reach the original height and, therefore, would have to continue rolling indefinitely at a constant velocity.
This thought experiment led him to conclude that a force is not necessary to keep a body moving, but rather is necessary only to change its state of motion (i.e., to start it, stop it, or change its direction). This tendency of a body to maintain its state of rest or uniform motion is called inertia.
The concept of inertia established by Galileo is often summarized in the following two parts, which are essentially the statements of Newton’s First Law:
- An object at rest will remain at rest.
- An object in uniform motion (constant speed in a straight line) will remain in uniform motion.
- …unless acted upon by an unbalanced external force.
Question 6.
State Newton’s first law of motion.
Ans:
Newton’s first law of motion, the Law of Inertia, fundamentally describes the natural tendency of an object to resist changes to its motion.
Here is a unique restatement of the law:
An object possesses an inherent characteristic, called inertia, that dictates its behavior in the absence of external influence: Any mass maintains its state of zero motion (rest) or constant, straight-line velocity unless an unbalanced force is imposed upon it.
Key Implications
The essence of this law can be broken down into two distinct scenarios:
- Objects at Rest: To move a stationary object, a net force is absolutely required to overcome its inertia of rest. In the absence of such a push or pull, the object remains perpetually immobile.
- Objects in Motion: A moving object, once set into uniform motion (steady speed in an unwavering direction), requires a net force to slow it down, speed it up, or curve its path. Without external forces like friction or air resistance, the object would continue its journey at that same constant velocity indefinitely.
Question 7.
State and explain the law of inertia (or Newton’s first law of motion).
Ans:
The Law of Inertia is also known as Newton’s First Law of Motion.
Here is the statement and a brief explanation:
Statement of the Law of Inertia
A body at rest will remain at rest, and a body in uniform motion will remain in uniform motion along a straight line, unless acted upon by an unbalanced external force.
Explanation of the Law
This law essentially defines the property of inertia, which is the natural tendency of an object to resist changes in its state of motion.
- If the Net Force is Zero: If a body has no net external force acting on it , it will maintain its current velocity:
- If velocity v is zero (at rest), it stays at rest.
- If velocity v is constant (uniform motion), it continues at that constant velocity.
- To Change Motion: A force is required only to change the state of motion (i.e., to cause acceleration). In the absence of force (like gravity, friction, air resistance, etc.), an object would simply continue moving forever in a straight line at a constant speed.
Question 8.
What is meant by the term inertia?
Ans:
The term inertia refers to the inherent property of an object to resist changes in its state of motion (or state of rest).
In simpler terms:
- If an object is at rest, inertia is its tendency to stay at rest.
- If an object is in motion, inertia is its tendency to keep moving at the same velocity (same speed and same direction).
The mass of an object is the quantitative measure of its inertia: the greater the mass, the greater the inertia.
Question 9.
Give a qualitative definition of force on the basis of Newton’s first law of motion.
Ans:
Based on Newton’s first law of motion, force is defined as a push or a pull that is necessary to change the state of motion or state of rest of a body.
In other words, since an object maintains its state of uniform motion or rest unless acted upon by an external agent, a force is that external influence or cause which is required to initiate a change in its velocity (i.e., cause acceleration).
Question 10.
Name the factor on which the inertia of a body depends and state how it depends on the factor stated by you .
Ans:
The factor on which the inertia of a body depends is its mass m.
It depends on the mass in a directly proportional manner:
- How it depends: The greater the mass of a body, the greater its inertia.
- Conversely: The smaller the mass of a body, the smaller its inertia.
Inertia is fundamentally the measure of a body’s resistance to any change in its state of motion (i.e., its resistance to acceleration), and mass is the quantitative measure of this inertia.
Question 11.
Give two examples to show that greater the mass, greater is the inertia of the body.
Ans:
Inertia is a body’s natural tendency to resist any change in its state of motion. Mass is the quantitative measure of that inertia. Therefore, a greater mass implies a greater resistance to a change in motion.
Here are two examples demonstrating this relationship:
1. Pushing a Vehicle vs. Pushing a Bicycle
- Scenario: Imagine attempting to push a parked truck (high mass) and a parked bicycle (low mass) from a state of rest.
- Observation: You must exert a significantly greater force to get the heavy truck moving compared to the bicycle.
- Conclusion: The truck’s greater mass gives it greater inertia (greater resistance to starting motion), requiring a larger force to change its state of rest.
2. Catching a Stone vs. Catching a Rubber Ball
- Scenario: Consider a stone and a rubber ball of the same size, both thrown at the same speed. You attempt to catch both.
- Observation: The stone (higher density, therefore higher mass) is much harder to stop than the rubber ball (lower mass), and it exerts a greater impact force on your hands.
- Conclusion: The stone’s greater mass gives it greater inertia (greater resistance to stopping motion), requiring a larger force over a given time to bring it to rest.
Question 12.
‘More the mass, the more difficult it is to move the body from rest’. Explain this statement by giving an example.
Ans:
The statement “More the mass, the more difficult it is to move the body from rest” is a straightforward description of a physical property called inertia.
Explanation based on Inertia
Inertia is the inherent property of a body that resists any change in its state of rest or motion. Mass is the quantitative measure of a body’s inertia.
- Higher Mass Greater Inertia: A body with greater mass possesses greater inertia. This means it has a stronger tendency to remain at rest (if stationary) or to continue moving (if in motion).
- Difficulty in Motion: To overcome this greater inertia and change the body’s state from rest to motion, a larger force must be applied, making it “more difficult” to move.
Example
Consider trying to push two stationary objects:
- A small, empty cardboard box with low mass.
- A large, fully loaded truck of high mass.
You can easily set the cardboard box into motion with a gentle tap (small force). However, getting the large, loaded truck to even budge requires a significantly greater force.
This is because the loaded truck has far greater mass and thus greater inertia, offering much more resistance to the change in its state of rest compared to the light cardboard box.
Question 13.
Name the two kinds of inertia.
Ans:
The two kinds of inertia are:
- Inertia of Rest
- Inertia of Motion
Question 14.
Give one example of each of the following :
(a) inertia of rest, and (b) inertia of motion .
Ans:
Examples of Inertia
Inertia is the natural tendency of an object to resist a change in its state of motion.
(a) Inertia of Rest
This is the tendency of a body to remain at rest and resist being set into motion.
- Example: When a stationary bus suddenly starts moving, passengers standing inside tend to fall backwards. This happens because their feet (in contact with the bus floor) move forward, but their upper body resists this change due to inertia and tries to stay in its original state of rest.
(b) Inertia of Motion
This is the tendency of a body to remain in uniform motion (constant speed and direction) and resist being stopped or slowed down.
- Example: When a fast-moving car or bus suddenly applies brakes, the passengers tend to fall forward. This is because the lower part of their body stops with the vehicle, but their upper body continues to move forward due to its inertia of motion.
Question 15.
Two equal and opposite forces act on a stationary body. Will the body move? Give a reason to your answer.
Ans:
No, the body will not move.
Reason
When two equal and opposite forces act on a stationary body, they constitute a balanced pair of forces.
- Net Force is Zero: The forces cancel each other out, resulting in a net force (resultant force) of zero.
- Newton’s First Law: According to Newton’s First Law of Motion (the Law of Inertia), a stationary body remains at rest unless acted upon by an unbalanced external force.
Question 16.
Two equal and opposite forces act on a moving object. How is its motion affected? Give a reason.
Ans:
The motion of the object is unaffected; it will continue to move at a constant velocity (same speed and same direction).
Reason
The two forces are equal in magnitude and opposite in direction, meaning they are balanced forces.
When forces are balanced, the net force (Fnet) acting on the object is zero (Fnet = 0).
According to Newton’s First Law of Motion (The Law of Inertia), an object in motion will continue in motion with a constant velocity unless acted upon by a nonzero net force. Since the net force is zero, the object’s velocity (speed and direction) will not change.
Question 17.
An airplane is moving uniformly at a constant height under the action of two forces (i) Upward force (lift) and (ii) Downward force (weight). What is the net force on the aeroplane?
Ans:
The aeroplane is moving uniformly (constant velocity) at a constant height.
According to Newton’s First Law of Motion, a body continues in its state of rest or uniform motion unless acted upon by a net external force. Since the velocity (speed and direction) of the aeroplane is constant (uniform motion), its acceleration is zero.
The condition for zero acceleration is that the net force acting on the body must be zero.
Since the aeroplane is moving at a constant height, it is in vertical equilibrium. This means the upward force (lift) and the downward force (weight) must be equal in magnitude.
Lift – Weight = 0
Therefore, the net force on the aeroplane is zero.
Question 18.
Why does a person fall when he jumps out from a moving train ?
Ans:
This phenomenon is best explained by Newton’s First Law of Motion, often called the Law of Inertia.
Here is the explanation:
Why a Person Falls
When a person is inside a moving train, their entire body (including internal organs and clothes) is moving forward at the same high velocity as the train.
- Initial State (Inertia of Motion): When the person jumps out, their body retains the inertia of motion and continues to move forward at the train’s high speed.
- Contact with Ground (Sudden Change): The moment the person’s feet touch the stationary ground, the friction between their shoes and the ground exerts a large, sudden backward force on their feet. This force rapidly brings the feet to rest.
- Upper Body Continues: Since there is no such immediate stopping force on the upper body, the upper body continues to move forward due to inertia.
- Result: The feet stop abruptly, but the upper body continues forward, causing the person to lose balance and fall forward in the direction the train was moving.
Question 19.
Why does a coin, placed on a card, drop into the tumbler when the card is rapidly flicked with a finger?
Ans:
The coin drops into the tumbler because of inertia of rest.
- Inertia of Rest: The coin is initially at rest and, due to its inertia, it tends to remain at rest.
- Force on the Card: When the card is rapidly flicked, a large external force acts only on the card, causing it to accelerate quickly and move out from under the coin.
- No Force on the Coin: Since the flicking force was not applied to the coin, and the flick was rapid (minimizing friction), the coin does not acquire enough horizontal velocity to move with the card.
- Gravity Takes Over: With the support (the card) suddenly removed, gravity becomes the dominant force acting on the coin, causing it to fall straight down into the tumbler.
Question 20.
Why does a ball thrown vertically upwards in a moving train , come back to the thrower’s hand ?
Ans:
The ball returns to the thrower’s hand because of inertia, specifically the shared horizontal velocity between the ball, the thrower, and the train.
Here is a short, unique explanation:
The moment the ball leaves the thrower’s hand, it possesses two key components of velocity:
- Vertical Velocity: Given by the thrower (upwards).
- Horizontal Velocity: Inherited from the moving train.
While the ball is in the air, the only force acting on it horizontally is air resistance (which is negligible for a short throw). Therefore, due to Newton’s First Law (Inertia), the ball continues to move forward horizontally at the same speed as the train and the thrower.
The thrower, the ball, and the train all travel the same horizontal distance during the time the ball is in the air, ensuring the ball lands precisely back in the thrower’s hand.
Question 21.
(a) Explain the following : When a train suddenly moves forward , the passenger standing in the compartment tends to fall backwards .
(b) Explain the following : When a corridor train suddenly starts , the sliding doors of some compartments may open.
(c) Explain the following:People often shake the branches of a tree to get its fruits down.
(d) Explain the following :After alighting from a moving bus , one has to run for some distance in the direction of the bus in order to avoid falling .
(e) Dust particles are removed from a carpet by beating it.
(f) Explain the following : It is advantageous to run before taking a long jump .
Ans:
These phenomena are all explained by the concept of Inertia, which is a body’s resistance to a change in its state of rest or motion.
(a) Passenger Tends to Fall Backwards
When a train suddenly moves forward, the lower part of the passenger’s body (feet) moves forward immediately with the train. However, the upper part of the body tends to remain in its state of rest due to inertia of rest. This lag causes the upper body to momentarily stay behind, making the passenger fall backward relative to the moving train.
(b) Sliding Doors Open When a Train Starts
When a stationary corridor train suddenly starts, the sliding doors, which are relatively loose, tend to remain in their state of rest due to inertia of rest. The body of the compartment moves forward, but the doors momentarily stay put. If the force of the push by the door frame on the door is not strong enough to overcome the door’s inertia, the door slides open backward relative to the train.
(c) Shaking Branches to Get Fruits Down
The fruits and the branches are initially at rest. When the branch is suddenly shaken, the branch moves, but the fruits tend to remain in their state of rest due to inertia of rest. The sudden movement breaks the weak connection (stem) between the fruit and the branch, causing the fruit to fall due to gravity.
(d) Running After Alighting from a Moving Bus
Before alighting, the passenger’s entire body is moving forward with the bus, possessing inertia of motion. When the feet touch the ground, they stop or slow down suddenly. However, the upper body tends to continue moving forward at the bus’s speed due to inertia of motion. To prevent the upper body from being thrown forward and causing a fall, one must run forward for a short distance to gradually reduce the forward momentum of the entire body.
(e) Dust Particles are Removed from a Carpet
When a carpet is beaten with a stick, the carpet is suddenly set into motion. The dust particles resting on the carpet, however, tend to remain in their state of rest due to inertia of rest. This sudden separation (carpet moves, dust stays) causes the dust to be dislodged and fall off due to gravity.
(f) Running Before Taking a Long Jump
It is advantageous to run before a long jump to build up inertia of motion (momentum). The forward momentum gained from running helps the jumper cover a greater horizontal distance during the jump. This built-up force of inertia allows the jumper’s body to carry on in the air for a longer duration and distance than if they jumped from a stationary position.
Exercise 3 (B)
Question 1.
The property of inertia is more in :
- a car
- a truck
- a horse cart
- a toy car
Question 2.
A tennis ball and a cricket ball , both are stationary. To start motion in them .
- less force is required for the cricket ball than for the tennis ball .
- a less force is required for the tennis ball than for the cricket ball
- The same force is required for both the balls .
- nothing can be said .
Question 3.
A force is needed to :
- Change the state of motion or state of rest of the body .
- Keep the body in motion
- keep the body stationary
- keep the velocity of the body constant .
Exercise 3 (C)
Question 1.
Name the two factors on which the force needed to stop a moving body in a given time depends.
Ans:
The two factors on which the force needed to stop a moving body in a given time depends are:
- Mass (m) of the body.
- Velocity (v) of the body (specifically, the change in velocity required,Δv).
This dependence is derived from the concepts of momentum and the impulse-momentum theorem:
- Momentum (p): Momentum is the product of mass and velocity (p = mv). The greater the initial momentum of the body, the greater the force required to stop it in a fixed time.
- Impulse-Momentum Theorem: Force (F) multiplied by the time interval (Δt) equals the change in momentum (Δp):F Since the time (Δt) is fixed, the required force is directly proportional to the change in momentum:
To stop a body, the change in momentum (Δp) is essentially equal to its initial momentum (mΔv). Therefore, F depends on both the mass (m) and the change in velocity (Δv).
Question 2.
Define linear momentum and state its S.I. unit.
Ans:
Here is the definition and unit for linear momentum.
Linear Momentum is defined as the product of the mass and the velocity of a moving object. It is a vector quantity, meaning it has both magnitude and direction. The direction of the linear momentum is the same as the direction of the object’s velocity.
S.I. Unit: kilogram metre per second (kg m/s).
Question 3.
A body of mass m moving with a velocity v is acted upon by a force. Write an expression for change in momentum in each of the following cases: (i) When v << c, (ii) When v → c and (iii) When v << c but m does not remain constant. Here, c is the speed of light.
Ans:
The change in momentum (Δp) is calculated as the final momentum (p₂) minus the initial momentum (p₁). The expression for momentum itself depends on the physical context, particularly the object’s velocity and mass.
Here are the expressions for the change in momentum in each case:
(i) When v << c (Classical/Newtonian Mechanics)
At speeds very small compared to light, mass is considered constant (invariant). Momentum is defined as p = mv.
- Expression for Change in Momentum:
Δp = p₂ – p₁ = mv₂ – mv₁ = m(v₂ – v₁)
This can also be written as Δp = mΔv, where Δv is the change in velocity.
(ii) When v → c (Relativistic Mechanics)
As velocity approaches the speed of light, relativistic effects dominate. Mass is no longer constant and increases with velocity. The relativistic momentum is p = γm₀v, where:
- m₀ is the rest mass.
- γ (gamma) is the Lorentz factor, given by γ = 1 / √(1 – v²/c²).
- Expression for Change in Momentum:
Δp = p₂ – p₁ = γ₂m₀v₂ – γ₁m₀v₁ = m₀(γ₂v₂ – γ₁v₁)
This expression accounts for the changes in both velocity and the relativistic gamma factor.
(iii) When v << c but m does not remain constant (Variable Mass System)
This case applies to systems like rockets or conveyors where the object’s mass changes, even at low speeds. The classical form p = mv still applies, but now mass (m) is a function of time, m(t).
- Expression for Change in Momentum:
The momentum is p(t) = m(t)v(t). The change in momentum is found using the product rule of calculus.
Δp = p₂ – p₁ = m₂v₂ – m₁v₁
For an infinitesimal change, the rate of change of momentum is dp/dt = (d(mv))/dt = v(dm/dt) + m(dv/dt).
Question 4.
Show that the rate of change of momentum = mass × acceleration. Under what condition does this relation hold?
Ans:
The derivation of Rate of change of momentum = mass × acceleration comes directly from applying the definition of momentum and the condition of constant mass.


Question 5.
Two bodies A and B of same mass are moving with velocities v and 2v, respectively. Compare their (i) inertia and (ii) momentum.
Ans:

Question 6.
Two balls A and B of masses m and 2 m are in motion with velocities 2v and v, respectively. Compare:
(i) Their inertia.
(ii) Their momentum.
(iii) The force needed to stop them at the same time.
Ans:
(i) Comparison of Inertia
Inertia is the measure of an object’s reluctance to have its state of motion altered. This property is determined exclusively by the object’s mass.
- Ball A possesses a mass of m.
- Ball B possesses a mass of 2m.
Since inertia is directly proportional to mass, Ball B, with twice the mass, has twice the inertia of Ball A. Therefore, the ratio of inertia of Ball B to Ball A is 2 : 1.

Question 7.
State Newton’s second law of motion. What information do you get from it?
Ans:


Question 8.
How does Newton’s second law of motion differ from the first law of motion?
Ans:
| Feature | Newton’s First Law (Law of Inertia) | Newton’s Second Law |
| Focus | Defines the conditions under which no change in motion occurs. | Defines the resulting change in motion (acceleration) when a net force is present. |
| Net Force (Fnet) | States that if Fnet=0, then acceleration (a) is zero, meaning velocity (v) is constant. | States that if Fnet=0, it produces acceleration (a). |
| Nature of Force | A qualitative statement. It conceptually defines what an external force is (something that changes an object’s state of motion). | A quantitative statement. It provides a way to measure the force required to cause a specific acceleration. |
| Mathematical Relation | Fnet=0⟹a=0 | Fnet=ma |
Question 9.
Write the mathematical form of Newton’s second law of motion. State the conditions if any. 10. State Newton’s second law of motion. Under what condition does it take the form F = ma?
Ans:
Newton’s Second Law of Motion: The Principle of Force and Change
Core Idea:
This law establishes a precise, measurable link between the force acting on an object and the change in its motion. It tells us that a force doesn’t just cause motion; it causes a change in motion.
Fundamental Statement:
The acceleration of an object is directly tied to the net force acting upon it and inversely tied to its mass. The resulting acceleration happens in the same direction as the net force.
The Relationship in Simple Terms:
- More Force, More Acceleration: If you push an object harder (increase the net force), its acceleration increases proportionally (assuming mass is constant).
- More Mass, Less Acceleration: If an object is heavier (has more mass), the same force will produce a smaller acceleration.
Mathematical Expression (The Common Form):
This relationship is most famously captured by the equation:
F_net = m a
Where:
- F_net is the net or unbalanced force acting on the object.
- m is the object’s mass.
- a is the acceleration that is produced.
The Deeper, More General Statement:
While F = m a is incredibly useful, it is actually a special case of a more fundamental law. The most complete statement of Newton’s Second Law deals with momentum.
Momentum (p) is defined as the product of mass and velocity (p = m v).
The law states: The net force acting on an object is equal to the rate at which its momentum changes over time.
This is written as: F_net = Δp / Δt
Where:
- Δp is the change in momentum.
- Δt is the change in time.
Connecting the Two Forms:
The equation F_net = m a is derived directly from the momentum form when the object’s mass remains constant.
Here is the step-by-step connection:
- Start with the general form: F_net = Δp / Δt
- Since momentum p = m v, a change in momentum is Δp = Δ(m v).
- If mass (m) is constant, it can be factored out: Δp = m Δv.
- Substitute back in: F_net = (m Δv) / Δt
- We know that the change in velocity over time (Δv / Δt) is the definition of acceleration (a).
- Therefore, the equation simplifies to the familiar form: F_net = m a
In Essence:
The form F_net = Δp / Δt is the universal and fundamental law. The form F_net = m a is its powerful and widely used simplification, which is valid for the vast majority of situations where an object’s mass does not change as it moves.
Question 11.
How can Newton’s first law of motion be obtained from the second law of motion?
Ans:
Newton’s second law provides the mathematical rule for how a force alters an object’s motion, stating that the net force on an object is directly proportional to the product of its mass and the acceleration it experiences (F_net = m × a).
The first law of motion can be logically deduced as a specific, foundational instance of this general rule. It describes the behavior of an object under a particular condition: when the total external force acting upon it is precisely zero.
By inserting this condition of zero net force (F_net = 0) into the equation of the second law, we get:
0 = m × a
Given that an object’s mass (m) is a positive, non-zero quantity, the only mathematical solution for this equation to hold true is for the acceleration (a) to also be zero. An acceleration of zero signifies no change in the object’s velocity. Consequently, the object must continue in its current state of motion indefinitely—whether that state is a constant velocity (which includes moving in a straight line at a steady speed) or a state of complete rest.
Thus, the first law is not an independent principle but rather the cornerstone consequence of the second law for the specific scenario where the net force is absent. It defines the natural state of motion for any object in the absence of external influences.
Question 12.
(a) Draw a graph to show the dependence of acceleration on force for a constant mass.
(b)Draw a graph to show the dependence of force on mass for a constant acceleration.
Ans:
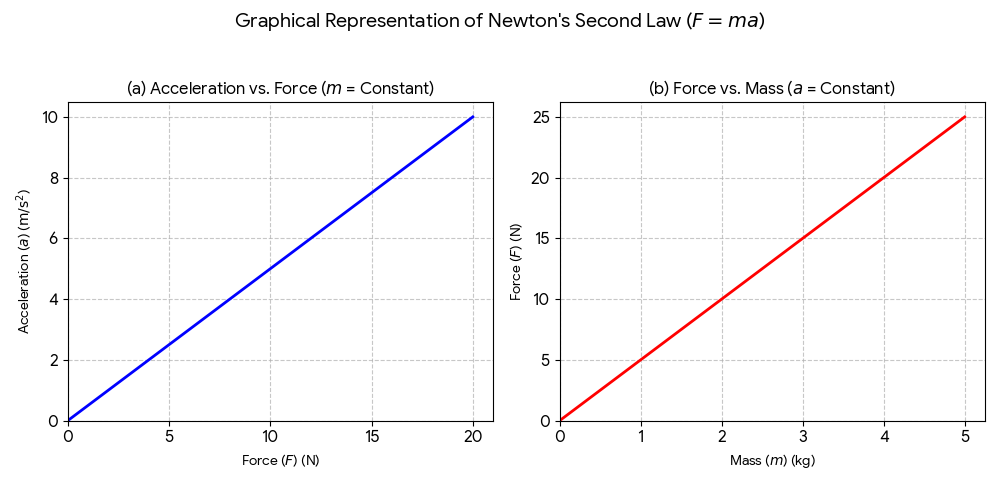


Question 13.
How does the acceleration produced by a given force depend on the mass of the body? Draw a graph to show it.
Ans:
The Relationship Between Force, Mass, and Acceleration
The acceleration produced by a given force is inversely proportional to the mass of the body.
This means that for a constant force:
- If the mass increases, the acceleration decreases.
- If the mass decreases, the acceleration increases.
This fundamental principle is at the heart of Newton’s Second Law of Motion, which is mathematically stated as Force = Mass × Acceleration (F = m × a).
Explanation
If we rearrange the formula to solve for acceleration, we get:
a = F / m
Since the force (F) is constant, the acceleration (a) depends only on the mass (m). The equation a = F / m clearly shows that acceleration is inversely proportional to mass. For example:
- If you push a lightweight toy car and a heavy real car with the same force, the toy car will gain much more speed (higher acceleration) than the heavy car.
- A rocket’s acceleration increases as it travels and its mass decreases by burning fuel, even if the thrust (force) remains constant.
Graph of Acceleration vs. Mass (for a Constant Force)
The graph showing the relationship between acceleration and mass is a downward-sloping curve, specifically a hyperbola.
Graph Description:
The Y-axis represents Acceleration (a).
The X-axis represents Mass (m).
The curve starts high on the left (where mass is small and acceleration is high) and slopes downward to the right, getting closer and closer to the x-axis but never actually touching it.
This shape visually confirms that as mass increases, acceleration approaches zero.
Acceleration (a)
↑
| *
| *
| *
| *
| *
| *
+——————> Mass (m)
(This is a text representation of a hyperbola. In a properly drawn graph, the curve would be a smooth hyperbola.)
Key Takeaway: The graph is a visual proof of the inverse relationship. Doubling the mass halves the acceleration, tripling the mass reduces acceleration to one-third, and so on.
Question 14.
Name the S.I. unit of force and define it .
Ans:

Question 15.
What is the C.G.S. unit of force? How is it defined?
Ans:
While we commonly use the newton to quantify a push or a pull, the dyne serves as its precursor in the centimetre-gram-second (C.G.S.) system. The dyne is fundamentally defined as the intensity of force needed to impart a specific change in motion to a specific mass. To be precise, a solitary dyne of force is at work when a mass of one gram experiences an increase in its velocity of one centimetre per second with each passing second. In essence, if you were to observe a one-gram object, such as a small paper clip, and see its speed steadily rising by a single centimetre per second for every second it is pushed, the force acting upon it would be exactly one dyne. This establishes its formal equivalence to one gram-centimetre per second squared (1 g·cm/s²), making it a much smaller unit of force compared to the newton, with one newton equaling 100,000 dynes.
Question 16.
Name the S.I. and C.G.S. units of force. How are they related?
Ans:
The standardized unit for measuring force in the International System (S.I.) is the Newton, represented by the symbol N.
In the Centimeter-Gram-Second (C.G.S.) system, the corresponding unit is the Dyne, with the symbol dyn.
Connecting the Two Units
The bridge between these units is built on the definition of force itself, derived from Newton’s principle: Force is the product of mass and the acceleration it produces.
By definition:
- A 1 Newton force is the push or pull that will change the speed of a 1-kilogram object by 1 meter per second, every second.
- A 1 Dyne force is the push or pull that will change the speed of a 1-gram object by 1 centimeter per second, every second.
To find their relationship, we translate the definition of 1 Newton into the units used for the Dyne:
1 N = (1 kg) × (1 m/s²)
Now, we convert the components:
- 1 kilogram is equivalent to 1000 grams.
- 1 meter is equivalent to 100 centimeters.
Substituting these values in:
1 N = (1000 g) × (100 cm/s²)
= 100,000 g·cm/s²
Since 1 g·cm/s² is, by definition, 1 Dyne, we conclude:
1 Newton = 100,000 Dynes, which can also be written scientifically as 1 N = 10⁵ dyn.
Question 17.
Why does a glass vessel break when it falls on a hard floor, but it does not break when it falls on a carpet?
Ans:
The difference lies in how the carpet and the hard floor manage the vessel’s momentum and the duration of the impact.
When the vessel falls, it gains a certain amount of momentum (mass x velocity) by the time it hits the ground. To bring the vessel to a stop, this momentum must be reduced to zero. The key factor is the rate at which this happens, which determines the force of the impact.
- On a Hard Floor: The surface is rigid and unyielding. The vessel comes to an abrupt, almost instantaneous stop. Because the stopping time is extremely short, the deceleration is very high. A large deceleration requires a massive force (as defined by Newton’s Second Law: Force = mass x acceleration). This immense, concentrated force far exceeds the structural strength of the glass, causing it to shatter.
- On a Carpet: The carpet fibres are compressible and act like a crude cushion. Upon impact, the carpet (and its padding) compresses over a few milliseconds. This significantly increases the duration of the impact. With more time to slow down, the vessel’s deceleration is much gentler. Since the deceleration is lower, the stopping force exerted on the glass is dramatically reduced. This weaker force remains below the breaking point of the glass, allowing the vessel to survive the fall.
In essence, the carpet doesn’t change the vessel’s momentum, but it spreads the stopping force over a longer time, making it less destructive.
Question 18.
(a) Use Newton’s second law of motion to explain the following instance :
A cricketer pulls his hands back while catching a fast moving cricket ball .
(b)Use Newton’s second law of motion to explain the following instance :
An athlete prefers to land on sand instead of hard floor while taking a high jump .
Ans:
(a) A cricketer pulls his hands back while catching a fast-moving cricket ball.
Explanation using Newton’s Second Law:
Newton’s second law of motion states that the force acting on an object is equal to the rate of change of its momentum, or F = ma (where F is force, m is mass, and a is acceleration).
- The fast-moving ball has a high momentum. To catch it, the cricketer must bring its momentum to zero.
- The force experienced by the cricketer’s hands is given by F = (Change in Momentum) / Time.
- If the ball is stopped abruptly (in a very short time, t), the rate of change of momentum is very high, resulting in a large force (F). This large force would hurt the hands.
- By pulling his hands back, the cricketer increases the time duration (t) over which the ball’s momentum comes to zero.
- According to the formula, for the same change in momentum, if the time t increases, the net force F decreases.
- Therefore, by increasing the stopping time, the cricketer reduces the force exerted on his hands, preventing injury and making it easier to secure the catch.
(b) An athlete prefers to land on sand instead of a hard floor while taking a high jump.
Explanation using Newton’s Second Law:
Newton’s second law (F = ma) is again the key principle here.
- When the athlete lands after a jump, their body’s vertical velocity must be brought to zero. This means their momentum must change to zero.
- The force experienced during landing is F = (Change in Momentum) / Time.
- A hard floor is rigid and unyielding. It brings the athlete to a stop in a very short time. This results in a very high rate of change of momentum, and consequently, a large upward force (F) acts on the athlete’s body. This large force can cause injuries like fractures or severe joint pain.
- Sand, on the other hand, is soft and compressible. When the athlete lands on sand, their feet sink into it.
- This action significantly increases the time duration (t) over which the athlete’s momentum is reduced to zero.
- Since the change in momentum is the same, a longer stopping time results in a much smaller force (F) being exerted on the athlete’s body.
- This reduced force minimizes the risk of injury, making the landing safer.
Exercise 3 (C)
1. The linear momentum of a body of mass m moving with velocity v is :
- v/m
- m/v
- mv
- 1/mv
Question 2.
The unit of linear momentum is :
- N s
- kg m s-2
- N s-1
- kg2 m s-1
Question 3.
The correct form of Newton’s second law is :
- F = Δp / Δt
- F =m Δv / Δt
- F = v Δm / Δt
- F = mv
Question 4.
The acceleration produced in a body by a force of given magnitude depends on
- size of the body
- shape of the body
- mass of the body
- none of these
Exercise 3 (C)
Question 1.
A body of mass 5 kg is moving with velocity 2 m s-1. Calculate its linear momentum.
Ans:
A body of mass 5 kg is moving with a velocity of 2 m s⁻¹. The formula used to calculate linear momentum (p) is the product of its mass (m) and its velocity (v).
p=m×v
p=m×v
Substituting the provided values into the formula:
P = (5 kg) ×(2 m s−1)
p=10 kg m s−1
Therefore, the linear momentum of the body is 10 kg m s⁻¹.
Question 2.
The linear momentum of a ball of mass 50 g is 0.5 kg m s-1. Find its velocity.
Ans:

Question 3.
A force of 15 N acts on a body of mass 2 kg. Calculate the acceleration produced.
Ans:
Step 1: Understand the Governing Principle
The fundamental rule of motion we apply here states that the acceleration an object experiences is a direct result of the force applied to it and is inversely related to its mass.
Step 2: List the Known Quantities
From the information provided:
- Applied Force (F) = 15 N
- Mass of the object (m) = 2 kg
Step 3: Apply the Conceptual Rule
The core relationship is that Acceleration is equal to Force divided by Mass. We express this mathematically to find our unknown.
Step 4: Perform the Calculation
Using the values:
Acceleration (a) = Force / Mass = 15 N / 2 kg
This gives the result:
a = 7.5 m/s²
Final Result:
The object will therefore accelerate at a rate of 7.5 meters per second squared.
Question 4.
A force of 10 N acts on a body of mass 5 kg. Find the acceleration produced.
Ans:
Step 1: Recall Newton’s Second Law
F = m × a
Step 2: Identify the Given Values
From the problem:
Force, F = 10 N
Mass, m = 5 kg
Step 3: Rearrange the Formula
We need to find acceleration (a). Rearranging the formula gives:
a = F / m
Step 4: Substitute the Values and Calculate
Substituting the known values into the equation:
a = 10 N / 5 kg
a = 2 N/kg
Since 1 Newton (N) is equivalent to 1 kg·m/s², the unit N/kg is the same as m/s².
a = 2 m/s²
Final Answer: The acceleration produced is 2 m/s².
Question 5.
Calculate the magnitude of force which when applied on a body of mass 0.5 kg produces an acceleration of 5 m s-2.
Ans:
To figure out how much push is required to get the object moving as described, we use the most basic law of motion. This rule simply says that the force you need is found by multiplying the object’s mass by how quickly you want it to speed up.
We can write this idea as a straightforward equation:
Force = Mass × Acceleration
From the details provided:
- The Mass of the object is 0.5 kilograms.
- The Acceleration we want it to achieve is 5 meters per second squared.
Putting these numbers into the equation looks like this:
Force = 0.5 kg × 5 m/s²
Doing the math:
0.5 times 5 equals 2.5.
When we combine the units of kilograms and meters-per-second-squared, we get the unit for force, which is the Newton.
So, the final answer is that a force of 2.5 Newtons is needed.
Question 6.
(a) A force of 10 N acts on a body of mass 2 kg for 3 s, initially at rest. Calculate : The velocity acquired by the body
(b) A force of 10 N acts on a body of mass 2 kg for 3 s, initially at rest. Calculate : Change in momentum of the body.
Ans:


Question 7.
(a) A force acts for 10 s on a stationary body of mass 100 kg, after which the force ceases to act. The body moves through a distance of 100 m in the next 5 s. Calculate: The velocity acquired by the body.
(b) A force acts for 10 s on a stationary body of mass 100 kg, after which the force ceases to act. The body moves through a distance of 100 m in the next 5 s. Calculate : The acceleration produced by the force
(c) A force acts for 10 s on a stationary body of mass 100 kg, after which the force ceases to act. The body moves through a distance of 100 m in the next 5 s. Calculate : The magnitude of the force
Ans:



Question 8.
Figure shows the velocity-time graph of a particle of mass 100 g moving in a straight line. Calculate the force acting on the particle.
(Hint : Acceleration = Slope of the v-t graph)
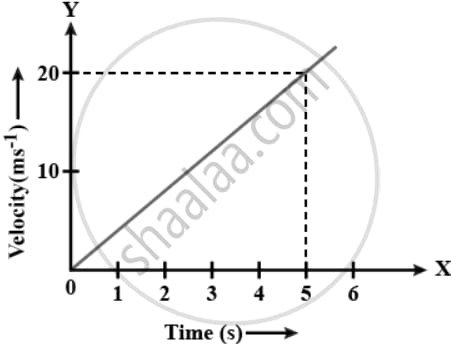
Ans:


Question 9.
A force causes an acceleration of 10 m s-2 in a body of mass 500 g. What acceleration will be caused by the same force in a body of mass 5 kg?
Ans:
Step 1: Determining the Force Applied
We start with the first object. It has a mass of 500 grams. To use standard physics formulas, we convert this into kilograms:
500 grams = 0.5 kilograms
This object accelerates at 10 m/s². According to Newton’s second law of motion, the force causing this acceleration is calculated by multiplying mass and acceleration:
Force (F) = mass × acceleration
F = 0.5 kg × 10 m/s²
F = 5 Newtons
So, the force being applied is 5 N.
Step 2: Calculating the New Acceleration
Now, we take the exact same 5 N force and apply it to the second object, which has a mass of 5 kg.
Using the same law, but now rearranged to solve for acceleration:
Acceleration (a) = Force / mass
Plugging in our values:
a = 5 N / 5 kg
a = 1 m/s²
Final Result
Therefore, when the same 5 Newton force acts on the 5 kg mass, it will produce an acceleration of 1 meter per second squared.
Question 10.
A force acts for 0.1 s on a body of mass 2.0 kg initially at rest. The force is then withdrawn and the body moves with a velocity of 2 m s-1. Find the magnitude of the force.
Ans:


Question 11.
A body of mass 500 g, initially at rest, is acted upon by a force which causes it to move a distance of 4 m in 2 s. Calculate the force applied.
Ans:
Step 1: Understanding the Problem
We are given:
- Mass of the body, m=500g=0.5kg
- Initial velocity, u=0m/s (since it starts from rest)
- Distance travelled, s=4m
- Time taken, t=2s We need to find the applied force, F.
- From Newton’s second law, F=ma.
We know the mass m, but we need to find the acceleration a.

Question 12.
A car of mass 480 kg moving at a speed of 54 km h-1 is stopped by applying brakes in 10 s . Calculate the force applied by the brakes .
Ans:


Question 13.
(a) A car is moving with a uniform velocity 30 ms-1. It is stopped in 2 s by applying a force of 1500 N through its brakes. Calculate the following values : The change in momentum of the car.
(b) A car is moving with a uniform velocity 30 ms-1. It is stopped in 2 s by applying a force of 1500 N through its brakes. Calculate the following values : The retardation produced in the car.
(c) A car is moving with a uniform velocity of 30 ms-1. It is stopped in 2 s by applying a force of 1500 N through its brakes. Calculate: The mass of the car.
Ans:


Question 14.
A bullet of mass 50 g moving with an initial velocity 100 m s-1 strikes a wooden block and comes to rest after penetrating a distance 2 cm in it. Calculate: (i) Initial momentum of the bullet, (ii) Final momentum of the bullet, (iii) Retardation caused by the wooden block and (iv) Resistive force exerted by the wooden block.
Ans:



Exercise 3 (D)
Question 1.
State the usefulness of Newton’s third law of motion .
Ans:
The usefulness of Newton’s Third Law of Motion lies in its fundamental explanation of how motion is generated and sustained through interaction between objects. It explains that forces never exist alone; they always occur in equal and opposite pairs.
The law’s primary usefulness is in:
- Explaining Propulsion and Movement: It is the underlying principle for all forms of locomotion.
- Walking/Running: You exert a backward action force on the ground due to friction; the ground exerts an equal and opposite forward reaction force that propels you forward.
- Rocket Propulsion: A rocket expels hot gas backward (action); the exhaust gas exerts an equal and opposite force, or thrust, on the rocket, pushing it forward (reaction).
- Engineering and Design: It is critical for calculating the forces on structures, vehicles, and machinery.
- Engineers use it to design bridges and buildings, ensuring the structure can withstand the equal and opposite reaction forces exerted by the ground, wind, or internal loads.
- It is fundamental in aerospace engineering for calculating lift and thrust in aircraft and spacecraft.
- Understanding Stability (Static Equilibrium): The law helps analyze why stationary objects remain at rest. For a book resting on a table, the book exerts a downward force (action) on the table, and the table exerts an equal and opposite upward force (normal force, reaction) on the book, resulting in a net force of zero on the book.
- Deriving the Law of Conservation of Momentum: The Third Law is essential for proving that in a closed system, the total momentum remains constant, which is a powerful tool for analyzing collisions and explosions.
Question 2.
State Newton’s third law of motion.
Ans:
Newton’s third law of motion, often called the Law of Action and Reaction, is formally stated as:
For every action, there is an equal and opposite reaction.
This means that whenever one object exerts a force on a second object (the action), the second object simultaneously exerts a force of equal magnitude and in the opposite direction on the first object (the reaction).
- These forces always occur in pairs.
- The forces act on two different objects, which is why they do not cancel each other out.
For example, when a rocket pushes hot gas downward (action), the gas pushes the rocket upward with the same amount of force (reaction/thrust).
Question 3.
State and explain the law of action and reaction. by giving two examples.
Ans:
The Law of Action and Reaction is Newton’s Third Law of Motion.
Statement of the Law
Newton’s Third Law of Motion states:
For every action, there is an equal and opposite reaction.
This means that forces always occur in pairs. If object A exerts a force on object B (the action), then object B simultaneously exerts a force of equal magnitude and opposite direction on object A (the reaction). These action and reaction forces never act on the same object.
Examples
1. Rocket Propulsion
- Action: The rocket engine rapidly burns fuel, creating hot gases that are forcefully expelled downward out of the exhaust nozzle.
- Reaction: The expelled gases exert an equal and opposite force upward on the rocket body. This reaction force is called thrust, and it is what propels the rocket into space. The rocket doesn’t need to push against the air or the ground; it pushes against the mass of its own exhaust gas.
2. A Person Walking
- Action: When a person walks, their foot pushes the ground backward and slightly downward (due to friction).
- Reaction: The ground simultaneously pushes the foot (and thus the person) with an equal and opposite force that is forward and slightly upward. This forward component of the reaction force is what accelerates the person and allows them to move.
Question 4.
(a) Name and state the action and reaction in the following case : Firing a bullet from a gun
(b) Name and state the action and reaction in the following case : Hammering a nail
(c) Name and state the action and reaction in the following case : A book lying on a table
(d) Name and state the action and reaction in the following case : A moving rocket
(e) Name and state the action and reaction in the following case : A person moving on the floor
(f) Name and state the action and reaction in the following case : A moving train colliding with a stationary train
Ans:
The Law of Action and Reaction
The Law of Action and Reaction is Newton’s Third Law of Motion, which states:
For every action, there is an equal and opposite reaction.
In an interaction between two objects, the forces they exert on each other are equal in magnitude and opposite in direction, and they act on different objects.
(a) Firing a bullet from a gun
| Interaction | Name of Force | Object it Acts On |
| Action | Force exerted by the gun on the bullet | Bullet |
| Reaction | Force exerted by the bullet on the gun | Gun |
| Result | The gun recoils (moves backward). |
(b) Hammering a nail
| Interaction | Name of Force | Object it Acts On |
| Action | Force exerted by the hammer on the nail | Nail |
| Reaction | Force exerted by the nail on the hammer | Hammer |
| Result | The nail is driven into the wood, and the hammer’s motion is stopped or reversed. |
(c) A book lying on a table
| Interaction | Name of Force | Object it Acts On |
| Action | Weight of the book (Gravitational force exerted by the Earth on the book) | Book |
| Reaction | Normal Force exerted by the table on the book (or the force exerted by the book on the Earth) | Book (or Earth) |
| Result | The book remains at rest because the Normal Force balances the weight. |
(d) A moving rocket
| Interaction | Name of Force | Object it Acts On |
| Action | Force exerted by the rocket on the exhaust gases (pushing the gases backward) | Exhaust Gases |
| Reaction | Force exerted by the exhaust gases on the rocket | Rocket |
| Result | This reaction force is called thrust, which propels the rocket forward. |
(e) A person moving on the floor
| Interaction | Name of Force | Object it Acts On |
| Action | Force exerted by the foot on the floor (pushing backward) | Floor |
| Reaction | Force exerted by the floor on the foot (pushing forward due to friction) | Person |
| Result | The forward reaction force accelerates the person. |
(f) A moving train colliding with a stationary train
| Interaction | Name of Force | Object it Acts On |
| Action | Force exerted by the moving train on the stationary train | Stationary Train |
| Reaction | Force exerted by the stationary train on the moving train | Moving Train |
| Result | Both trains exert forces of equal magnitude on each other, causing the momentum of the system to be conserved. The moving train slows down, and the stationary train moves forward. |
Question 5.
Explain the motion of a rocket with the help of Newton’s third law.
Ans:
The motion of a rocket is an excellent demonstration of Newton’s Third Law of Motion, which states that for every action, there is an equal and opposite reaction.
How Rocket Propulsion Works
The rocket system involves an interaction between the rocket body and the exhaust gases it expels.
- Action Force (The Push):
- Inside the rocket’s combustion chamber, fuel and oxidizer are burned, generating a massive volume of hot, high-pressure gases.
- The rocket engine forces these gases out of the exhaust nozzle at extremely high velocity in the downward (or backward) direction.
- The action is the large, forceful push exerted by the rocket on the exhaust gases.
- Reaction Force (Thrust):
- In accordance with Newton’s Third Law, the exhaust gases exert an equal and opposite force back on the rocket body.
- This resulting reaction force is called Thrust, and it acts in the upward (or forward) direction, propelling the rocket off the launch pad and into space.
Question 6.
When a shot is fired from a gun, the gun is recoiled. Explain.
Ans:
The backward jerk experienced when firing a gun, commonly known as “kickback,” is a direct result of a fundamental physical rule concerning motion.
To understand this, imagine the gun and the bullet inside it as a single, isolated pair. Before the trigger is pulled, this pair is completely still. Its overall tendency to move—its combined momentum—is precisely zero.
The process is set in motion by the ignition of the gunpowder. This creates a rapidly expanding gas that acts like a powerful spring, pushing in all directions within the confined barrel. It applies intense pressure, launching the bullet forward. However, the gas presses with identical strength against the back of the gun’s chamber.
This creates a pair of opposing pushes. While the bullet is driven forward down the barrel, the gun itself is driven backward with equal force. This isn’t merely a reaction in the everyday sense; it is a strict, one-to-one physical exchange.
Because momentum must be preserved and the system started with a total of zero, it must end with zero. The lightweight bullet races away with a certain amount of forward momentum. To perfectly counterbalance this, the much heavier gun must acquire an equal amount of momentum in the reverse direction. Since the gun’s mass is vastly greater, it achieves this balance by moving backward at a significantly slower speed. This backward motion is the recoil we feel—a powerful, sudden shove against the shooter’s hand and shoulder.
In essence, the gun is not just “reacting” to the bullet’s launch; it is an active participant in a forced exchange of motion, compelled by nature’s law to balance the scales.
Question 7.
When you step ashore from a stationary boat, it tends to leave the shore. Explain.
Ans:
This phenomenon is a perfect illustration of Newton’s Third Law of Motion (The Law of Action and Reaction) and the Conservation of Momentum.
Explanation using Newton’s Third Law
- Action: As you step forward toward the shore, your feet exert a forceful push backward on the boat. This is the action force.
- Reaction: According to Newton’s Third Law, the boat exerts an equal and opposite force forward on your body, propelling you onto the shore. This force is the reaction force.
- Result: Since the boat is resting on the water (a low-friction surface), the backward force from your push causes it to move away from the shore (recede) as you move forward.
Explanation using Conservation of Momentum
The principle of conservation of momentum also applies here:
- Before: Before you step, the total momentum of the boat-person system is zero, as both are stationary.

Question 8.
When two spring balances joined at their free ends are pulled apart, both show the same reading. Explain.
Ans:
When two spring balances joined at their free ends are pulled apart, both show the same reading because of Newton’s Third Law of Motion, the Law of Action and Reaction.
Explanation
- The Interaction: The two spring balances, let’s call them Balance A and Balance B, interact directly with each other at the point where they are joined.
- Action Force: When you pull on Balance A, it transmits a force to Balance B. This force is the action force exerted by Balance A on Balance B.
- Reaction Force: According to Newton’s Third Law, Balance B simultaneously exerts an equal and opposite force back on Balance A. This is the reaction force exerted by Balance B on Balance A.
- Reading the Balances:
- Balance B reads the magnitude of the force acting on its hook (the action force from A).
- Balance A reads the magnitude of the force acting on its hook (the reaction force from B).
Since the law dictates that the magnitude of the action force and the reaction force must be equal , both spring balances will always display the same numerical reading, regardless of how hard they are pulled, as long as they are connected and the system is in equilibrium or accelerating together.
This demonstrates that forces always exist as mutual, equal, and opposite pairs.
Question 9.
To move a boat ahead in water, the boatman has to push the water backwards by his oar. Explain this statement.
Ans:
The movement of a rowboat is a clever trick played with forces, where the real push comes from an unexpected source. The rower’s effort doesn’t pull the boat forward; it instead creates a situation where the water itself does the pushing.
It begins with the oar. When the blade is driven backward through the water by the rower’s pull, it acts like a solid wall shoving against the water. This action forces a mass of water to move backward.
The water resists this displacement. It pushes back against the face of the oar blade with a strength that matches the force the rower applied. This resistance from the water is not random; it is a direct and equal reply, aimed in the exact opposite direction—forward.
The oarlock is the crucial pivot in this exchange. It acts as a fulcrum, allowing the rower’s backward pull on the handle to be converted into a backward push by the blade. Because this pivot is attached to the boat, the forward-pushing answer from the water is transferred through the oar and into the hull.
So, the boat is not being dragged forward by the oar. It is being shoved from the front by the reactive push of the water, a force generated only because the rower first used the oar to push water the other way. The rower, in essence, uses the water as a solid anchor against which to lever the boat ahead.
Question 10.
A person pushing a wall hard is liable to fall back. Give a reason.
Ans:
A person pushing a wall hard is liable to fall back because of Newton’s Third Law of Motion, the Law of Action and Reaction.
Here is the explanation:
- Action Force: When the person pushes the wall, they exert a large force on the wall in the forward direction. This is the action force.
- Reaction Force: According to Newton’s Third Law, the wall simultaneously exerts an equal and opposite force back on the person. This reaction force is directed backward.
- Result: Since the reaction force from the wall acts on the person’s body and is directed backward, it can easily overcome the friction between the person’s feet and the floor (especially if the floor is slippery). This unbalanced backward force causes the person to accelerate backward, making them liable to fall back.
In short, the force that makes the person fall backward is the reaction force from the wall, which is equal in magnitude to the effort (action) the person puts into the push.
Question 11.
The action and reaction both act simultaneously. Is this statement true?
Ans:
Yes, the statement is true.
Newton’s Third Law of Motion states that forces always occur in equal and opposite pairs known as the action-reaction pair. A key characteristic of these pairs is that they are simultaneous.
There is no time delay between the action force and the reaction force. As soon as the “action” force is exerted by one object on a second object, the “reaction” force is exerted back on the first object.
For example, when you press your finger against a desk, the instant your finger exerts a downward force on the desk, the desk exerts an equal and opposite upward force back on your finger.
Question 12.
The ‘Action and reaction are equal in magnitude’. Is this statement true?
Ans:
Yes, the statement “Action and reaction are equal in magnitude” is absolutely true.
It is a core part of Newton’s Third Law of Motion, which states:
However, the full truth and its implications are often misunderstood. Here’s a more precise breakdown:
1. What “Equal and Opposite” Means
- Equal in Magnitude: The force with which Object A pushes (or pulls) Object B is exactly the same size as the force with which Object B pushes (or pulls) back on Object A.
- Opposite in Direction: These two forces always act in precisely opposite directions (180° apart).
2. The Crucial Clarification (Why it Can Be Confusing)
While the forces are equal and opposite, they do not cancel each other out. This is because they act on two different objects.
- The action force acts on Object B.
- The reaction force acts on Object A.
Since each force in the pair acts on a different object, they cannot balance each other for a single object. Each force affects the motion of the object it is applied to.
Examples to Illustrate:
1. Walking:
- Action: Your foot pushes backward on the ground.
- Reaction: The ground pushes forward on you with an equal force.
- Result: The force on you (from the ground) propels you forward. The force on the Earth is also immense, but because the Earth’s mass is so large, its acceleration is imperceptible.
2. A Book on a Table:
- Action: The book’s weight pulls it down onto the table (a force on the table).
- Reaction: The table pushes upward on the book with an equal force (the normal force).
- Result: The book remains at rest because the upward force on it balances its weight (this is now Newton’s First Law). The downward force on the table is balanced by the floor’s support.
3. Rocket Launch:
- Action: The rocket engine pushes hot gases downward.
- Reaction: The hot gases push the rocket upward with an equal force.
- Result: The rocket accelerates upward.
Conclusion:
The statement is true, but it’s essential to remember the complete picture: the equal and opposite forces always act on two different objects, which is why motion can still occur.
Question 13.
A light ball falling on ground, after striking the ground rises upwards. Explain the reason.
Ans:
A ball’s rebound is a vivid demonstration of energy changing forms and a forceful reply from a seemingly passive surface. The core of the bounce lies in the ball’s temporary transformation and the ground’s unyielding nature.
The process begins the moment the ball makes contact. The ball’s downward journey, driven by gravity, gives it kinetic energy—the energy of motion. Upon impact, this motion doesn’t simply vanish. Instead, it is converted into potential energy stored within the ball itself. The ball’s material is compressed, like a spring being pressed down. In this squashed state, the ball exerts a significant downward force on the ground.
Here, the ground’s role is active, not passive. Because the ground is rigid and fixed, it cannot move away. It resists the ball’s compression with an equal and opposite upward force. This isn’t a gentle nudge; it is a powerful, elastic shove.
This upward force from the ground does two critical things in rapid succession. First, it acts as a brake, arresting the ball’s downward plunge completely. Second, it becomes the engine for the ascent. The compressed ball now has a command to move upward, and its own material, straining to return to its natural shape, provides an extra boost. The stored potential energy is rapidly converted back into kinetic energy.
This combination—the ground’s propulsive upward force and the ball’s own elastic recovery—launches the ball back into the air. The downward energy is not destroyed; it is redirected upward, with the ball and the ground working in a brief, powerful partnership to reverse the direction of travel. The bounce is the ball’s stored energy reclaiming its form as motion.
Question 14. Comment on the statement ‘the sum of action and reaction on a body is zero’.
Ans:
The statement, ‘the sum of action and reaction on a body is zero,’ is a common but fundamentally incorrect interpretation of Newton’s Third Law. While it sounds plausible, it misapplies the principle in a way that contradicts the very reason objects move.
The critical error lies in the phrase “on a body.”
Newton’s Third Law states that forces always exist in pairs: if Object A exerts a force on Object B (the action), then Object B simultaneously exerts an equal and opposite force on Object A (the reaction). The crucial point is that these two forces never act on the same body.
- The action force acts on Object B.
- The reaction force acts on Object A.
Therefore, you cannot “sum” these forces together for a single body because they are applied to different objects. Each force in the pair has a single, separate target.
Consider a simple example: Your hand pushing a book.
- Action: Your hand exerts a forward force on the book.
- Reaction: The book exerts an equal backward force on your hand.
Now, let’s apply the faulty statement:
- What is the sum of forces on the book? It is just the forward force from your hand. The reaction force (the backward force on your hand) does not act on the book, so it cannot be added to the book’s forces to make zero. This is why the book accelerates forward.
- What is the sum of forces on your hand? It is the backward force from the book. The action force (the forward force on the book) does not act on your hand, so it cannot cancel anything out. You feel this backward force as a push against your palm.
The forces are equal and opposite, but they do not cancel each other because they are not applied to the same object. They are two separate events happening to two different bodies simultaneously.
In summary, the statement is false. The law describes a pair of forces acting on two different bodies, which is precisely why they can cause motion rather than prevent it. You can only correctly sum forces to zero when considering all forces acting on a single, specific object to determine if it is in equilibrium, a concept governed by Newton’s First Law, not the Third.
Exercise 3 (D)
Question 1.
Newton’s third law :
- defines the force qualitatively
- Defines the force quantitatively.
- Explains the way the force acts on a body .
- Gives the direction of force.
Question 2.
Action and reaction act on :
- Same body in opposite directions.
- Different bodies in opposite directions.
- Different bodies , but in the same direction.
- Same body in the same direction.
Exercise 3 (D)
Question 1.
A boy pushes a wall with a force of 10 N towards east. What force is exerted by the wall on the boy?
Ans:
The force exerted by the wall on the boy is 10 N towards west.
This is explained by Newton’s Third Law of Motion (the Law of Action and Reaction), which states that for every action force, there is an equal and opposite reaction force.
- Action Force (Boy on Wall): 10 N towards East.
- Reaction Force (Wall on Boy): Must have an equal magnitude (10 N) and opposite direction (West).
Question 2.
In the Figure a block of weight 15 N is hanging from a rigid support by a string. What force is exerted by (a) a block on the string and (b) a string on the block? Name and show them in the diagram.

Ans:
Based on the provided figure and the principles of Newton’s laws of motion, here is the explanation of the forces involved.
Forces Exerted
(a) Force Exerted by the Block on the String (Action Force)
The block exerts a force on the string due to its weight pulling downward.
- Force: 5N
- Direction: Vertically downward.
- Name: This is the Action Force (or the tension pull exerted by the block).
(b) Force Exerted by the String on the Block (Reaction Force)
According to Newton’s Third Law (Action-Reaction), the string exerts an equal and opposite force on the block. Since the block is stationary (in equilibrium), this upward force must also balance the block’s weight.
- Force: 15 N
- Direction: Vertically upward.
- Name: This is the Reaction Force (or the tension in the string) and is also called the Tension Force (T).
Forces Shown in the Diagram
The image below conceptually shows the two forces acting on the respective objects:
- The force exerted by the block on the string acts at the bottom end of the string, pointing down.
- The force exerted by the string on the block acts at the top surface of the block, pointing up.
Exercise 3 (E)
Question 1.
Write the answer of the question with reference to laws of gravitation.
State the universal law of gravitation.
Ans:
The Universal Law of Gravitation was formulated by Sir Isaac Newton.
Statement of the Universal Law of Gravitation
The law states that:
Every particle in the universe attracts every other particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers.
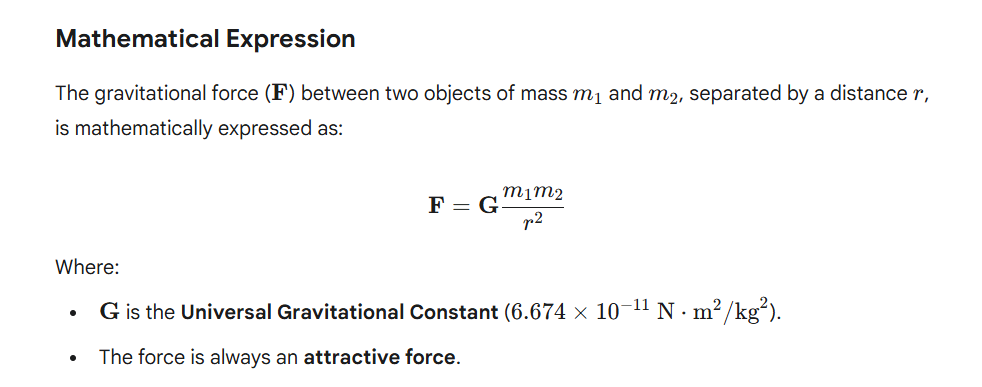
Question 2.
State whether the gravitational force between two masses is attractive or repulsive ?
Ans:
The gravitational force between any two masses is always attractive.
It is a fundamental property of gravitation that it only pulls masses towards each other; it never pushes them apart.
Question 3.
Write an expression for the gravitational force of attraction between two bodies of masses m1 and m2 separated by a distance r.
Ans:

Question 4.
How does the gravitational force of attraction between two masses depend on the distance between them?
Ans:
The gravitational pull between two objects weakens dramatically as they move apart. This relationship is not a simple, gradual decline but follows a specific and powerful mathematical principle.
Imagine the force of gravity as a kind of influence that spreads out in all directions from an object. As this influence travels outward, it doesn’t just thin out—it spreads over an ever-increasing area.
This is where the key insight lies: the strength of the force is tied to the square of the distance between the centers of the two objects. In practical terms, this means if you double the distance separating two masses, the gravitational force between them does not halve; it becomes four times weaker (because 2 multiplied by itself is 4).
If you were to triple the distance, the force becomes nine times weaker (3 x 3 = 9). Conversely, bringing them closer has the opposite, supercharged effect. Halving the distance makes the attraction four times stronger.
So, the dependence is one of intense sensitivity. A small increase in distance leads to a large drop in gravitational pull, governed by this “inverse-square” law, where the force is inversely proportional to the square of the distance that separates them.
Question 5.
How is the gravitational force between two masses affected if the separation between them is doubled?
Ans:
The strength of gravity doesn’t just fade as objects move apart; it collapses at a startling rate. This relationship is one of the most precise in all of physics.
Picture the gravitational attraction not as a simple thread that stretches, but as an influence that must cover an ever-expanding area.
When you double the distance between two objects, you aren’t simply making the gap twice as wide. You are increasing the spherical “zone” over which the gravitational influence must be shared by a factor of four. The force, in effect, becomes four times more diluted. Consequently, the p ull you feel at that new distance is only one-quarter as strong.
The effect is dramatic. Triple the original distance, and the force weakens to a mere one-ninth. Increase the gap tenfold, and the gravitational attraction becomes a feeble one-hundredth of what it once was.
This is why the planets remain steadfast in their orbits around the immensely massive Sun, yet you don’t feel any gravitational tug from the person standing next to you. Gravity is a powerful force, but it is also a fiercely local one, weakening so drastically with distance that its reach is both infinite and intimately limited.
Question 6.
Define gravitational constant G.
Ans:
Think of the gravitational constant, G, as the universe’s precise scaling factor for gravity. It is a fixed number that reveals the exact strength of the invisible pull between any two pieces of matter in the cosmos.
While Isaac Newton revealed that every object attracts every other object with a force proportional to their masses and inversely proportional to the square of the distance between them, his law was incomplete without a key piece of information: exactly how strong is this attraction? The constant G provides that critical answer.
It is the definitive numerical value that plugs into Newton’s equation to make it work perfectly. In the formula for universal gravitation:
F = G (m₁m₂)/r²
G is the fundamental proportionality constant. Its value is exceptionally small, which is why we don’t feel the gravitational pull of everyday objects. This tiny number means that gravity is, in fact, the weakest of the fundamental forces, but its reach is infinite.
Unlike “g” (the acceleration due to gravity on Earth, which is about 9.8 m/s² and changes from planet to planet), G is truly universal. It is a fundamental physical constant, meaning its value is the same everywhere in the universe—in our solar system, in a distant galaxy, and everywhere in between. It is the precise numerical key that allows us to calculate the gravitational force not just between apples and the Earth, but also between planets, stars, and galaxies.
Question 7.
Write the numerical value of gravitational constant G with its S.I. unit .
Ans:
The numerical value of the gravitational constant, denoted by G, is approximately:
6.67430 × 10⁻¹¹
Its S.I. unit is:
Newton metre squared per kilogram squared (N·m²/kg²)
This unit directly comes from Newton’s law of universal gravitation: F = G(m₁m₂)/r², where force is in Newtons (N), mass in kilograms (kg), and distance in metres (m).
Question 8.
What is the importance of the law of gravitation ?
Ans:
The true importance of the law of gravitation lies in its power to shatter the ancient belief that the heavens and the Earth operated under different sets of rules. Before this law, the force that made an apple fall was thought to be entirely separate from the force that guided the moon. This concept unified our world with the cosmos.
Its significance unfolds in several profound ways:
First, it gave us a key to the sky. This single, mathematical principle finally explained the graceful, elliptical orbits of the planets that had puzzled astronomers for centuries. It wasn’t a mysterious divine influence, but a predictable, calculable force of attraction between the Sun and the planets. This single law explained not only orbits but also the ocean’s tides, revealing them as a gentle, cosmic tug-of-war between the Earth, Moon, and Sun.
Second, it transformed us from passive observers into active predictors. By using this law, scientists could not only chart the path of known planets but also predict the existence of new ones. The discovery of Neptune was a monumental triumph—a planet found not by chance, but by calculating its gravitational pull on its neighbor, Uranus. This cemented the law’s power as a tool for discovery.
Furthermore, it provides the fundamental architecture of our universe. It is the great organizer, the force that gathers scattered gas into stars, binds stars into galaxies, and holds our feet firmly on the ground. It is the cosmic glue that shapes the large-scale structure of everything we see.
Finally, this centuries-old law is the very foundation of our modern space age. Every satellite circling our planet, every spacecraft we send to Mars, and every astronaut walking on the Moon relies on our precise understanding of this universal pull. We use its principles not as a chain that binds us to Earth, but as a roadmap to navigate away from it.
In essence, the law of gravitation did more than explain a force; it connected the mundane to the magnificent, giving us the confidence to believe that the universe is knowable, predictable, and within our reach to explore.
Question 9.
What do you understand by the term force due to gravity ?
Ans:
The force due to gravity is the natural, invisible pull that one mass exerts on another. It is an attraction that doesn’t require any direct contact to work, drawing objects toward each other.
We most commonly experience this force as the unwavering pull of the Earth itself. This specific pull is what we call an object’s weight. It is the reason why, when you let go of something, it doesn’t hover but falls straight toward the ground. This force is also what gives us our sense of heaviness.
This pull isn’t one-sided. While the Earth tugs on you, you are also, in fact, pulling the Earth toward you with a force of identical strength. However, because the Earth’s mass is incomprehensibly larger, its resistance to moving (its inertia) is equally vast. The result is that you move dramatically toward the Earth, while the Earth’s movement toward you is immeasurably small.
The strength of this gravitational pull isn’t fixed. It depends directly on mass and distance. The more massive an object, the stronger its gravitational tug. Conversely, as the distance between two objects grows, the gravitational force between them weakens rapidly—in fact, it weakens by the square of the distance.
In essence, the force due to gravity is the universe’s way of ensuring that all things with mass are in a constant, silent dance of mutual attraction, an attraction we feel most powerfully as the ground holding us firmly in place.
Question 10.
Write an expression for the force due to gravity on a body of mass m and explain the meaning of symbols used in it.
Ans:
The expression for the force due to gravity acting on a body of mass m when it is on or near the surface of the Earth is:
F = m g
Here is the meaning of each symbol in this expression:
- F: This represents the force due to gravity, which we commonly call the object’s weight. It is a vector quantity, meaning it has both magnitude (a value) and direction (which is always straight down, towards the center of the Earth). It is measured in Newtons (N).
- m: This is the mass of the body. Mass refers to the amount of matter the object contains and is a measure of its inertia. It is a scalar quantity, meaning it only has magnitude. It is measured in kilograms (kg).
- g: This symbol represents the acceleration due to gravity. On the surface of the Earth, its average value is approximately 9.8 m/s². This is not a constant for the universe; it is a value that depends on the mass and radius of the celestial body (like Earth). It tells us how quickly the speed of any freely falling object increases every second, due to Earth’s gravitational pull. Its units are meters per second squared (m/s²).
In essence, the formula F = m g tells us that an object’s weight is the direct result of planetary gravity accelerating its mass.
Question 11.
Define the term acceleration due to gravity? Write its S.I. unit.
Ans:
Acceleration due to gravity is the steady gain in speed that a object experiences when it is allowed to fall freely under the influence of a celestial body’s gravitational pull, without any other forces (like air resistance) acting upon it. It is the rate at which the velocity of a freely falling object increases every second.
For Earth, this value is approximately 9.8 meters per second every second. This means that if you were to drop an object in a vacuum, its downward speed would increase by 9.8 m/s with each passing second.
Its S.I. unit is the meter per second squared (m/s²).
Question 12.
Write down the average value of g on Earth’s surface ?
Ans:
The average value of the acceleration due to gravity (g) on the Earth’s surface is 9.8 meters per second squared (m/s²).
This is the standard figure used for calculations in textbooks and classroom settings. It’s important to know this is an average because the exact value changes slightly depending on where you are. It increases a tiny bit at the poles and decreases slightly at the equator due to the Earth’s rotation and its slightly flattened shape. Altitude also plays a role, with gravity weakening as you go higher.
So, while 9.8 m/s² is the universally accepted average, the actual force you feel pulling you down varies ever so slightly across the planet.
Question 13.
How is the acceleration due to gravity on the surface of the earth related to its mass and radius ?
Ans:
The acceleration due to gravity on Earth’s surface is a direct consequence of our planet’s mass and a powerful demonstration of how its size concentrates that pull. The relationship is defined by a specific physical law and can be understood in two parts:
1. The Pull of Mass:
At its heart, gravity is the force of attraction between masses. The Earth’s immense mass creates a gravitational field that pulls objects toward its center. If Earth were more massive, its gravitational tug would be stronger. Therefore, the acceleration due to gravity is directly proportional to the Earth’s mass. A planet with twice the mass would, all else being equal, have twice the surface gravity.
2. The Concentration of that Pull:
However, the strength of this pull at the surface doesn’t just depend on the total mass, but on how close you are to the center of that mass. We experience gravity on the surface, and the Earth is a sphere. This is where the radius becomes critical.
The gravitational pull weakens with the square of the distance from the planet’s center. This is known as an inverse-square law. The planet’s radius is precisely that starting distance. If you were to magically double the Earth’s radius without changing its mass, you would be standing twice as far from the center. The gravitational force would then be spread over a much larger area and would be only one-quarter of its original strength. Therefore, the acceleration due to gravity is inversely proportional to the square of the Earth’s radius.
The Combined Relationship:
These two factors combine into a single precise relationship. The acceleration due to gravity (*g*) is equal to the Universal Gravitational Constant (G) multiplied by the Earth’s mass (M), and then divided by the square of the Earth’s radius (R).
In simple terms: g = G M / R²
This formula shows that a large mass increases *g*, while a large radius decreases it. Our experience of gravity’s strength is the result of our planet’s total mass being packaged within a specific, finite size.
Question 14.
How are g and G related ?
Ans:
Think of G and g as a universal rule and its local outcome. They are fundamentally connected, but they describe gravity at two completely different scales.
G, the Universal Gravitational Constant, is a fixed number. It’s a fundamental law of nature that tells us how strong the gravitational pull is between any two bits of mass in the entire universe. It never changes.
g, on the other hand, is the local result of that law in a specific situation. It’s the rate at which an object speeds up as it falls near a celestial body like Earth. Its value changes depending on where you are.
Here is the precise connection:
The value of g on a planet’s surface is a direct consequence of the universal law G. It is calculated using the mass of the planet (M) and its radius (R), following this specific relationship:
g = (G * M) / R²
Let’s break this down:
- G is the universal constant, the fixed rule of attraction.
- M is the mass of the planet (e.g., Earth).
- R is the distance from the planet’s center (its radius, if you’re on the surface).
The formula shows that the acceleration we experience as gravity (g) is produced by the planet’s mass (M), with the strength dictated by the universal constant (G), and weakened by the square of our distance from the planet’s center.
In essence, G is the cause—the fundamental law of gravity. g is the effect—the specific acceleration we experience because of that law acting on us through Earth’s mass.
Question 15.
A body falls freely under gravity from rest and reaches the ground in time t. Write the expression for the height fallen by the body.
Ans:
Imagine dropping a stone from a great height. It doesn’t simply fall at a steady pace; it gathers speed, hurtling downward faster with every passing moment. This ever-increasing velocity is the work of gravity’s constant tug, and it creates a fascinating relationship between the time spent falling and the distance covered.
The connection is not linear, where doubling the time would simply double the distance. Instead, it is a square relationship. The distance the stone plummets is proportional to the square of the time it has been falling.
We capture this with a powerful little formula:
The fallen distance = (1/2) × (gravity’s strength) × (time in seconds)²
Let’s unpack this:
Gravity’s strength (g): This is the rate at which Earth accelerates any object dropped towards it, a value of about 9.8 meters per second every second.
Time squared (t²): This is the heart of the matter. Because the stone’s speed is constantly growing, the distance it covers doesn’t just add up—it multiplies. In the first second, it falls a short distance. But by the second second, it is already moving much faster, so it covers a far greater distance in that same one-second interval.
The 1/2 in the formula isn’t arbitrary; it emerges naturally from the mathematics of how things move under constant acceleration. It’s the factor that perfectly balances the equation, accounting for the object’s starting speed of zero.
So, the stone’s journey downward is one of explosive growth in distance. If it takes twice as long to fall, it covers four times the distance. This squared relationship is the fundamental signature of free fall, a direct consequence of gravity’s unceasing and uniform pull.
Question 16.
A body is thrown vertically upwards with an initial velocity u. Write the expression for the maximum height attained by the body.
Ans:
When a body is thrown vertically upwards, its upward journey is a constant battle against gravity. The maximum height is the point where the body’s initial upward drive is completely exhausted by gravity’s pull.
We can find this height using a key principle of motion that connects velocity, acceleration, and distance, without needing the time of travel. The principle is:
v² = u² + 2as
Where:
- v is the final velocity.
- u is the initial velocity.
- a is the acceleration.
- s is the distance traveled.
Let’s apply this to the body’s upward flight:
- At the very peak of its height, for a single moment, the body comes to a stop. Therefore, its final velocity, v = 0.
- The body started with an initial velocity, u.
- The body is moving against the constant pull of gravity. This means the acceleration works to oppose its motion. So, the acceleration is a = -g (where ‘g’ is the acceleration due to gravity, approximately 9.8 m/s²).
- The distance traveled in this case is the maximum height, which we will call h.
Substituting these values into our equation:
(0)² = (u)² + 2(-g)(h)
This simplifies to:
0 = u² – 2gh
Finally, rearranging this equation to solve for the height (h), we get the expression:
h = u² / (2g)
This is the expression for the maximum height attained by a body thrown vertically upwards with an initial velocity u.
Question 17.
Define the terms mass and weight.
Ans:
Mass refers to the fundamental amount of substance, or matter, an object contains. Think of it as a numerical value for the total number and type of atoms that make up the object. Its most important feature is that it is an inherent and constant property; it does not change regardless of where the object is located in the universe. The mass of an object directly determines its resistance to being accelerated—this is called inertia. A higher mass means it is harder to speed up or slow down. Its standard unit is the kilogram (kg).
Weight, in contrast, is not a property of the object itself, but rather a measurement of the gravitational force exerted on it. It is the force with which a planet or other massive body pulls the object toward its center. Since it is a force, its value is not constant—it changes based on the strength of gravity. An object weighs less on the Moon than on Earth because the Moon’s gravitational pull is weaker. The standard unit of weight is the Newton (N).
In essence, your mass is the same whether you are on Earth, in space, or on Mars. It defines what you are made of. Your weight is a measure of the pull of gravity on that mass, and it changes with location. Mass is the measure of matter, while weight is the measure of a force.
Question 18.
Distinguish between mass and weight.
Ans:
Think of mass as your fundamental cosmic inventory—it’s the total amount of “stuff” or matter you’re made of. It counts the protons, neutrons, and electrons in your body. This quantity is a fixed part of your identity; whether you are on Earth, floating on the Moon, or drifting in deep space, your mass remains the same. We measure this intrinsic property by its resistance to being moved, its inertia. A larger mass requires a stronger push to get it going or to stop it. We typically measure mass using a balance scale that compares it to a known standard.
Weight, on the other hand, is not about what you are, but about what is happening to you. It is a force—specifically, the force of gravity pulling on your mass. It tells you how heavy you feel in a specific location. Since it depends on gravity, which changes from planet to planet, your weight is variable. On the Moon, where gravity is weaker, your weight is less because the pull on your mass is gentler. In outer space, far from any gravitational source, your weight becomes zero (you are weightless), even though your mass hasn’t changed at all. We measure this force using a spring scale, which gauges the pull of gravity.
In essence:
- Mass is the “what.” It’s your constant, unchanging amount of matter.
- Weight is the “how much pull.” It’s the variable gravitational force acting on that matter.
The two are connected by a simple relationship: Weight = Mass x Gravity. Your mass is the constant in that equation, while gravity is the variable that determines your ever-changing weight.
Question 19.
State the S.I. units of (a) mass and (b) weight.
Ans:
We measure the physical world in specific, fundamental units. For mass and weight, these units are different because they describe two distinct concepts.
Mass refers to the sheer amount of substance an object contains. It is a measure of its inherent inertia—its resistance to changing its motion. The official unit for this fundamental quantity is the kilogram (kg). An object has the same mass everywhere, whether it’s on Earth, the Moon, or in deep space.
Weight, however, is not a measure of substance but of force. Specifically, it is the pull of gravity on an object’s mass. Because it is a force, its unit is the newton (N). One newton is defined as the force needed to accelerate a one-kilogram mass at one meter per second squared.
This is why the units differ. The kilogram tells you what the object is made of, while the newton tells you how strongly gravity is acting on that material. Your mass remains constant, but your weight changes if you travel to a planet with a different gravitational strength.
Question 20.
The value of g at the centre of Earth is zero. What will be the weight of a body of mass m kg at the centre of the Earth?
Ans:
The weight of a body is not an inherent property of the object itself; it is the force exerted on it by gravity. We calculate it as the product of the object’s mass (m) and the gravitational acceleration (g) at that specific location, expressed as W = m × g.
We are told that at the very center of the Earth, the value of g is zero. Physically, this occurs because the mass of the Earth surrounds the center point equally in all directions. These gravitational pulls from all sides cancel each other out perfectly, resulting in a net gravitational acceleration of zero.
If we place a body of mass m kg at this point, we simply substitute the values into the weight formula:
Weight (W) = m × g = m × 0
Therefore, the weight of the body at the Earth’s centre is zero newtons.
The object still has its mass (m kg), which is a measure of the matter it contains. However, it experiences no gravitational pull, so it is weightless. It would float effortlessly at the very core of the planet.
Question 21.
Which of the following quantities does not change by change of place of a body : mass or weight ?
Ans:
The quantity that does not change is the mass of the body.
Here is the simple reason why:
Mass is a fundamental measure of the total amount of matter, or “stuff,” inside an object. It is an intrinsic property. Whether the body is on Earth, on the Moon, or in the depths of space, the number and type of atoms that make it up remain constant. Therefore, its mass stays the same.
Weight, on the other hand, is fundamentally different. It is not a measure of “stuff,” but a measure of the force of gravity pulling on that stuff. This force changes depending on where you are in the universe because the strength of gravity differs.
- On Earth, the gravity is strong, so you have a certain weight.
- On the Moon, where gravity is about one-sixth of Earth’s, you would weigh only one-sixth of your Earthly weight.
- In outer space, far from any planet, your weight would be virtually zero because the gravitational pull is negligible.
Question 22.
Explain the meaning of the following statement ‘1 kgf = 9.8 N’.
Ans:
Think of the statement ‘1 kgf = 9.8 N’ as a simple unit conversion, like saying ‘1 foot = 12 inches,’ but for force instead of distance.
It defines the relationship between two different ways of measuring force.
- 1 kgf (Kilogram-Force): This is a unit of force based on a very familiar idea: weight. By definition, 1 kilogram-force is the weight of a 1-kilogram mass under the pull of Earth’s gravity. It’s a measure of how hard Earth pulls on that object.
- 9.8 N (Newtons): This is the standard international unit of force. A Newton is defined as the force needed to accelerate a 1-kilogram mass at a rate of 1 meter per second every second.
So, what does the equation tell us?
It reveals a key fact: the gravitational pull of the Earth on a 1-kilogram object is strong enough to accelerate it at 9.8 meters per second every second.
In essence, the statement is a bridge. It connects the everyday, practical concept of “weight” (kilogram-force) with the precise, scientific language of physics (Newtons). It confirms that the force we feel as the weight of a 1-kg bag of sugar is identical to a force of 9.8 Newtons.
You could say it’s the “exchange rate” between the language of the marketplace and the language of the physics lab. If a force is measured as 1 kgf on Earth, you know its exact scientific value is 9.8 N.
Exercise 3 (E)
Question 1.
The gravitational force between two bodies is :
- Always repulsive
- always attractive
- attractive only at large distance
- Repulsive only at large distances .
Question 2.
The value of G is :
- 9.8 N m2 kg-2
- 6.7 x 10-11 N m2 kg-2
- 6.7 x 10-11 m s-2
- 6.7 N kg-1
Question 3.
The force of attraction between two masses each of 1 kg kept at a separation of 1 m is :
- 9.8 N
- 6.7 N
- 980 N
- 6.7 × 10-11 N
Question 4.
A body is projected vertically upward with an initial velocity u . If acceleration due to gravity is g , the time for which it remains in air , is :
- 𝑢 / 𝑔
- ug
- 2𝑢 / 𝑔
- 𝑢 / 2𝑔
Question 5.
An object falling freely from rest reaches ground in 2 s. If acceleration due to gravity is 9.8 m s-2, then the velocity of object on reaching the ground will be
- 9.8 m s-1
- 4.9 m s-1
- 19.6 m s-1
- Zero
Exercise 3 (E)
Question 1.
The force of attraction between two bodies at a certain separation is 10 N. What will be the force of attraction between them if the separation is reduced to half?
Ans:
The strength of the attraction between two objects is deeply tied to how far apart they are. The rule governing this is called the inverse-square law. This principle means that the force is inversely proportional to the square of the distance separating them.
If you start with a force of 10 N at a specific distance, and then you move the objects to half of that original distance, the calculation for the new force is straightforward.
Halving the distance means the new separation is 1/2 of the original. According to the law, we take the square of this fraction: (1/2)², which equals 1/4.
Since the force is inversely related to this value, it becomes proportional to 1 / (1/4), which is 4. The force therefore becomes four times stronger than it was initially.
A starting force of 10 N, when multiplied by this factor of 4, gives a new attractive force of 40 N.
Question 2.
Write the approximate weight of a body of mass 5 kg. What assumption have you made?
Ans:
To find the weight of a 5 kg object, we are essentially measuring the strength of the gravitational pull between that object and the planet it rests on. While we commonly refer to this as “weight” in daily life, in physics, it is the specific force of gravity acting on a mass.
The calculation requires knowing how strongly the local environment tugs on objects. On the surface of our planet, gravity causes objects to speed up by about 9.8 meters per second with each passing second—a value known as gravitational acceleration.
We determine the gravitational force, which is the object’s weight, through a simple multiplication:
Mass of the object × Gravitational acceleration
So, for our 5 kg object on Earth, the math is:
5 kg × 9.8 m/s² = 49 Newtons.
This result, 49 Newtons, is the actual measure of the downward force the object exerts due to gravity. If you were to place it on a scale, this is the force the scale would register.
It’s vital to remember that this number is tied to Earth. The object’s mass—the amount of substance it contains—remains a constant 5 kg everywhere. However, its weight is a product of its mass and the local gravitational field. On a world with weaker gravity, like the Moon, the same 5 kg object would feel noticeably lighter and register a smaller force on a scale, because the planetary pull acting upon it is less.
Question 3.
Calculate the weight of a body of mass 10 kg in (a) kgf and (b) newton. Take g = 9.8 m s-2.
Ans:
The weight of a body is calculated using the formula: Weight = mass × acceleration due to gravity (g).
Given:
- Mass = 10 kg
- g = 9.8 m/s²
(a) Weight in kilogram-force (kgf):
By definition, 1 kgf is the weight of a 1 kg mass under standard gravity (g = 9.8 m/s²). Therefore, for a mass of 10 kg, the weight in kgf is numerically equal to the mass.
Weight = 10 kgf.
(b) Weight in newton (N):
The weight of the body is 10 kgf or 98 N.
Question 4.
State the magnitude and direction of the force of gravity acting on the body of mass 5 kg. Take g = 9.8 m s-2.
Ans:
A steady, unseen hand constantly pulls an object weighing 5 kilograms toward the Earth. We can measure the strength of this pull, which amounts to 49 Newtons.
This value comes from a simple relationship: an object’s weight is the product of its mass and the local gravitational acceleration. For a 5 kg object, this is 5 kg multiplied by 9.8 meters per second every second, resulting in the 49 Newton force we feel as weight.
This pull has a single, unwavering direction: downward, following a path that leads directly toward the planet’s core. It is a persistent force, acting upon the object at every moment, whether it sits peacefully on a table or plummets through the air.
Question 5.
The weight of a body is 2.0 N. What is the mass of the body? (g = 10 m s-2)
Ans:
We know that the weight of an object is the force of gravity acting on it. The relationship is given by:
Weight (W) = mass (m) × acceleration due to gravity (g)
Or, written as a formula:
W = m × g
In this problem:
- Weight (W) = 2.0 N
- Acceleration due to gravity (g) = 10 m/s²
To find the mass (m), we rearrange the formula:
m = W / g
Now, we substitute the given values:
m = 2.0 N / 10 m/s²
Performing the calculation:
m = 0.2 kg
Therefore, the mass of the body is 0.2 kilograms. The unit changes from Newtons (N) to kilograms (kg) because 1 Newton is defined as 1 kg·m/s².
Question 6.
The weight of a body on Earth is 98 N, where acceleration due to gravity is 9.8 m s-2. What will be its (a) mass and (b) weight on the Moon, where acceleration due to gravity is 1.6 m s-2?
Ans:

Question 7.
A man weighs 600 N on the Earth. What would be his approximate weight on the Moon? Give a reason for your answer?
Ans:
A man who weighs 600 N on Earth would feel significantly lighter on the Moon, weighing approximately 100 Newtons.
The reason for this dramatic difference lies not in the man himself, but in the strength of the Moon’s gravity.
Weight is not an inherent property of an object; it is the measure of the gravitational pull acting on it. The man has a certain amount of matter, or mass, which remains constant everywhere. However, the force that the Moon exerts on that mass is much weaker than the Earth’s.
The Moon is far less massive than our planet. Because its gravitational pull is only about one-sixth as strong as Earth’s, it tugs on the man’s body with only one-sixth of the force.
Therefore, while Earth pulls him down with a force of 600 Newtons, the Moon would pull with a force of 600 N / 6 = 100 Newtons. He would be the same person, but the scale would show a much lower reading because the Moon’s gravitational grip is far more gentle. You would feel this as a remarkable sense of lightness, allowing you to take great, bounding leaps.
Question 8.
What is the (a) force of gravity and (b) weight of a block of mass 10.5 kg ? Take g = 10 ms-2 .
Ans:
Finding the pull of Earth’s gravity on an object—what we call its weight—is a simple calculation based on its mass.
We start with the known values for this specific block:
- Its mass, which is the amount of substance it contains, is 10.5 kilograms.
- The strength of Earth’s gravitational field, which determines how hard it pulls, is 10 meters per second squared.
The physical rule that connects these values is straightforward: the gravitational force (weight) is the result of multiplying the object’s mass by the local gravitational acceleration.
Performing this calculation gives us:
10.5 kg × 10 m/s² = 105 Newtons
It’s crucial to understand that in physics, an object’s weight is not separate from this gravitational force; they are one and the same. The number 105 Newtons isn’t just the force of gravity—it is the definitive measure of the block’s weight.
So, for this 10.5 kg block, the downward force of gravity and its weight on the scale are identical: 105 Newtons. They are two different names for the same measurable quantity.
Question 9.
(a)A ball is released from a height and it reaches the ground in 3 s. If g= 9.8 m s-2 Find : the height from which the ball was released
(b) A ball is released from a height and it reaches the ground in 3 s. If g= 9.8 m s-2 Find : the velocity with which the ball will strike the ground .
Ans:
Let’s work through the problem of the ball dropped from rest.
We know it starts with no initial speed (u = 0 m/s), falls for a duration of 3 seconds (t = 3 s), and is pulled down by gravity with an acceleration of 9.8 m/s² (g = 9.8 m/s²).
(a) Finding the Height
To find the distance the ball falls, we use the equation that connects initial velocity, time, and acceleration:
s = ut + (1/2)gt²
Plugging in our known values:
s = (0)(3) + (1/2)(9.8)(3)²
This simplifies to:
s = 0 + (1/2)(9.8)(9)
s = (1/2)(88.2)
s = 44.1 meters
Therefore, the ball was released from a height of 44.1 meters.
(b) Finding the Impact Velocity
To find the ball’s speed the moment before it hits the ground, we use the equation for final velocity:
v = u + gt
Plugging in our values:
v = 0 + (9.8)(3)
v = 29.4 m/s
Thus, the ball strikes the ground with a velocity of 29.4 m/s, directed straight downward.
44.1 \boxed{29.4}
Question 10.
What force, in newton, your muscles need to apply to hold a mass of 5 kg in your hand? State the assumption.
Ans:
To hold a 5 kg mass stationary in your hand, your muscles need to apply an upward force of approximately 49 Newtons.
Assumption: This calculation assumes you are on the surface of the Earth, where the acceleration due to gravity is a constant 9.8 m/s².
Reasoning:
The mass is pulled downward by the Earth’s gravity. The strength of this pull is its weight, calculated as:
Weight (Force) = Mass × Acceleration due to gravity
So, for a 5 kg mass:
Force = 5 kg × 9.8 m/s² = 49 Newtons.
Since the mass is held still and not accelerating, the net force on it must be zero. Therefore, your upward muscular force must perfectly balance the downward gravitational force. You are essentially pushing against the planet’s pull with exactly 49 N of force to keep the object in a state of equilibrium.
Question 11.
(a) A ball is thrown vertically upwards. It goes to a height of 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10 ms-2, find: the initial velocity of the ball.
(b) A ball is thrown vertically upwards. It goes to a height of 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10 ms-2 , find :
the final velocity of the ball on reaching the ground .
(c) A ball is thrown vertically upwards. It goes to a height of 20 m and then returns to the ground. Taking acceleration due to gravity g to be 10 ms-2 , find :
the total time of journey of the ball .
Ans:




Question 12.
A body is dropped from the top of a tower. It acquires a velocity 20 m s-1 on reaching the ground. Calculate the height of the tower. (Take g = 10 m s-2)
Ans:

Question 13.
(a) A ball is thrown vertically upwards. It returns 6 s later. Calculate the greatest height reached by the ball. (Take g = 10 m s−2)
(b) A ball is thrown vertically upwards. It returns 6 s later. Calculate : the initial velocity of the ball (Take g = 10 m s-2)
Ans:
(b): Uncovering the Launch Velocity
The beauty of this motion under gravity is its symmetry. The path upwards is a perfect mirror of the path downwards. Since the total time is 6 seconds, the ball must spend half that time rising and the other half falling. This means it takes 3 seconds to soar from your hand to its highest point, where it hangs in the air for just an instant.
At that peak moment, its velocity is zero. It has finished going up but has not yet begun to fall. We can now use a key relationship between velocity, time, and acceleration.
Gravity slows the ball down at a steady rate of 10 m/s every second. So, over the 3-second ascent, gravity works to completely erase the ball’s initial upward speed.
We can think of it like this:
The initial upward speed is drained away by gravity at 10 m/s each second. After 3 seconds, it’s gone.
Mathematically, this is: Initial Velocity = (Gravity’s pull) × (Time to reach the top)
So, Initial Velocity = (10 m/s²) × (3 s) = 30 m/s.
The ball left your hand at 30 meters per second.
(a): Finding the Peak Height
Now that we know the ball started at 30 m/s and slowed to a stop at the top over 3 seconds, we can find the distance it covered. For an object slowing down at a constant rate, the distance traveled is simply the average speed multiplied by the time.
Its speed dropped evenly from 30 m/s to 0 m/s. The average speed during the climb was (30 + 0) / 2 = 15 m/s.
If it moved at an average speed of 15 m/s for 3 seconds, the distance it rose is:
Height = (Average Speed) × (Time)
Height = (15 m/s) × (3 s) = 45 meters.
Therefore, the ball reached a maximum height of 45 meters above the point from which it was thrown.
Question 14.
A pebble is thrown vertically upwards with a speed of 20 m s-1. How high will it be after 2 s? (Take g = 10 m s-2)
Ans:

Question 15.
(a) How long will a stone take to fall to the ground from the top of a building 80 m high (b) What will be the velocity of the stone on reaching the ground? (Take g=10 m s-2)
Ans:
(a) Finding the Duration of the Fall
Since the stone starts from rest, its initial velocity is zero. It descends under the constant acceleration of gravity. The distance it covers is governed by the equation:
Distance = (Initial Velocity × Time) + (½ × Acceleration × Time²)
Plugging in our values:
- Distance (s) = 80 m
- Initial Velocity (u) = 0 m/s
- Acceleration (a) = 10 m/s²
The equation becomes:
80 = (0 × t) + (½ × 10 × t²)
80 = 5t²
Solving for time (t):
t² = 80 / 5 = 16
t = √16 = 4 seconds
Therefore, the stone takes 4 seconds to reach the ground.
(b) Finding the Speed upon Impact
The stone accelerates for 4 seconds before hitting the ground. Its final velocity can be found using the relationship between initial velocity, acceleration, and time:
Final Velocity = Initial Velocity + (Acceleration × Time)
Substituting the known values:
- Initial Velocity (u) = 0 m/s
- Acceleration (a) = 10 m/s²
- Time (t) = 4 s
The calculation is:
Final Velocity (v) = 0 + (10 × 4) = 40 m/s
We can verify this using an alternative method that relates velocity to distance:
(final velocity)² = (initial velocity)² + (2 × Acceleration × Distance)
v² = 0² + (2 × 10 × 80)
v² = 1600
v = √1600 = 40 m/s
Both methods confirm that the stone strikes the ground with a velocity of 40 m/s.
Question 16.
A body falls from the top of a building and reaches the ground 2.5 s later. How high is the building? (Take g = 9.8 m s-2)
Ans:
To find the height of the building, we analyze the object’s fall under the constant acceleration of gravity. The most suitable formula for this motion is derived from the equations of kinematics.
We know the object starts from rest, so its initial velocity is zero. The duration of the fall is 2.5 seconds, and gravity accelerates it downward at 9.8 m/s². The distance it covers is given by the expression:
s = (1/2)gt²
Where ‘s’ is the distance, ‘g’ is the acceleration due to gravity, and ‘t’ is the time. This formula works because the starting speed is zero, which simplifies the general equation.
Substituting our known values:
s = (1/2) * 9.8 * (2.5)²
The calculation proceeds by first determining the square of the time: 2.5 multiplied by itself gives 6.25.
We then multiply this result by the acceleration: 9.8 times 6.25 equals 61.25.
Finally, we take half of this product, as dictated by the formula: (1/2) * 61.25 gives a final result of 30.625.
Therefore, the object fell a vertical distance of 30.625 meters. This distance is equal to the height of the building from which it was dropped.
Question 17.
(a) A ball is thrown vertically upwards with an initial velocity of 49 m s-1 . calculate : the maximum height attained .
(b) ball is thrown vertically upwards with an initial velocity of 49 m s-1. Calculate: The time taken by it before it reaches the ground again. (Take g = 9.8 m s-2).
Ans:


Question 18.
A stone is dropped freely from the top of a tower and it reaches the ground in 4 s. Taking g = 10m s-2, calculate the height of the tower.
Ans:
To find the height of the tower, we can use the fundamental relationship for an object starting from rest and accelerating downwards.
We know the stone begins with zero initial velocity, falls for a duration of 4 seconds, and accelerates at 10 m/s².
The distance covered by such an object is given by the formula:
Distance = (1/2) × acceleration × (time)²
Plugging our known values directly into this relationship:
Height = (1/2) × (10 m/s²) × (4 s)²
First, we square the time: 4 s × 4 s = 16 s².
The calculation then becomes:
Height = (1/2) × 10 × 16
Height = 5 × 16
Height = 80 meters
Therefore, the height of the tower is 80 meters.
Question 19.
(a) A pebble is dropped freely in a well from its top. It takes 20 s for the pebble to reach the water surface in the well. Taking g = 10 m s-2 and speed of sound = 330 m s-1. Find : The depth of water surface
(b) A pebble is dropped freely in a well from its top. It takes 20 s for the pebble to reach the water surface in the well. Taking g = 10 m s-2 and speed of sound = 330 m s-1. Find : The time when echo is heard after the pebble is dropped.
Ans:
Part 1: Finding the Depth of the Well
We know it takes 20 seconds for the pebble to fall from the top to the bottom. Assuming it falls freely under gravity (with an acceleration of 10 m/s²), we use the law of motion for an object starting from rest:
The distance fallen is equal to (1/2) × acceleration × (time)².
Plugging in the numbers:
Depth = (1/2) × 10 × (20)²
This simplifies to:
Depth = 5 × 400
Depth = 2000 meters.
So, the well is 2000 meters deep.
Part 2: Finding When the Echo is Heard
The “plunk” sound of the impact has to travel back up the 2000-meter well to reach the listener’s ears. Sound doesn’t fall; it travels at a more or less constant speed. We’ll use a standard speed of 330 meters per second for sound in air.
The time needed for the sound to travel up is:
Time_sound = Distance / Speed = 2000 / 330 seconds.
We can simplify this fraction by dividing the top and bottom by 10:
Time_sound = 200 / 33 seconds.
The total time the person experiences is the sum of the falling time and the sound’s return time:
Total Time = Time_fall + Time_sound
Total Time = 20 + (200 / 33) seconds.
To add these, we convert 20 into a fraction with the same denominator (33):
20 = (20 × 33) / 33 = 660 / 33.
Now we add:
Total Time = (660 / 33) + (200 / 33) = (660 + 200) / 33 = 860 / 33 seconds.
Therefore, the listener hears the echo 860/33 seconds, or approximately 26.06 seconds, after dropping the pebble.
Final Answers:
- Depth of the well: 2000 m
- Time when the echo is heard: 860/33 s
Question 20.
A ball is thrown vertically upwards from the top of a tower with an initial velocity of 19.6 m s-1. The ball reaches the ground after 5 s. Calculate: (i) The height of the tower, (ii) The velocity of the ball on reaching the ground. Take g= 9.8 ms-2.
Ans: